

Пример расчета характеристик вычислительных систем на основе стохастических сетей

В данном примере показан расчет характеристик двух вычислительных систем. Одну систему можно представить разомкнутой стохастической сетью, а другую - замкнутой.

Расчет характеристик разомкнутых стохастических сетей

Исходными данными для расчета являются следующие параметры:

 количество систем в сети:	n=4;
 количество каналов в каждой системе:	K1=1, K2=1, K3=1, K4=4;
 средняя длительность обслуживания заявок в каждой системе:	1=0,4 с, 2=0,2 с, 3=0,15 с, 4=0,1 с;
 вероятности переходов заявок Рij из системы Si в систему Sj стохастической сети:	P10=0,1, P12=0,27, P13=0,29, P14=0,34;
 интенсивность входного потока заявок:	0=0,1 с-1.

Рассчитаем характеристики вычислительной системы, моделью которой является разомкнутая стохастическая сеть (см. рис. 3.2).

Порядок циркуляции заявок в этой сети отображается с помощью графа передач (см. рис. 3.3).

На основании данных вероятностей переходов составим матрицу переходов P:

По матрице вероятностей определим интенсивность потоков, входящих в системы S_i.

₀=0,1₁  0,1=0,1₁  ₁=1 c^-1 =>

₁=₀+₂+₃+₄ ₂=0,27 c^-1





₂=0,27₁ ₃=0,29 c^-1

₃=0,29₁ ₄=0,34 c^-1

₄=0,34₁

Теперь найдем коэффициенты передачи для каждой из систем

;

;

;

.

В рассматриваемой сети существует стационарный режим, так как выполняется условие (3.4): , т.е.

.

Загрузка систем S₁, S₂, S₃ и среднее число занятых каналов в системе S₄ равны соответственно

Для данной стохастической сети подтверждается существование стационарного режима, поскольку все полученные значения _i<1.

Подставляя полученные значения в (3.8) и учитывая, что K₁=K₂=K₃=1 и K₄=4, определим вероятности простоя систем сети:

₀₁=(1-₁)=0,6;

₀₂=(1-₂)=0,946;

₀₃=(1-₃)=0,955;

Верхний индекс значения означает степень K_i величины _i.

Теперь, используя (3.9)-(3.12) и полученные значения _i и _0i, определим все характеристики систем S_i в сети:

 средняя длина очереди

;

;

;

;

.

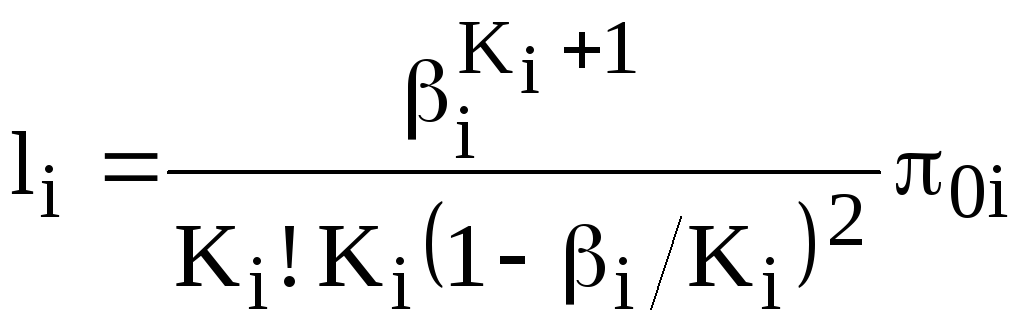 среднее число заявок в системе

mi= li+i;

m1=0,666;

m2=0,05708;

m3=0,04547;

m4=0,034.

 среднее время ожидания заявки в очереди

i=li/i;

1=0,266 с;

2=0,0114 с;

3=0,0068 с;

4 => 0 с.

 среднее время пребывания заявки в системе

ui=mi/i;

u1=0,666 c;

u2=0,2114 c;

u3=0,1567 c;

u4=0,1 c.

Подставляя значения l_i, m_i, _i, u_i в (3.13)-(3.16) и учитывая среднее число попаданий заявок в системы сети a_i, определим характеристики сети в целом:

 среднее число заявок, ожидающих обслуживания в сети

;

 среднее число заявок, пребывающих в сети

;

 среднее время ожидания заявки в сети

;

 среднее время пребывания заявки в сети

.