3.3.3. Квантроны

Существует два способа использования джозефсоновских элементов в цифровых устройствах в ячейках логики и памяти вычислительных систем. При обоих способах единица информации организуется в виде тока в сверхпроводящем контуре, джозефсоновские элементы используются для управления этими токами их генерации, переключения, уничтожения. Отличие способов состоит лишь в величине магнитного потока, находящегося в сверхпроводниковом контуре.

Если единица информации запоминается током Iв контуре с индуктивностьюLтак, чтоLI>>Ф₀, гдеФ₀– квант магнитного потока, эффект квантования практически не сказывается на работе устройства. При этом управляющие элементы называют криотронами, такие элементы мы рассматривали в предыдущих разделах (п.п. 3.3.1, 3.3.2).

Если LI ≈ Ф₀, единицы информации записываютсяодиночными квантамимагнитного потока, что вызывает принципиальные изменения в построении цифровых устройств. Все устройства на одиночных квантах магнитного потока можно разбить на две группы: устройства надискретныхджозефсоновских переходах и устройства нараспределенныхпереходах. Здесь мы рассмотрим особенности работы устройств первой группы, поскольку в технологии создания однородных качественных ВТСП распределенных переходов сегодня имеются нерешенные проблемы.

В устройствах на дискретных переходах используется эффект квантования магнитного потока (п. 1.2). Наиболее простая конфигурация, в которой наблюдается это явление, представляет собой кольцо из сверхпроводящего материала, в которое включен джозефсоновский переход. Максимальноеколичество квантов потока, которое может содержаться в кольце, определяется величиной критического тока контактаI_С0и индуктивностью кольцаL:

N=I_С0L/Ф₀. (3.22)

Очевидно, что такое кольцо может находиться в (2N+1) состояниях. Именно эти состояния кольца с током и могут использоваться для хранения информации.

Удобным для практической реализации является универсальный переключательный элемент, получивший название параметрический квантрон (рис. 3.11, а).

а) б)

Рис. 3.11. Параметрический квантрон: а – эквивалентная схема; б – зависимость полного магнитного потока от внешнего потока

Квантрон представляет собой кольцо из сверхпроводящего материала 1 замкнутое, управляемым джозефсоновским переходом – криотроном 2. С кольцом гальванически или индуктивно связаны шина смещения 3, шины записи и считывания 4. Квантрон работает следующим образом. По шине смещения пропускают ток такой величины, чтобы его магнитный поток Ф_см сместил состояние равновесия в точку Ф₀/2 (рис. 3.11, в). Как видно из рисунка, это состояние может быть устойчивым при I_С0=I_{С0 min} (кривая 1) или неустойчивым при I_С0=I_{С0 max} (кривая 2). Направление тока в контуре будет определяться знаком дополнительного потока ΔФ, вызванного, например токами, текущими в соседних контурах гальванически или индуктивно связанных с данным контуром. Таким образом, можно осуществить запись в контур состояния, соответствующую знаку ΔФ, т.е. элемент осуществляет мажоритарную функцию. На этом элементе можно реализовать любые логические функции. Существенным является то, что в рассмотренном квантроне критический ток может быть весьма малым (10 мкА). Это вызвано тем, что в данном случае не требуется большого коэффициента усиления.

Одним из вариантов квантронас расширенными функциональными возможностями является логический элемент, содержащий дополнительный джозефсоновский переход в контуре, с которым связана дополнительная шина управления (рис. 3.12).

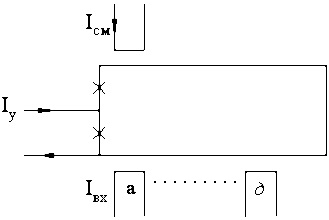
Рис. 3.12. Инжекционный квантрон

Поскольку шина управления связана с контуром гальванически, ток управления вводится в контур непосредственно т.е. инжектируется. Поэтому рассматриваемый квантрон можно назвать инжекционным квантроном. Гальваническая связь, в отличие от индуктивной, позволяет осуществить связь с контуром малых размеров. Кроме того, гальваническая связь позволяет создать шины управления и сам сверхпроводящий контур в одном слое, что заметно упрощает технологию изготовления таких элементов.

Рассмотренные элементы с параметрическим управлением обладают минимальной энергией переключения, ограниченной лишь квантовыми эффектами.