задания по математике / лекции / аналитика

Тема №1 Аналитическая геометрия на плоскости

Задача 1. Даны вершины треугольника : (-4;8), (5;-4), (10;6).

Найти:

1) длину стороны ;

2) уравнения сторон и и их угловые коэффициенты;

3) внутренний угол ;

4) уравнение высоты и ее длину;

5) уравнение окружности, для которой высота есть диаметр.

Решение:

1) Расстояние между точками и определяется по формуле:

(1)

Подставив в эту формулу координаты точек и , имеем:

.

2) Уравнение прямой, проходящей через точки и , имеет вид:

(2)

Подставив в (2) координаты точек и , получим

8

уравнение прямой :

Для нахождения углового коэффициента прямой разрешим полученное уравнение относительно .

: . Отсюда . Подставив в формулу (2) координаты точек и , найдем уравнение прямой :

Отсюда

3) Угол между двумя прямыми, угловые коэффициенты которых равны и , определяется по формуле:

(3)

Угол, образованный прямыми и , найдем по формуле (3), подставив в нее

9

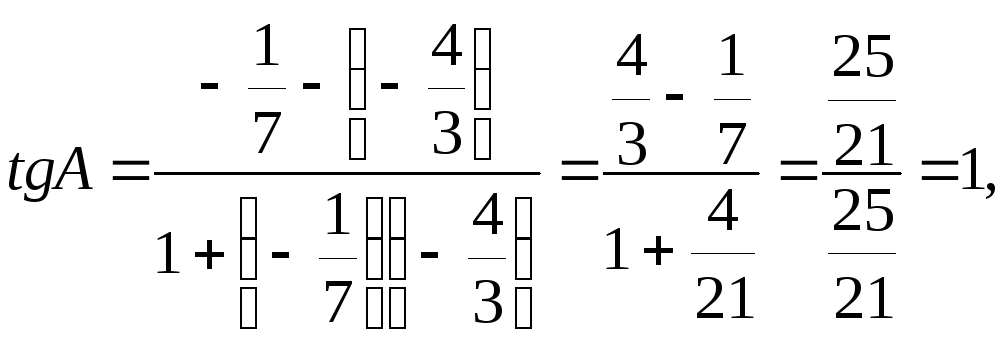
4) Так как высота перпендикулярна стороне , то угловые коэффициенты этих прямых обратны по величине и противоположны по знаку, т.е.

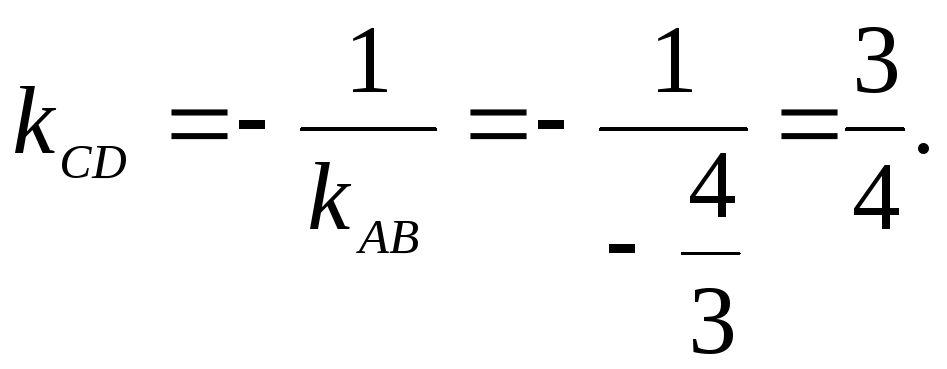
Уравнение прямой, проходящей через данную точку в заданном угловым коэффициентом направлении, имеет вид:

(4)

Подставив в (4) координаты точки и , получим уравнение высоты :

Для нахождения длины определим координаты точки , решив систему уравнений и :

10

откуда то есть

Подставив в формулу (1) координаты точек и , находим:

.

5) Уравнение окружности радиуса с центром в точке имеет вид:

(5)

Так как является диаметром искомой окружности, то ее центр есть середина отрезка . Воспользовавшись формулами деления отрезка пополам, получим:

Следовательно, и .

Используя формулу (5), получаем уравнение искомой окружности:

11

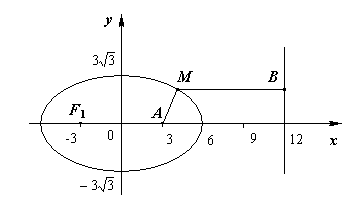
Задача 2. Составить уравнение линии:

Пример1

для каждой точки которой ее расстояние до точки равно расстоянию до прямой . Полученное уравнение привести к простейшему (каноническому) виду и построить кривую.

Рис. 1 Парабола

Решение. - текущая точка искомой кривой.

Опустим из точки перпендикуляр на прямую (рис. 1). Тогда .

12

Так как , то

или

Полученное уравнение определяет параболу с вершиной в точке . Для приведения уравнения параболы к простейшему (каноническому) виду положим . Тогда в системе координат уравнение параболы принимает следующий вид: . В системе координат строим параболу.

Пример2

для каждой точки которой отношение расстояний до точки и до прямой равно числу . Полученное уравнение привести к простейшему (каноническому) виду и построить кривую.

13

Рис. 2 Эллипс

Решение. Пусть - текущая (произвольная) точка искомого геометрического множества точек.

Опустим перпендикуляр на прямую (рис.2). Тогда .

По условию задачи .

Тогда

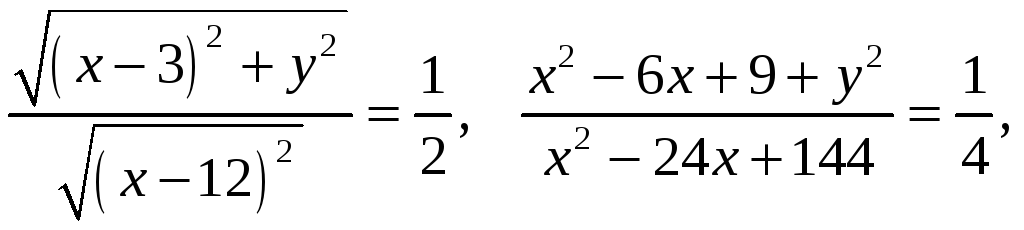
14

Полученное уравнение представляет собой эллипс вида где

Определим фокусы эллипса и . Для эллипса справедливо равенство Таким образом, и - фокусы эллипса (точки и совпадают).

Эксцентриситет эллипса

Тема 2. Векторная алгебра и аналитическая геометрия в пространстве

Задача 3. Даны координаты четырех точек . Требуется:

1. записать векторы 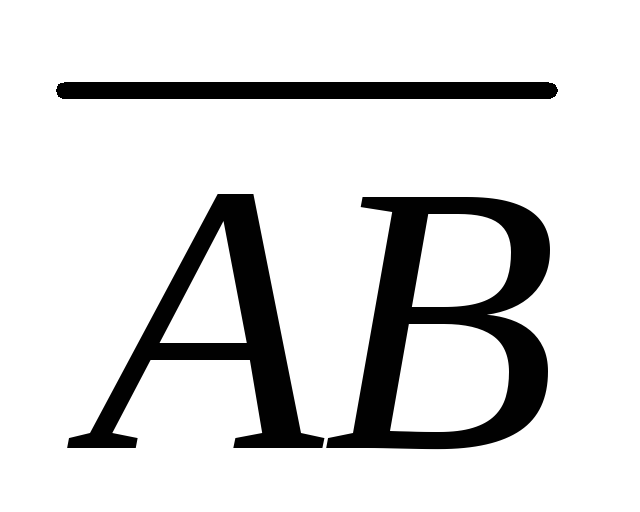и в системе орт и найти модули (длины) этих векторов;

2. найти угол между векторами 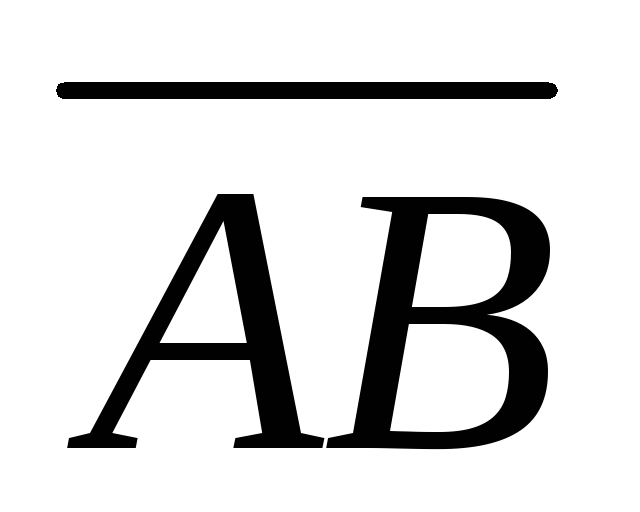и ;

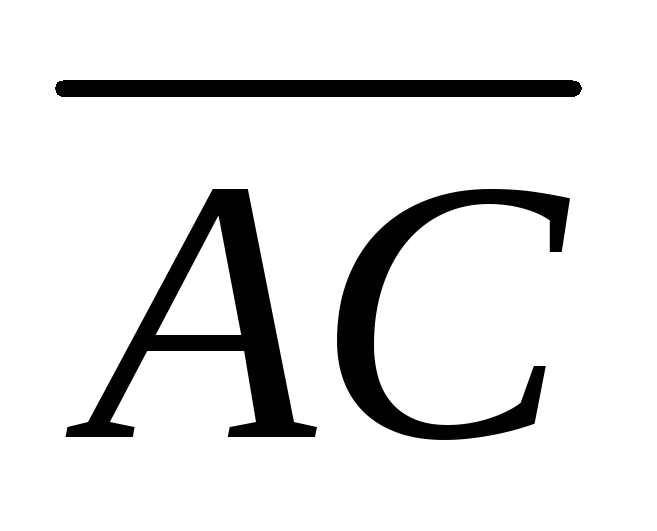3. найти проекцию вектора на направление вектора ;

4. вычислить площадь ;

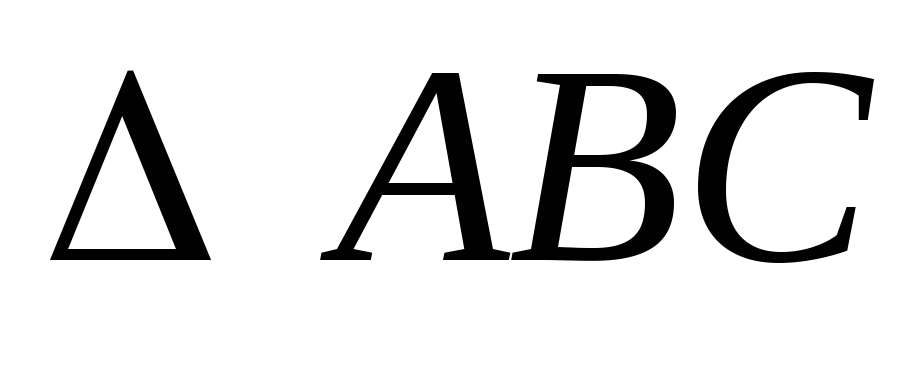5. вычислить объем пирамиды ;

6. составить уравнение плоскости, проходящей через точку перпендикулярно вектору ;

7. найти расстояние от точки до найденной плоскости.

15

Решение.

1) Для двух заданных точек и вектор через орты выражается следующим образом:

(1)

Подставляя в эту формулу координаты точек и , имеем:

.

Подобным образом

.

Модуль вектора вычисляется по формуле

. (2)

Подставляя в формулу (2) найденные ранее координаты векторов и , находим их модули:

2) Косинус угла , образованного векторами и , равен их скалярному произведению, деленному на произведение их модулей:

(3)

Так как скалярное произведение двух векторов, заданных своими координатами, равно сумме попарных

16

произведений одноименных координат, то

Применяя формулу (3), имеем:

3) Проекция вектора на направление вектора можно найти по следующей формуле:

Таким образом, , учитывая , получаем

4) Площадь треугольника, построенного на двух векторах, равен модуля векторного произведения векторов:

Векторное произведение векторов и вычисляется по формуле:

17

Отсюда имеем

Найдем модуль (длину) полученного вектора:

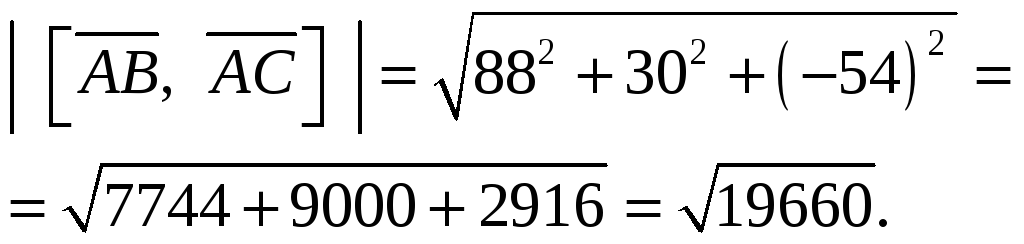
Площадь искомого треугольника:

5) Объем пирамиды, построенной на трех векторах равен модуля смешанного произведения данных векторов:

, .

Найдем

.

Смешанное произведение векторов: , и находится по формуле:

18

Найдем смешанное произведение векторов

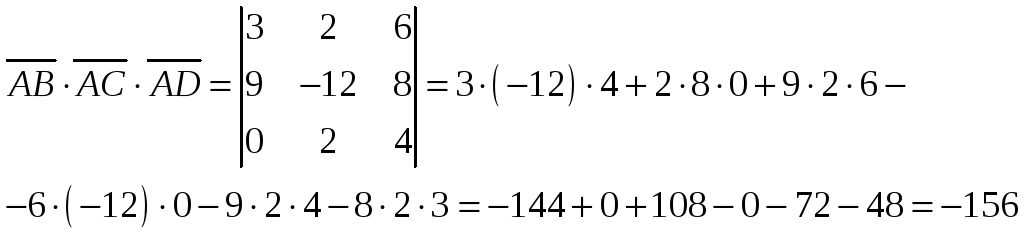
Объем пирамиды:

6) Известно, что уравнение искомой плоскости проходит через точку перпендикулярно вектору , имеет вид

(4)

По условию задачи искомая плоскость проходит через точку перпендикулярно . Подставляя в (4) , , получим:

- искомое уравнение плоскости.

8. Расстояние от точки 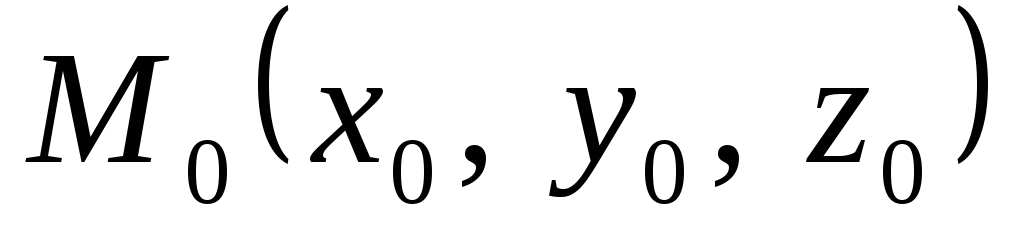до плоскости находится по формуле:

19

(5)

Используя формулу (5), найдем расстояние от точки до плоскости :