Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет геодезии и картографии

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

IDU / IDU_M1_L04

.pdf

Скачиваний:

Добавлен:

26.04.2015

Размер:

128.35 Кб

Скачать

☆

кафедра «Математическое моделирование» проф. П. Л. Иванков

Интегралы и дифференциальные уравнения

конспект лекций

для студентов 1-го курса 2-го семестра специальностей РЛ1,2,3,6, БМТ1,2

Лекция 4

Интегрирование выражений, рационально зависимых от тригонометрических функций. Интегрирование иррациональных функций. Примеры интегралов, не выражающихся через элементарные функции.

Через R(x, y, ..., t) будем обозначать рациональную функцию указанных аргументов (т.е. отношение двух многочленов от этих аргументов). Выше мы научились интегрировать рациональные функции. В дальнейшем основным приемом интегрирования функций различных классов будет применение таких подстановок, которые приводят подын-

тегральное выражение к рациональному виду.

Этот прием называется рационализацией

подынтегрального выражения.

Интеграл

R(sin x, cos x)dx

( )

подстановкой

u = tg

−π < x < π,

сводится к интегралу от рациональной функции.В самом деле,

2 sin x cos x

2 tg x

sin x =

cos2 x

+ sin2 x

1 + tg2 x

1 + u2

cos x =

cos2 x2 − sin2 x2

1 − tg2 x2

1 − u2

1 + tg2 x

1 + u2

cos2 x

+ sin2 x

x = 2 arctg u,

dx =

2du

следовательно,

1 + u2

1 − u2

R(sin x, cos x)dx = 2

1 + u2 1 + u2

1 + u2

Рассмотренная подстановка называется универсальной.

Пример. Применим универсальную подстановку для вычисления интеграла

I = Z

1 + 3 cos x

Имеем

1 − u2

−1

I =

1 + 3

2du

1 + u2

2 − u2

= 2√2 ln

√2 u

+ C = 2√2 ln

√

tg x2

+ C.

√

+ u

√

+ tg x

−

− 2

При вычислении интеграла (*) часто используют также

подстановки

u = cos x,

u = sin x, u = tg x.

В некоторых случаях применение этих подстановок оказывается более выгодным, чем применение универсальной подстановки. В качестве примера рассмотрим интеграл

Im,n = Z

cosm x · sinn xdx,

где

m и

n - целые числа.

Пусть сначала

n - нечетное число; тогда

Im,n = Z

cosm x · sinn−1 x · sin xdx = − Z

cosm x · (1 − cos2 x) n−2 1 d cos x =

= − Z

um(1 − u2) n−2 1 du,

где

u = cos x . Если нечетным является

m , то применяем подстановку

u = sin x . Если

m и

n являются четными,

то, поскольку

cos2 x =

sin2 x =

tg2 x

1 + tg2 x

можно применить подстановку u = tg x . В этом случае

x = arctg u,

dx =

, и мы

1 + u2

получаем, что

Im,n = Z

1 + u2

т.е.

дело сводится к интегрированию рациональной функции.

Если оба числа m и n

являются нечетными, то можно применить подстановку u = cos 2x .

В самом деле,

Im,n = Z (cos2 x) m2−1

· (sin2 x) n−2

· cos x · sin xdx =

1 + cos 2x

m−1

cos 2x

n−1

= −

1 −

d cos 2x =

m−1

1 − u

n−1

1 + u

du,

−4 Z

m − 1

n − 1

и получился интеграл от рациональной функции, т.к. показатели степени

являются целыми числами (быть может, отрицательными).

Пример.

Применим последний прием для вычисления интеграла

I9,7 = Z

cos9 x · sin7 xdx.

Имеем

(cos2 x)4

(sin2 x)3

cos x

sin xdx =

1 + u

1 − u

3 du =

−

4 Z

9,7

= −29

Z (1 + u)(1 − u2)3du = −512

Z (1 − u2)3du + Z

(1 − u2)3udu =

= −512

Z (1 − 3u2 + 3u4

− u6)du − 2

Z (1 − u2)3d(1 − u2) =

u2)4

= −

u − u3 +

u5 −

−

+ C,

u = cos 2x.

512

Интегралы

sin αx · cos βxdx,

sin αx · sin βxdx и

cos αx · cos βxdx

вычисляются с помощью формул элементарной тригонометрии:

sin αx · cos βx =

(sin(α + β)x + sin(α − β)x),

sin αx · sin βx =

(cos(α − β)x − cos(α + β)x),

cos αx · cos βx =

(cos(α + β)x + cos(α − β)x).

Например,
Z		1	Z		1	Z		1		1
	sin 2x · cos xdx =			sin 3xdx +			sin xdx = −		cos 3x −		cos x + C.
		2			2			6		2

Рассмотрим интегралы от некоторых иррациональных функций. Пусть требуется вычислить интеграл

I = Z

R x,

αx + β

, ...,

αx + β

dx, где

γx + δ

6= 0; r1, ..., rn − рациональные числа, m − их общий

наименьший знаменатель.

Пусть

αx + β

t =

;

γx + δ

тогда

x = r(t) =

δtm − β

;

dx = r0(t)dt,

и мы получаем, что

α − γtm

I = Z

R(r(t), tmr1 , ..., tmrn)r0(t)dt,

после чего дело сводится к интегрированию рациональной функции.

Пример. Пусть

I =

x + 1 .

+ 1 ·

−

Тогда, применяя указанную выше подстановку, получаем

− 1

(t4

− 1)2

x − 1

t = 4

x + 1

x =

+ 1

dx =

−8t3dt

;

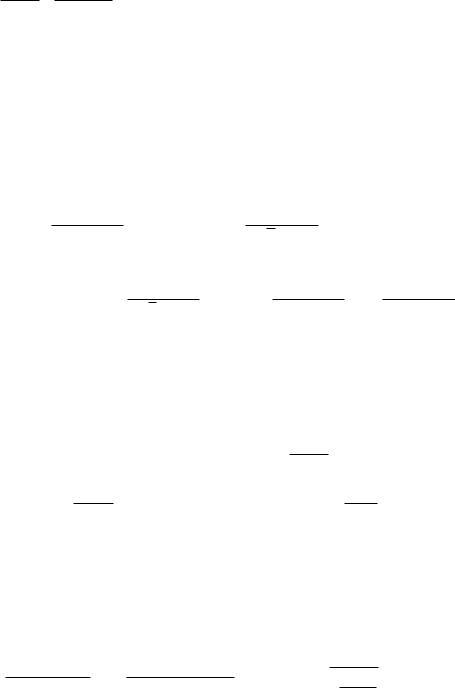
I = t

t4 − 1

−8t3dt

dt =

2t4

(t4 − 1)2

−

t4 − 1

−

Z t2 − 1

− t2 + 1

= ln

t + 1

+ 2 arctg t + C,

t = 4

x +

t − 1

x −

1 .

R	√
Рассмотрим теперь интегралы вида	R(x, ax2 + bx + c)dx ;разберем два случая.

Пусть сначала квадратный трехчлен

ax2 + bx + c

не имеет вещественных корней; в этом

случае

a > 0 , и имеет смысл подстановка

√

+ bx + c = t − a · x.

Тогда

ax2 + bx + c = t2 − 2√

· tx + ax2;

x =

2√

−· t + b

;

dx =

2√ta

−· t + b

dt;

R(x, √ax2 + bx + c)dx =

t − √a

2√ta

−t + b

;

2√

−t + b

2√

−t + b

dt,

и дело сводится к интегрированию рациональной функции. Рассмотренная подстановка является одной из подстановок Эйлера.

Пример. Пусть		I = Z		x√x2		+ 1 .
					dx
Применим подстановку Эйлера:	√
			= t − x,
		x2 + 1

x =	t2 − 1	,	dx =	t2 + 1	dt;
	t
				2t2

I =

t2 − 1

−1

t2 + 1

dt = 2

= ln

t − 1

+ C =

−

t + 1

−

x +

√x

+ 1

= ln

−

+ C.

√

x +

+ 1 + 1

Пусть теперь квадратный трехчлен ax2 + bx + c имеет два вещественных корня, т.е.

ax2 + bx + c = a(x − λ)(x − µ).

Тогда

√ax2 + bx + c = pa(x − λ)(x − µ) = |x − λ| · raxx −− µλ,

и мы имеем интеграл уже рассмотренного типа:

R(x,

√ax2 + bx + cdx = R

x, |x − λ| · r

dx.

−

Здесь рационализация достигается подстановкой

t = r

−− λ.

В заключении отметим, что многие интегралы от элементарных функций не выражаются через элементарные функции; таковы, например,встречающиеся в приложениях ин-

cos x2dx, Z

sin x2dx, Z

cos x

dx, Z

sin x

тегралы

e−x

dx,

и др.

ln x

Соседние файлы в папке IDU

#
26.04.2015118.65 Кб7IDU_M1_L01.pdf
#
26.04.2015122.67 Кб5IDU_M1_L02.pdf
#
26.04.2015122.41 Кб6IDU_M1_L03.pdf
#
26.04.2015128.35 Кб4IDU_M1_L04.pdf
#
26.04.2015179.56 Кб6IDU_M1_L05_06.pdf
#
26.04.2015133.27 Кб6IDU_M1_L07.pdf
#
26.04.2015157.37 Кб6IDU_M2_L08.pdf
#
26.04.2015141.56 Кб6IDU_M2_L09_10.pdf
#
26.04.2015155.9 Кб6IDU_M2_L11.pdf