
- •9.5. Допуски для функций
- •Оценка результатов наблюдений
- •Техника нахождения оценки
- •Вектор-функция случайного вектора
- •Вычисление значения оценки
- •9.3. Вес функции измеренных величин
- •9.4 Определение доверительного интервала для математического ожидания, дисперсии и стандарта функции случайного вектора
- •Доверительный интервал дисперсии (стандарта) функции
- •9.5. Допуски для функций
- •9.6 Оценка результатов наблюдений
- •9.6. А. Обработка равноточных измерений
- •9. 6.Б. Обработка прямых неравноточных измерений
- •9.5. В. Обработка неравноточных коррелированных измерений
Вектор-функция случайного вектора
Пример: при вычислении координат точек в системе снимка мы должны учесть влияние ошибок наблюдений координатных меток, а не только ошибок наблюдений точек. Отсчеты на координатные метки используются при вычислении координат и параллаксов всех точек снимка, значит, все вычисленные координаты х , у снимка (а для стереопары еще р и q) суть функции отсчетов Vx и Vу на точку и отсчетов +1, +2 +3 +4 на координатные метки, поэтому они будут коррелированны:

![]()
![]() Столбец
слева от знака равенства есть вектор
функций случайных величин. Для вектора
функций согласно (9.2) мы можем записать
вектор A,
состоящий из градиентов
Fi
Столбец
слева от знака равенства есть вектор
функций случайных величин. Для вектора
функций согласно (9.2) мы можем записать
вектор A,
состоящий из градиентов
Fi
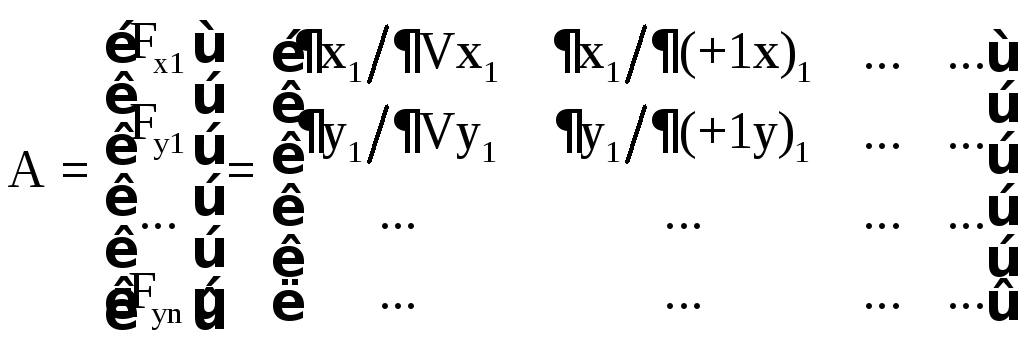 .
Образуется
матрица. Это матрица первых производных,
которую называют матрицей
Якоби (а
ее определитель
- якобиан).
Зная матрицу Якоби и ковариационную
матрицу Kx
случайного вектора
.
Образуется
матрица. Это матрица первых производных,
которую называют матрицей
Якоби (а
ее определитель
- якобиан).
Зная матрицу Якоби и ковариационную
матрицу Kx
случайного вектора
![]() ,
размер которой будет 2(n+4)
на 2(n+4),
мы вычисляем по (9.2) ковариационную
матрицу вектор-функции
,
размер которой будет 2(n+4)
на 2(n+4),
мы вычисляем по (9.2) ковариационную
матрицу вектор-функции
![]() ( 9.4)
.Для наглядности раскроем матрицы ( 9.4)
( 9.4)
.Для наглядности раскроем матрицы ( 9.4)

Запись для вектора функций в алгебраическом виде получается крайне сложной:
(f/x1)2 S12 +(f/x2)2S22+. . . +(f/xn)2Sn2 + . . . +2f/x1 f/x2 r12S1S2+. . .+2f/xn-1f/xnrn-1 nSn-1Sn (это частица формулы)
Формулы (9.2) или (9.3) служат для вычисления дисперсии функций случайного вектора, элементы которого коррелированны. Они действительны при рассмотренных выше условиях: (1) значение функции вычисляется не в особой точке функции, и (2) на рассматриваемом интервале функция близка к линейной.
Если
корреляция между элементами вектора Х
равна нулю, т.е. все
![]() ,
то ковариационная матрица KF
вырождается в диагональную, содержащую
только дисперсии или же, что то же самое,
корреляционная - в единичную. Тогда
выражение для вычисления дисперсии
функции ( 9.2) упрощается
,
то ковариационная матрица KF
вырождается в диагональную, содержащую
только дисперсии или же, что то же самое,
корреляционная - в единичную. Тогда
выражение для вычисления дисперсии
функции ( 9.2) упрощается
![]() .
(9.5) , а ковариационная матрица вектора
функций ( 9.4) –станет диагональной
.
(9.5) , а ковариационная матрица вектора
функций ( 9.4) –станет диагональной
![]() (9.6)
(9.6)
Вычисление значения оценки
Пользуясь
конкретными численными значениями
аргументов и параметров, входящих в
формулы, вычисляют численные значения
частных производных
![]() .
Если стандартSi
аргумента
xi
соизмерим с используемым значением
аргумента xi,
то следует подсчитать значение
соответствующих производных при
.
Если стандартSi
аргумента
xi
соизмерим с используемым значением
аргумента xi,
то следует подсчитать значение
соответствующих производных при
![]() ,
если данная величина находится в
числителе, и при
,
если данная величина находится в
числителе, и при
![]() ,
если в знаменателе, и сравнить с ранее
вычисленными. При отклонениях, более
10% от значения производной, в формулу
оценки дисперсии функции подставляют
большее значение производной.
,
если в знаменателе, и сравнить с ранее
вычисленными. При отклонениях, более
10% от значения производной, в формулу
оценки дисперсии функции подставляют
большее значение производной.
Числовой пример. (1) Оценка точности определения превышения по разности продольных параллаксов.
Высота
фотографирования H=
2100м
определена с СКО SH=
200 м,
продольный параллакс на снимке р
= 70 мм
измерен с СКО Sp=
1 мм,
а разность продольных параллаксов
р=
I мм
- с СКО Sp=
0.1 мм.
Находим превышение h=
2I00 1/70 = 30м.
Корреляция
отсутствует.
Вычисляем
![]() =
=
= 302 (I/I0.52+I/702+I/I02) = 8.I6 +0.I8 +9 = I7.34. Отсюда СКО определения превышения в 30 м будет Sh=√ I7.34= 4.16 м.
Так
как относительная ошибка![]() при этих данных постоянна, то меньшее
превышение определится точнее и наоборот.
при этих данных постоянна, то меньшее
превышение определится точнее и наоборот.
(2) Так, если при тех же условиях разность продольных параллаксов составит 10мм, что дает превышение в 300 м, а точность ее измерения о Sp остается та же самая, то превышение в 300 м определится с СКО = (8I6+18+9)1/2 = 8431/2=29м. Мы здесь не учли того, что высота фотографирования и продольный параллакс изменились: Н уменьшилась, а р увеличился. Предполагается пересчитать самостоятельно.
Сравнивая составляющие ошибки в примерах (1) и (2), видим, что во втором влияние ошибки определения высоты фотографирования является преобладающим.
Рассмотрим, каково будет ее влияние при H- SH =2100-200 м. (нижний предел, ибо Н в производной стоит в знаменателе). Влияние составит 99% общей ошибки, которая возросла на 10%, т.е. общее СКО - 32 м. Эту оценку принимаем за оценку СКО функции. Отметим, что в примере (1) влияние ошибки измерения продольного параллакса, а в (2) - еще и ошибки разности продольных параллаксов пренебрегаемо малы.
Общий вывод: для сохранения одной и той же абсолютной точности определения превышений, при больших превышениях местности нужно точнее определять все аргументы, служащие для вычисления его значения.
