10.3.1.2. Неравночисленные наблюдения в сериях

Постановка задачи в общем виде состоит в следующем.

Дано. Имеется m независимых нормально распределенных величин x_i, каждая из которых наблюдалась n_i раз. Всего имеется наблюдений. В результате получили выборкуx_ij из наблюдений, гдеi=1, 2,…, m; j=1,2, …, n_i.

Задача. Проверяется нулевая гипотеза H₀ , согласно которой центры распределения величин x_i равны, то есть . Предполагается, что все x_i выполнены с одним стандартом σ.

Решение.

Обозначим среднее арифметическое изi-й серии наблюдений

Средние каждой серии будут различаться вследствие как случайных погрешностей наблюдений, так и вследствие влияния исследуемого фактора. Для оценки значимости этого различия поступаем так.

Вычисляем общее среднее из наблюдений .

Находим общую эмпирическую дисперсию по известной формуле .

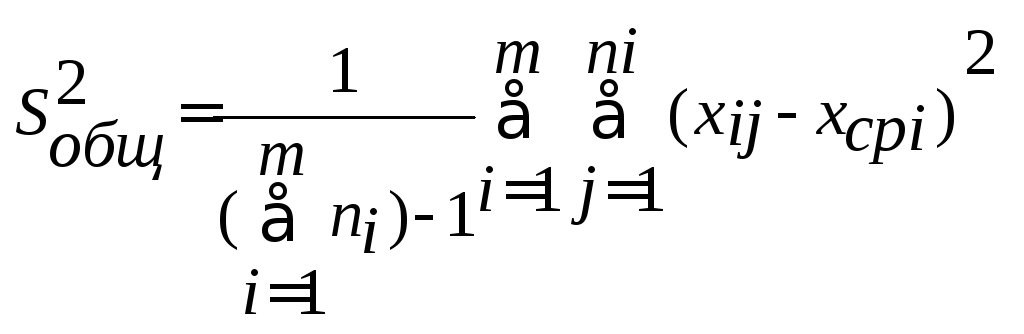Находим дисперсию, обусловленную влиянием фактора и дисперсию, какая остается после исключения влияния этого фактора.

Получим выражения для нахождения дисперсий: факторной и остаточной. Для этого разложим эту сумму в формуле общей дисперсии по частным средним:

Ниже написать

10.4. Технология проведения двухфакторного дисперсионного анализа

Задача анализа в том, чтобы выявить:

A. Существенно ли влияние некоторого фактора?

B. Если существенно, то какое изменение этого фактора можно признать несущественным?

	Ф	А	К	Т	О	Р		Вj	Средние xi
Ф	r\v	1	2	3	...	j	...	v	x1
А	1								x2
К	2								x3
Т	3
О	...
Р	i					xij		xiv	xi
	...
Аi	r					xrj		xrv	xr
средние xj		x1	x2	x3		xj		xv	x

1. Вычисляем: среднее в каждой j-ой строке , среднее в каждом i-ом столбце , а также общее среднее .

2. Вычисляем общую, факторные и остаточную дисперсии ,(дисперсия строк),(дисперсия столбцов),

3. Сравниваем дисперсии

А. Если, то факторы не влияют. Оценка дисперсии выборки будет, а ее доверительный интервал

B. Если , то фактор влияет. Тогда вычисляем отношения .

Затем по F-распределению, задаваясь доверительной вероятностью β, находим значения критерия по числам свободы меньшей и большей дисперсии.

Если , то влияние фактора существенно. Тогда оценка, а доверительный интервал этой оценки

Далее, при , делаем следующее.

4. Оцениваем меру систематической изменчивости.

если , то наблюдения неоднородные, имеется влияние фактора.

5. Группируем по оптимальным значениям факторов . Для этого

А. Определяем доверительные интервалы:

для строк А, состоящих из v столбцов (x_i - x_j )  t_qS_3ост(2/v),

для столбцов В, состоящих из r строк (x_i - x_j )  t_qS_3ост(2/r).

t_q определяем по распределению Стьюдента, задавая число степеней свободы (r-1)(v-1) и доверительную вероятность β.

t_q=1.96 для (r-1)(v-1)=36

Если разность двух значений попадает внутрь интервала, то она - несущественна, если вне интервала - существенна.

Б. Анализируем: сравниваем по фактору x_i с x_j. Попадает в вычисленный интервал –«+», вне интервала- «-».

Если x_j- отличается от всех, то- это брак ?x_посл

	1	2	3	4	5	6
1	+	-	-	+	-	+
2		+	-	+	-	+
3			+
4				+
5					+
6						+

Выводформулы оценки значимости расхождений. Нулевая гипотеза H_o: две выборки Х₁ и Х₂ объёмом n₁ и n₂ принадлежат одной и той же нормально распределённой совокупности N(x,²).

Решение для Х1	разность	Решение для Х2
	при r=0!
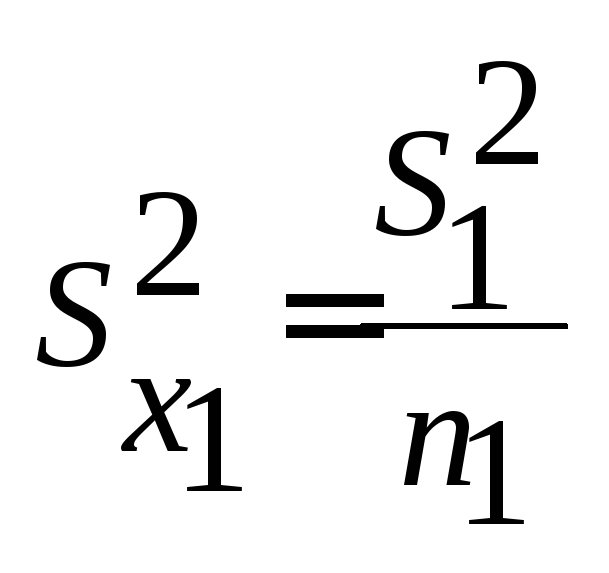
	некоррел.

Математическое ожидание расхождения .

Оценка его дисперсии .

ищем оценки выборочные, а не генеральной совокупности, т.е. по n₁ и по n₂ (а не (n₁-1) и (n₂-1)), то

, то .

Если выборки равны n₁=n₂=n, то 2n/n²=2/n и .

По доверительной вероятности  выбираем t=1, (или 1.5, или 2). В доверительный интервал попадают те пары, для которых выполняется условие.

Добавить формулы сделанные для компактных вычислений,( видимо в лекции старой).

7