7.2.4.3. Ортогональные полиномы Чебышева

При использовании обычных полиномов, степенных или тригонометрических, любое уточнение связи Y=P(X) величин X и Y , т.е. повышение степени полинома или увеличение числа гармоник, приводит к необходимости заново вычислять все коэффициенты, т.е. повторять все расчеты. Тaкоe уточнение называется регрессионный анализ.

Решение обычно выполняется по методу наименьших квадратов, что приводит к необходимости при каждом уточнении составлять и решать систему нормальных уравнений, порядок которой каждый раз увеличивается. Если необходимо сделать множество аппроксимаций, например, при отображении цифровой модели рельефа горизонталями, на процедуру требуется много времени. Для того чтобы упростить вычисления при подборе степени полинома согласно П.Л.Чебышеву представляют степенной полином

как сумму частных полиномов P₀,P₁,..P_k

, (7. 21)

степень j которых последовательно возрастает на единицу.

Тогда

. (7.22)

Коэффициенты b_ij подобраны так, что частные полиномы P_0, P₁,…, P_j ,… P_k образуют ортогональную систему.

Мы знаем, что скалярное произведение (P_i P_j) ортогональных векторов P_i и P_j равно нулю, а (P_i P_i ) и (P_j P_j) суть нормы этих векторов.

Рассмотрим, что это означает применительно к ортогональным полиномам.

Пусть сделано n наблюдений: при каждом фиксированном значении x_i измерено значение y_i со случайным отклонением d_i . Количество наблюдений n превышает степень k аппроксимирующего полинома P(x). Ибо в противном случае мы получаем однозначное соответствие между x и y: все случайные отклонения будут учтены коэффициентами полинома.

Для каждой пары совокупных измерений (x,y) мы можем записать линейное уравнение (7.22), в котором P_j будут коэффициентами, а искомыми неизвестными коэффициенты a_j при этих полиномах:

, (7.23)

где полиномы P_j составляют соответственно по значениям x₁ для первого уравнения, x₂ для второго, x_n для последнего.

Здесь количество уравнений n больше числа неизвестных k. Вследствие уклонений случайной величины y система не совместна.

Для получения оптимального псевдорешения переходим к системе нормальных уравнений (гл. II):

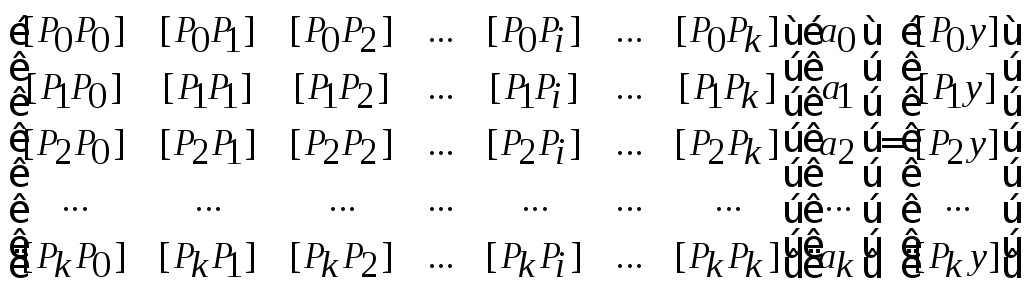, (7.24)

где [ ] - знак гауссовой суммы.

Эта система из k уравнений с k неизвестными имеет единственное решение. Решать такую систему при полиномах P_j общего вида затруднительно. Для упрощения, на полиномы P_j накладывают условия ортогональности:

. (7.25)

Согласно этим условиям все недиагональные элементы в (7.24) - коэффициенты , т.е. суммы произведений полиномов степеней i и j , равны нулю.

Матрица коэффициентов в (7.24) вырождается в диагональную. Система (7.24), следовательно, распадется на k независимых уравнений, каждое из которых позволяет определить один из искомых коэффициентов a_j или в общем виде:

a_j = /. (7.26).

Отсюда следует, что, определив единожды из условия (7.25) систему ортогональных полиномов, в последующем мы можем постоянно пользоваться ею, не прибегая к решению систем уравнений.

Существует несколько способов получения коэффициентов ортогональных полиномов Чебышева. Например, их можно получить на интервале значений x от --1 до +1 для полинома , задав условия:

.

Если шаг изменения x зафиксирован заранее, то его размер можно принять за единицу, привести некоторому интервалу, использовать целочисленные значения x, например, номера интервалов.

Рассмотрим получение коэффициентов ортогональных полиномов.