7.2.I.2. Геометрический смысл коэффициента корреляции

Пусть каждая из случайных величин X и Y подчиняется своему нормальному закону распределения. Положим, что X и Y суть две взаимно перпендикулярных координатных оси. Тогда совместное появление x и y в одном испытании мы можем рассматривать как точку на плоскости XY. Плотность вероятности в этой точке будет определяться двумерным нормальным распределением 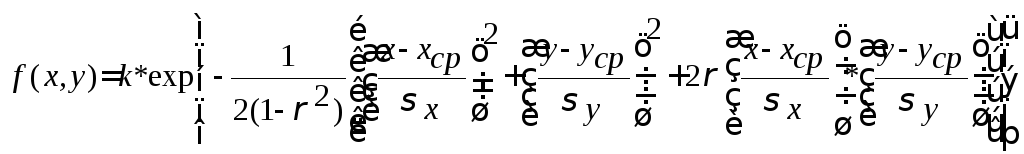,где - нормирующий коэффициент.

Функция плотности вероятности образует колоколообразную поверхность, показанную на рис. 7.2.

Выделим на плоскости прямоугольник со сторонами 2_x и 2_y соответственно, центр которого совпадает с центром распределения (x_cp y_cp) Пересечем теперь поверхность распределения плотности вероятности плоскостью, параллельной XY и отстоящей на расстоянии, соответствующем плотности распределения в точке x=_x. Сечение образует эллипс, называемый корреляционный эллипс. Этот эллипс вписывается в названный прямоугольник. Объем цилиндра до поверхности над этим эллипсом определяет вероятность попадания точки (x,y) в пределы, соответствующие стандарту. Вид эллипса зависит от соотношения стандартов _x и _y и значения коэффициента корреляции ρ. В частности при _x =_y и ρ=0 это будет круг, а при ρ= 1 - прямая линия.

Прямоугольник и эллипс

Рис. 7.2. Корреляционный эллипс (программно)

7.2.1.З. Назначение коэффициента корреляции

Коэффициент характеризует линейную статистическую связь.

При ρ =  1, как мы видим на рис. 7.3, ковариационный эллипс вырождается в прямую (колоколообразная поверхность ф.п.в. - в цилиндрическую).. Между _x и _y существует линейная зависимость: _y =A _x +B. Следовательно, распределение существует только для одной из этих СВ, а другая есть линейная функция первой.

------------------------------------------------------------------------------------------------

Здесь эллипсы и диагонали

------------------------------------------------------------------------------------------

Рис. 7.3. Форма корреляционного эллипса в зависимости от значения r

При r= 0 оси эллипса совпадают с осями распределения. Корреляционной связи нет. Однако может существовать нелинейная статистическая или даже функциональная связь. Например, функция y=cos x на интервале [-/2, /2] симметрична относительно оси y: каждому положительному значению x соответствует отрицательное. При вычислении оценки статистической связи между СВ x и y по (7.4) получим r=0 вместо функции cos и корреляции колебаний относительно этой кривой.

При 0< |r|< 1 существует линейная статистическая связь.

По значению модуля коэффициента корреляции тесноту связи оценивают как

очень слабую при 0. 00 0.2;

слабую при 0. 2 0.4;

среднюю при 0.4 0.7;

сильную при 0.7 0.9;

очень сильную при 0.9 0.9999.

Применение коэффициента корреляции

1. С его помощью оценивают статистическую связь пары случайных величин, независимость наблюдений величин, а также для сравнения силы связи разных пар величин.

2. Он служит для выявления функциональной линейной связи пары величин.

3.Коэффициент корреляции служит для характеристики совместных измерений пары величин.

4. Он необходим для оценки рассеивания (дисперсии S² или СКО) функции СВ. Например, найдем дисперсию суммы СВ X и Y

.

Из (7.3) следует, что

(7.5)

Учитывая (7.5), в итоге получаем

. (7.6)

Полученное выражение есть квадратичная форма, а матрицу R называют коррелляционной.