
ЛАБОРАТОРНАЯ РАБОТА 4. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ
ЗАДАНИЯ
-
Графическая иллюстрация численного интегрирования.
Выполнить m-файл
demosimp, который
демонстрирует интегрирование с помощью
квадратурной формулы Симпсона (формулы
парабол) для трех функций:
![]() ,
,
![]() ,
,
![]() .
Какова ошибка вычисления интеграла для
функции
.
Какова ошибка вычисления интеграла для
функции
![]() ?
?
Файл demotrap иллюстрирует применение квадратурной формулы трапеций для тех же функций и частичных отрезков.
Подобно
функции
![]() ,
,
![]() ,
,
![]() определенных в файлах xemx.m,
f8x3.m,
f16x4.m,
следует определять собственную функцию
определенных в файлах xemx.m,
f8x3.m,
f16x4.m,
следует определять собственную функцию
![]() по варианту задания.
по варианту задания.
-
Формула Симпсона.
Изучить функцию quadsimp, разобраться в том, как данная программа выполняет приближенное вычисление интеграла.
function [I,h] = quadsimp(func,a,b,N)
% Вычисление интеграла с помощью квадратурной формулы Симпсона.
% [I,h] = quadsimp(func,a,b,N)
% func - строковая переменная (имя функции), например, 'sin';
% [a,b] - отрезок интегрирования;
% N - число частичных отрезков, на которые разбивается [a,b];
% I - приближенное значение интеграла;
% h - половина длины частичного отрезка, равная (b-a)/2N.
h = (b-a)/(2*N);
sum1 = 0;
sum2 = 0;
for i=1:(N-1),
sum1 = sum1+feval(func,a+h*(2*i-1));
sum2 = sum2+feval(func,a+h*2*i);
end;
sum1 = sum1+feval(func,a+h*(2*N-1));
I = (feval(func,a)+feval(func,b)+4*sum1+2*sum2)*h/3;
С
помощью функции quadsimp
вычислить интеграл от
![]() на отрезке [a,b]
для некоторого числа частичных отрезков
N (например, для 5), а
также для числа 2N.
Сравнить полученные ошибки с теоретическими
оценками ошибок интегрирования. Для
многочленов какой степени формула
Симпсона является точной? Выписать в
тетрадь значения шага h,
полученной погрешности, теоретической
оценки.
на отрезке [a,b]
для некоторого числа частичных отрезков
N (например, для 5), а
также для числа 2N.
Сравнить полученные ошибки с теоретическими
оценками ошибок интегрирования. Для
многочленов какой степени формула
Симпсона является точной? Выписать в
тетрадь значения шага h,
полученной погрешности, теоретической
оценки.
Замечание: вычислять интеграл можно также с помощью функции plotsimp, которая имеет такие же входные параметры, что и quadsimp, но дополнительно строит график.
-
Формула прямоугольников и формула трапеций.
Создать в виде m-файлов две собственные функции численного интегрирования, одна из которых использует квадратурную формулу прямоугольников, а другая – формулу трапеций. Параметры вызова функций - такие же, как у quadsimp.
С помощью полученных m-файлов
вычислить определенный интеграл для
функции
![]() на отрезке [a,b]
с теми же значениями шага разбиения
отрезка интегрирования, что и в предыдущем
задании. Сравнить полученную погрешность
с теоретической оценкой. Выписать
значения шага, полученной погрешности,
теоретической оценки в тетрадь.
на отрезке [a,b]
с теми же значениями шага разбиения
отрезка интегрирования, что и в предыдущем
задании. Сравнить полученную погрешность
с теоретической оценкой. Выписать
значения шага, полученной погрешности,
теоретической оценки в тетрадь.
Для многочленов какой степени точна формула прямоугольников? Формула трапеций? Всегда ли формула парабол оказывается точнее формул прямоугольников и трапеций?
-
Вычисление интеграла с заданной точностью.
Вызвать демонстрацию примера
численного интегрирования с заданной
точностью (встроенная процедура
quaddemo). В примере
вычисление интеграла производится
встроенной функцией quad.
При помощи функции quad
вычислить определенный интеграл для
![]() на отрезке [a,b]
с различной точностью.
на отрезке [a,b]
с различной точностью.
ВАРИАНТЫ ЗАДАНИЙ
-
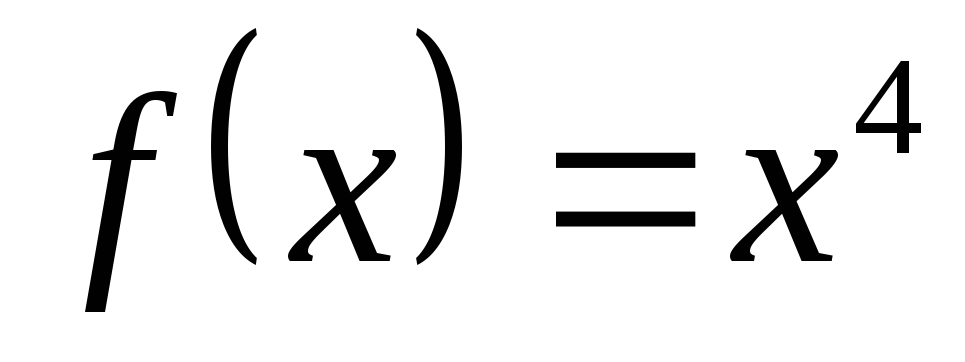 ,
a = 0, b = 1.
,
a = 0, b = 1. -
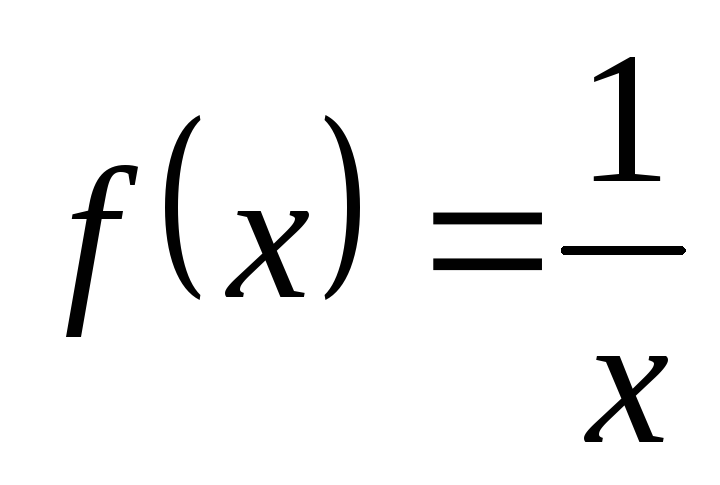 ,
a = 1, b = 2.
,
a = 1, b = 2. -
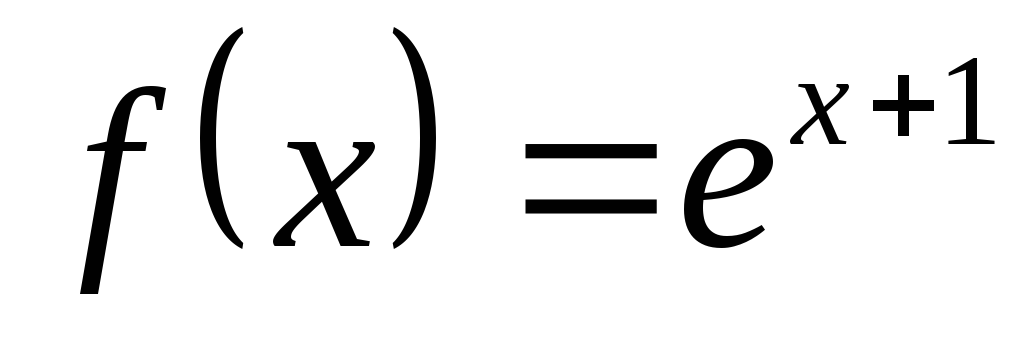 ,
a = -1, b =1.
,
a = -1, b =1. -
 ,
a = 0, b = .
,
a = 0, b = . -
 ,
a = 0, b = .
,
a = 0, b = .
ПРИЛОЖЕНИЕ. КВАДРАТУРНЫЕ ФОРМУЛЫ
Квадратурная формула
прямоугольников с остаточным членом
при условии
![]() :
:
![]() ,
где
,
где
![]() ,
,
![]() .
.
Квадратурная
формула трапеций с остаточным членом
при условии
![]() :
:
![]() ,
где
,
где
![]() ,
,
![]() .
.
Квадратурная
формула Симпсона с остаточным членом
при условии
![]() :
:
 ,
где
,
где
![]() ,
,
![]() .
.
Везде
в формулах
![]() .
.
