Лабы / Лабы 4 / Newton

Лабораторная работа №5.

Метод Ньютона.

Метод Ньютона – один из итерационных методов, отличающийся идейной простотой и быстрой сходимостью. Правило построения итерационной последовательности ( х_к ) получают из геометрических соображений , отсюда второе название этого метода – метод касательных.

Одномерный случай. Дано уравнение . Преобразуем его к виду и обозначим . Пусть найдена точка х_к - к-ое приближение к корню х^* , положим , тогда .

Таким образом, имеем : . Это и есть итерационная процедура Ньютона.

Геометрический смысл метода Ньютона: приближения к корню х^* осуществляется по абсциссам точек пересечения касательных к графику данной функции, проводимых в точках, соответствующим предыдущим приближениям.

Х_к

Х_к-1

Х_к+1

Х^*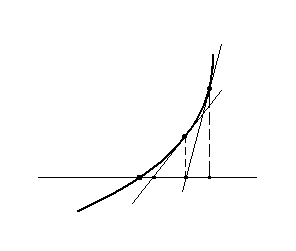

Многомерный случай. Пусть задана система уравнений:

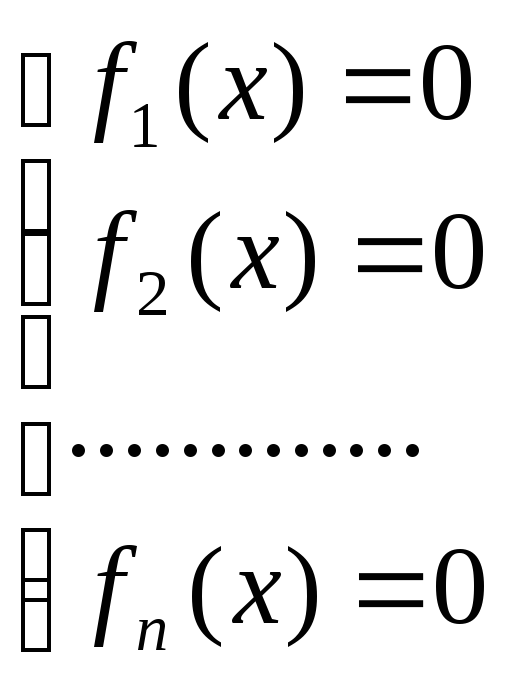где

Эта система эквивалентна уравнению , где - вектор-функция от векторного аргумента.

Аналог одномерного случая:

где 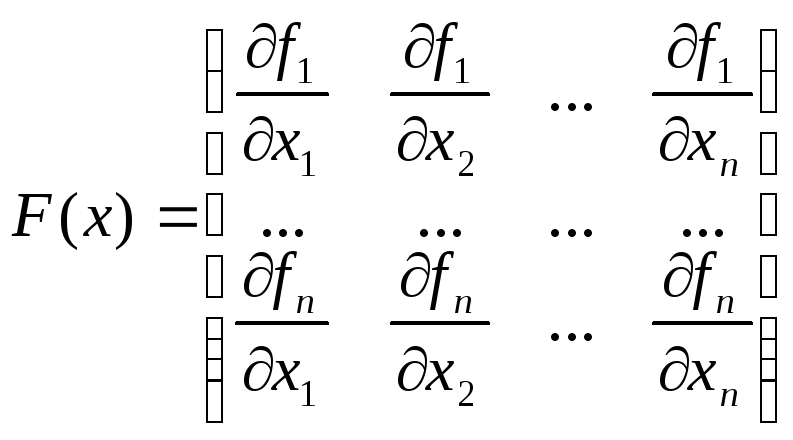- матрица Якоби .

Задание к лабораторной работе.

1.Разобраться в работе функции Nuton, которая вычисляет корни полинома с помощью одномерной итерационной процедуры Ньютона. В качестве параметров ей передаются коэффициенты многочлена, начальное приближение Х₀ и необходимая точность Ерs . Найти корни уравнения =0.

2.Разобраться в работе функции NutonM, реализующей многомерный случай использования метода Ньютона. Параметры функции :

PolynomHandle – строковая константа, соответствующая файлу-функции, содержащему описание вектор-функции ;

EcobyHandle – строковая константа, соответствующая файлу-функции, описывающему матрицу Якоби для данной системы ;

X0 – вектор начальных приближений ;

Eps – необходимая точность.

3. С помощью NutonM найти решения систем, создав соответствующие файлы, описывающие и матрицу Якоби:

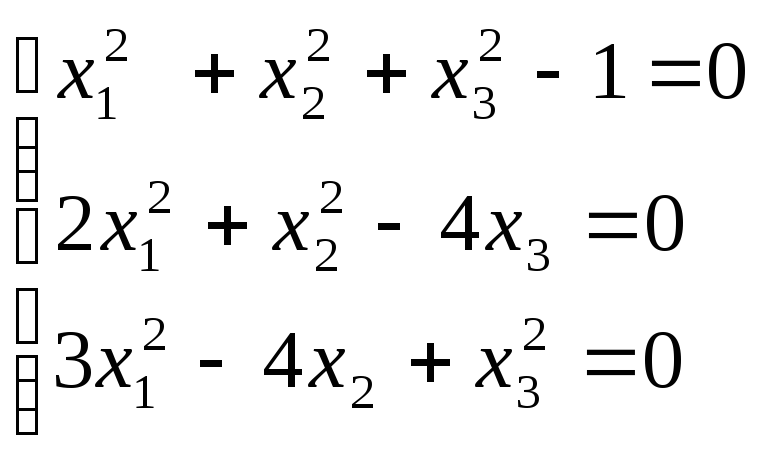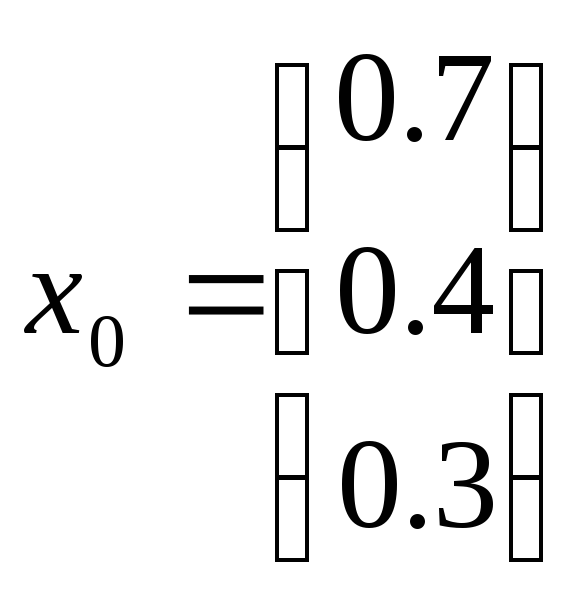
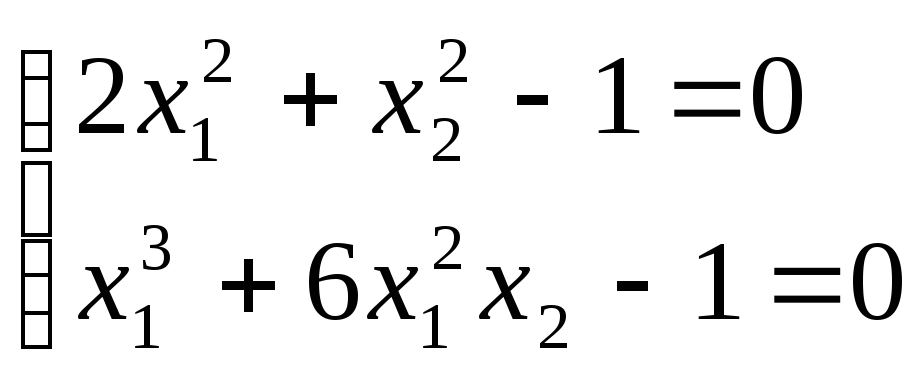в качестве начального приближения взять

в качестве начального приближения взять