Решение плохо обусловленных систем линейных уравнений.
-
Познакомиться с командами input, eye, diag, norm, det , cond, pinv, nnls, “ \ ”.
-
Создать собственный m-файл, реализующий следующую последовательность действий 2.1. По введенным с клавиатуры числам n и ep сформировать матрицу размерности n*n со следующей структурой:
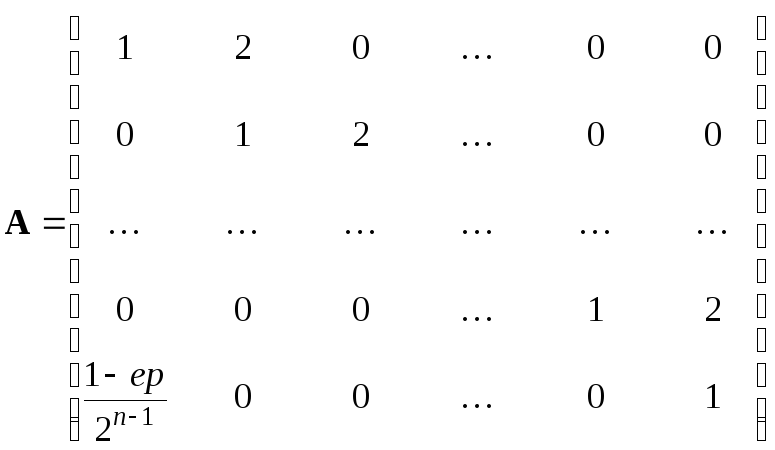и
вектор-столбец правой части
,
т.е.
.
Тем
самым будет задана система ЛАУ
.
(*)
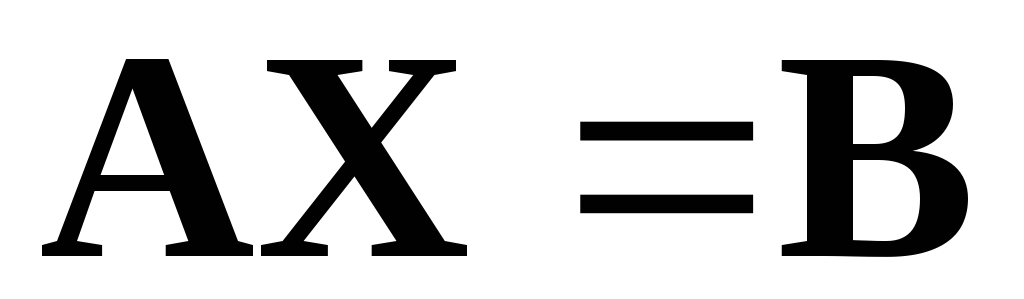2.2.
Вычислить
det(A),
cond(A),
(см.
help inv, help \ ), epsilon=
(см.
help norm).
Дальнейшие
действия выполняются с помощью
полученного m-файла. -
Убедиться, что при ep=1: detA=1 (для любого n), а точным решением системы (*) является вектор
. -
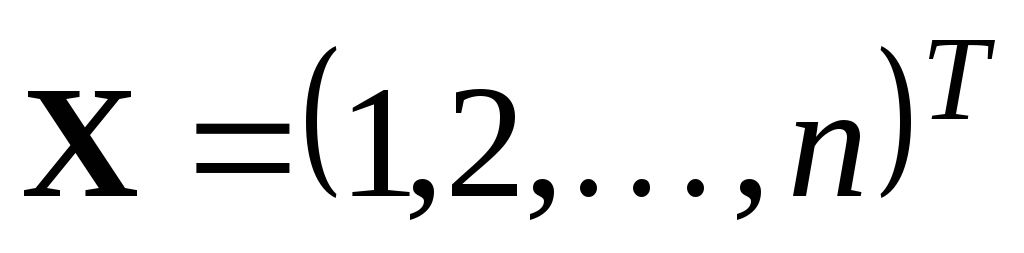Проверить, что при
:
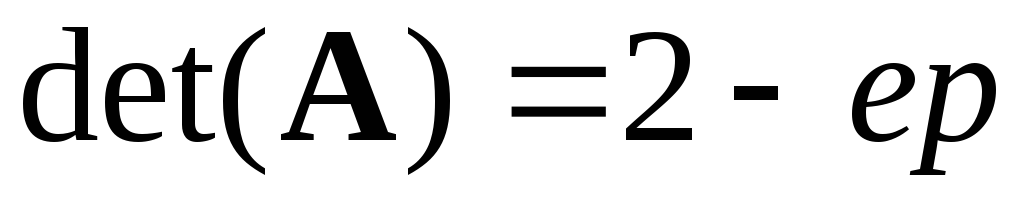(при нечетных n)
и
(при четных n). -
Последовательно уменьшая величину ep (например, делением пополам, начальное значение ep=1) для фиксированного значения n, например, n=20, вычислить det(A), cond(A),
,
epsilon=
.
Обратите внимание на то, что при малых
значениях ep
система становится «плохо обусловленной»,
о чем свидетельствует большое значение
числа обусловленности, определяемого
командой cond(A). -
Меняя произвольно пару параметров (ep,n), исследовать зависимость ошибки epsilon=
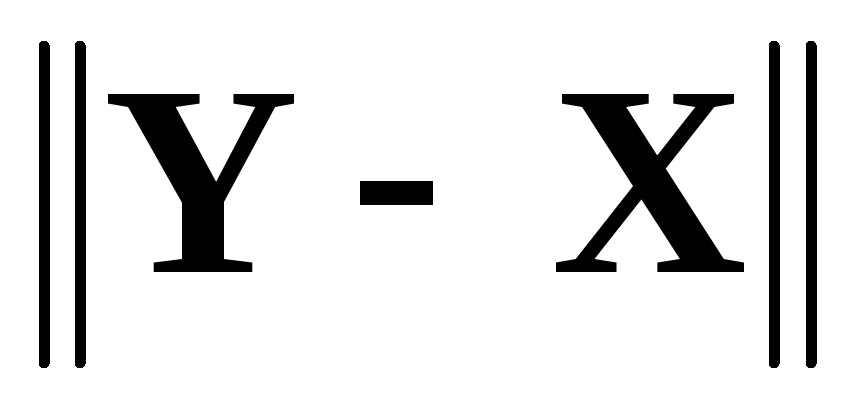от (ep,n).
Результаты свести в таблицу. -
При малых значениях ep и больших n (n=20..40) найти решение системы (*) в среднеквадратичной норме (help nnls), решение с помощью псевдоинверсии (help pinv). Сравнить с решением, полученным при помощи обычной инверсии (help inv).
-
Деформировать матрицу A, отбросив последнюю строку. При этом матрица становится прямоугольной, система – недоопределенной, а её решение в обычном смысле – не существует. Однако по-прежнему существует решение в среднеквадратичной норме, которое можно найти командой nnls или \. Найдите это решение.
-
Составить протокол, который должен содержать результаты выполнения пунктов 5-8, отчитаться преподавателю.