Московский институт электронной техники

Технический университет

Курсовая работа

Методы прикладной математики

Тема: Решение дифференциальных уравнений в частных производных разностными методами.

Выполнил: студент МП-32

Козлов Андрей

Руководитель: Кожухов И.Б.

Москва.1998.

Задание: Найти с помощью разностных методов решение дифференциального уравнения в частных производных

Уравнение относится к уравнениям зллиптического типа.

Исследование стационарных процессов различной физической природы часто приводит к необходимости решать уравнения эллиптического типа. Простейшим и наиболее распространенным уравнением эллиптического типа является уравнение Пуассона:

(1)

однородное уравнение Пуассона (при f(x,y)=0) называется уравнением Лапласа. Таким уравнением, например, описываются явления электростатики и магнитостатики. В частности, потенциал (x,y) электрического поля, образованного системой электродов и объемным зарядом частиц плотностью (x,y) удовлетворяет всюду, внутри области, не занятой электродами уравнению:

x,y (x,y)Г(G), (2)

где Г(G)- граница области G ;  (x,y) - функция , определенная для всех точек границы.

Уравнения (1),(2) называют первой краевой задачей для уравнения Пуассона .

Подобной же установке удовлетворяет задача стационарного двумерного распределения температуры в пластине конечной толщины, если внутри пластины распределены по заданному закону источники (стоки) тепла, описываемые функцией f(x,y) , a на границах поддерживается заданная температура.

Метод сеток состоит в сведении решения краевой задачи к решению системы алгеброических уравнений для так называемой сеточной функции. Для этого область G непрерывного изменения аргумента заменяется областью дискретного его изменения. Дифференциальный оператор заменяется некоторым разностным оператором. Краевые и начальные условия заменяются на соответствующие разностные аналоги. Выберем в области, где ищется решение дифференциального уравнения, некоторое конечное множество точек, в которых мы будем искать решение уравнения. Ясно, что чем больше мы возьмем таких точек, тем точнее решим уравнение. Множество таких точек называется сеткой, отдельные точки-узлами сетки. Функция, определенная в узлах сетки , называется сеточной функцией.

Пусть дан линейный дифференциальный оператор L , действующий на функцию x . Заменяя входящими в L  производные разностными отношениями, получим вместо L  разностное выражение L_h _h являющееся линейной комбинацией значений сеточной функции _h на некотором множестве узлов сетки, называемом сеточным шаблоном. Такая приближенная замена L на L_h _h называется аппроксимацией дифференциального оператора разностным оператором.

Говорят, что L_h апроксимирует дифференциальный оператор L с порядком аппроксимации m>0 в точке x, если

(x)=L_hv(x)-Lv(x)=o(h^m).

Будем решать задачу методом Зайделя, для этого существует определенный алгоритм, в подробности которого вдаваться не будем.

В алгоритме используется шаблон “крест”:

Апроксимация дифференциального оператора на этом шаблоне имеет вид:

, где h1 - шаг сетки по i и h2-шаг сетки по j.

Если известна искомая функция U(x,y) в точках :

(i-1,j) ; (i+1,j) ; (i,j+1) ; (i,j-1)

то значение U(x,y) в точке (i,j) может быть приближенно найдено следующим образом:

, где .

Это уравнение должно выполняться для всех внутренних узлов сетки, т.е. для .Для того, чтобы система стала полностью определенной надо дополнить ее уравнениями, полученными при апроксимации начальных и граничных условий. Для нашего случая зададим условия:

,

За 140 итераций с точностью 0.99 получим :

Г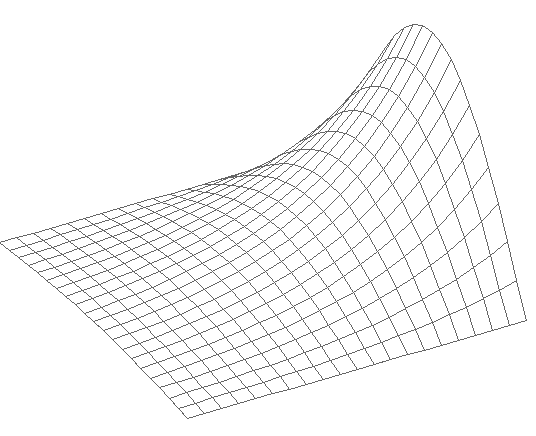 рафик функции нашей задачи решенной

по методу Зейделя имеет вид:

Представим графики сечений функции решения данной задачи:

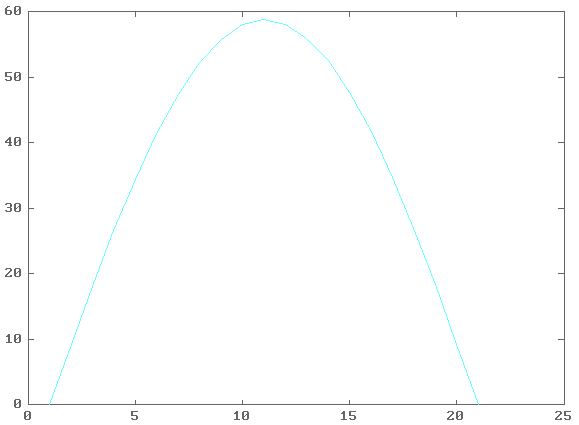
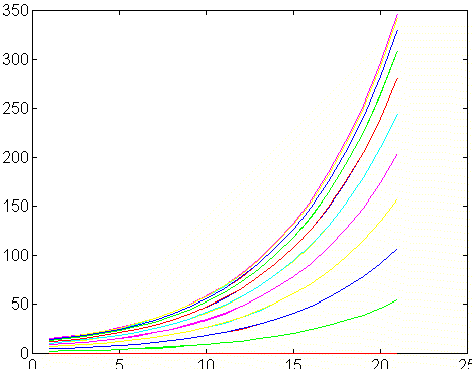
Таблица результатов:

Программа:

clc

clear

M=5

N=6

maxx=1000

EPS=0.01

mu=1

disp(‘Хотите что нибудь изменить? (y/n):');

key=input('','s');

if key=='y'|key=='Y',

M=input('Введите число столбцов:=');

if (M>90|M<2),

return

end

N=input('Введите число строк:=');

if (N>90|N<2),

return

end

maxx=input('Введите максимальное число итераций max:=')

EPS=input('Введите EPS:=')

mu=input('Введите (1<mu<2) mu:=')

end;

%------------------------------------------------------------

h1=1/M;

h2=1/N;

gamma=h2/h1;

u=ones(M+1,N+1);

error=ones(11,11);

for i=1:M+1;

u(i,1)=0;

u(i,N+1)=0;

end;

for j=1:N+1;

yj=(j-1)/N;

u(1,j)=15*sin(pi*yj);

u(M+1,j)=15*exp(pi)*sin(pi*yj);

end;

%----------------------------------------------------------------

A=1;

k=0;

while k<maxx

k=k+1;

clc;

disp('Итерация номер :');

disp(k);

disp('Текущая точность :');

disp(A);

disp('Заданная точность :');

disp(EPS);

A=0;

for i=2:M;

for j=2:N;

X=1/(2*(1+gamma^2))*(u(i,j-1)+u(i,j+1)+gamma^2*(u(i-1,j)+u(i+1,j)))-(h2*h2/(2*(1+gamma^2)))*30*(i/M*i/M+j/N*j/N-i/M-j/N);

X=mu*X+(1-mu)*u(i,j);

r=abs(X-u(i,j));

if r<=A;

u(i,j)=X;

else

A=r;

u(i,j)=X;

end;

end;

end;

if A<=EPS

disp('Точность');

disp(A);

disp('Параметр сходимости');

disp(mu);

disp('Число итераций');

disp(k);

disp('Матрица');

disp(u);

disp('Нажмите любую клавишу');

pause;

key=3;

while key~22,

clc;

ey=menu('Вид графика ','сечение по Х','сечение по Y','3D show','3d show 1','Контур','exit');

if key==1 ,

x=input('x=');

if (x>M|x<0),

return

end

plot(u(x,:));

pause;

end;

if key==2 ,

y=input('y=');

if (x>N|x<0),

return

end

plot(u(:,y));

pause;

end;

if key==3 ,

mesh(u);

pause;

for t=1:30:360

mesh(u,[t,0]);

pause;

end;

end;

if key==4 ,

mesh(u);

pause;

for t=1:30:360

mesh(u,[t,45]);

pause;

end;

end;

if key==5 ,

contour(u)

pause;

end;

if key==6 ,

return;

end

end;

end;

if k>maxx;

disp('Заданная точность еще не достигнута попробуйте с другими параметрами')

disp('Press any key....')

A

mu

k

pause;

return;

end;

end;

%---------------------------------------------------------------------

ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА

1. В.Г.Долголаптев, В.Н.Земсков. Численные методы решения разностных уравнений математической физики. Москва 1997

10