Московский Государственный Институт Электронной Техники

(Технический Университет)

кафедра Высшей Математики - I

Курсовая работа

по курсу

“Методы прикладной математики”

на тему

“Приближённое решение краевых задач математической физики методом сеток.”

Выполнил: Полушин Д.Б.

гр. МП - 32

Москва

1999 Г. Методические указания и постановка задачи.

1. Тема.

Приближенное решение краевой задачи математической физики методом сеток.

2. Цель работы.

Изучить основные понятия теории конечно-разностных методов решения краевых задач математической физики и уметь применять их на практике. Численное решение задачи осуществляется на персональном компьютере IBM PC/AT i486 в среде MATLAB. Преимущество использования этой cреды — богатый набор командных программ, реализующих большинство стандартных задач линейной алгебры и методов оптимизации, а также статистической обработки результатов. MATLAB обладает также хорошими графическими возможностями отображения результатов.

3. Порядок работы.

1. Познакомиться с основными понятиями метода сеток и методикой численного решения разностных уравнений, аппроксимирующих краевую задачу.

2. Классифицировать уравнение и проверить корректность постановки данной в варианте краевой задачи и соответствие её физическому смыслу.

3. Разобраться с методикой построения явных и неявных разностных схем конечно-разностных систем для данного типа уравнения.

4. Разобраться с устойчивыми методами решения явной и неявной схем.

5. Реализовать программу, осуществляющую решение в среде MATLAB.

6. Получить численные результаты для своего варианта. Оформить их в виде таблиц, построить необходимые кривые и поверхности уровней, иллюстрирующие решение задачи.

7. Оформить курсовую работу в соответствии с общим требованиями к курсовым работам. В теоретической части должны быть кратко освещены следующие вопросы:

• Классификация уравнения. Вскрыть физический смысл тех явлений, которые описываются данной математической постановкой задачи.

• Корректная постановка: граничные и начальные условия и их соответствие физическому смыслу.

• Понятия: сеточный шаблон, порядок аппроксимации разностных схем, сходимость, устойчивость решения.

• Выбор шагов сетки и оценка погрешности метода.

Выполнение работы.

1. Классификация краевой задачи и её физический смысл

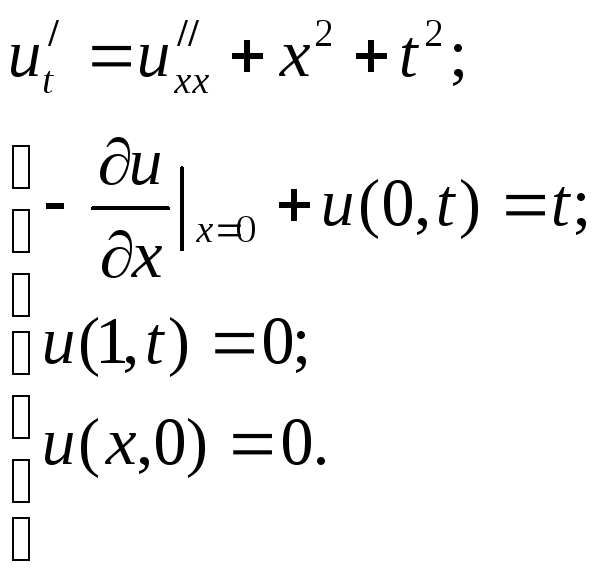
Данное уравнение является уравнением параболического типа и физически отражает процесс распределения тепла в однородном стержне длиной единица. Его решением является функция - значение температуры стержня в точке в момент времени, где , .

- начальное условие, означающее, что в начальный момент времени температура стержня была равна нулю.

- граничное условие первого рода, означающее, что температура на правом конце стержня поддерживается постоянной и равной нулю.

(или )- граничное условие третьего рода, означающее, что на левом конце стержня по закону Ньютона происходит теплообмен с окружающей средой, температура , которой известна.

Коэффициент теплопроводности стержня равен 1.

- плотность источников тепла.

2. Решение сеточного уравнения.

2.1. Явная разностная схема.

В явной разностной схеме значение сеточной функции на последующем слое полностью определяется значением её на предыдущем слое по рекурентным формулам. В данной задаче апроксимацию дифференциальных операторов проведём по следующему шаблону :

Тогда конечно-разностная система уравнений имеет вид :

Значение температуры на слое явно выражается через значение температуры на слое по формуле :

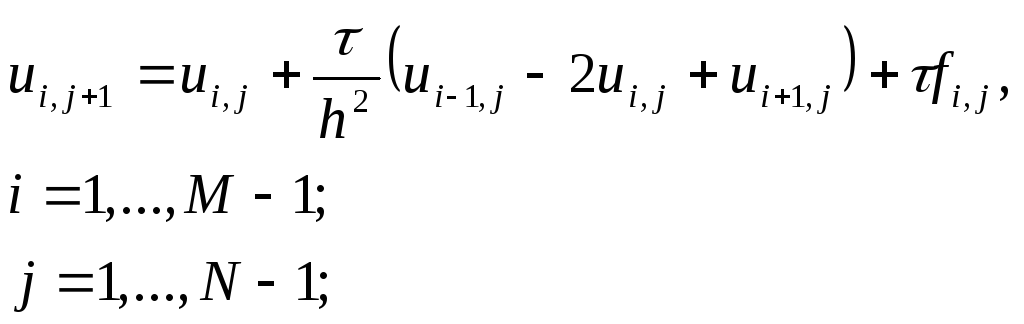
Порядок аппроксимации данной разностной схемы равен . Необходимо получить ,

где

Найдем по методу “фиктивного узла”:

Из граничного условия третего рода выразим :

В итге получаем:

Практическая реализация данного метода возможна лишь при таких соотношениях между шагами сетки ипри которых выполняется условие устойчивости решения к ошибкам округления и неточностям в начальных данных. Это условие имеет вид .

Текст функции, вычисляющий матрицу решения размерностьюприведён ниже.

clear;

N=20000;

M=100;

h=1/M;

t=1/N;

U=zeros(M+1,N+1);

f=zeros(M+1,N+1);

for i=1:M+1

for j=1:N+1

f(i,j)=(h*(i-1))^2+(t*(j-1))^2;

end;

end;

for j=1:N

U(1,j+1)=2*t/(h*h)*U(2,j)+U(1,j)*(1-2*t*(1+h)/(h*h))+2*t*t*j/h+(t^3)*j*j;

for i=2:M

U(i,j+1)=U(i,j)+t/(h*h)*(U(i-1,j)-2*U(i,j)+U(i+1,j))+t*f(i,j);

end;

% U(1,j+1)=U(1,j)+(2*t)/(h*h)*(U(2,j)-U(1,j)+h*(t*j-U(1,j)));

% U(1,j+1)=((h*h)/(2*t)*U(1,j)+U(2,j+1)+h*h/2*f(1,j+1)+h*t*j)/(1+h*h/(2*t)+h);

end;

y=zeros(M+1,10);

for i=1:M+1

for j=1:10

y(i,j)=U(i,j*20);

end;

end;

i=1:1:M+1;

plot(i,y);

pause;

mesh(U);

pause;

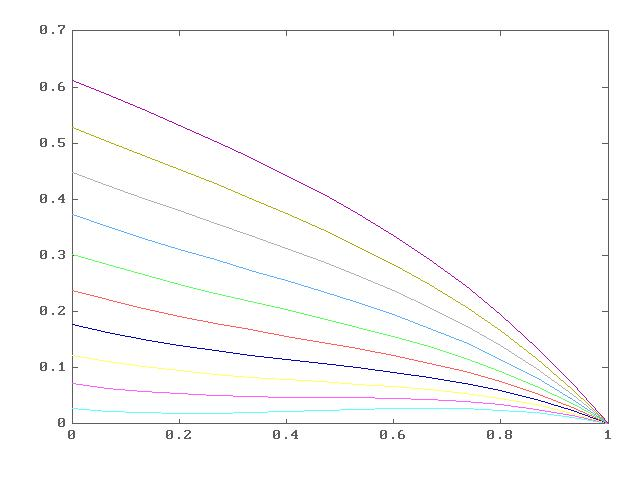
Решение полученное при явной схеме.

sColumns 1 through 7

0.0260 0.0706 0.1211 0.1764 0.2365 0.3015 0.3715

0.0205 0.0598 0.1054 0.1561 0.2121 0.2733 0.3398

0.0184 0.0529 0.0935 0.1395 0.1909 0.2478 0.3101

0.0188 0.0490 0.0848 0.1259 0.1724 0.2243 0.2818

0.0209 0.0471 0.0781 0.1141 0.1554 0.2019 0.2537

0.0238 0.0462 0.0723 0.1031 0.1387 0.1792 0.2246

0.0262 0.0447 0.0660 0.0914 0.1210 0.1549 0.1931

0.0269 0.0413 0.0576 0.0772 0.1003 0.1270 0.1571

0.0240 0.0340 0.0452 0.0588 0.0748 0.0935 0.1146

0.0158 0.0210 0.0268 0.0338 0.0422 0.0520 0.0632

0 0 0 0 0 0 0

Columns 8 through 10

0.4464 0.5262 0.6110

0.4117 0.4889 0.5715

0.3780 0.4515 0.5305

0.3447 0.4133 0.4874

0.3108 0.3734 0.4412

0.2750 0.3303 0.3906

0.2356 0.2826 0.3339

0.1909 0.2282 0.2691

0.1384 0.1648 0.1937

0.0757 0.0897 0.1050

0 0 0

s