Московский Государственный Институт Электронной Техники

(Технический Университет)

кафедра Высшей математики

КУРСОВАЯ РАБОТА

по

“Методам прикладной математики”

на тему

“Приближенное решение краевых задач математической физики методом сеток.”

Выполнил: ТугбаевМ.Г. гр. МП-31 Руководитель: Хахалин С.Я.

Москва 1998 г.

Содержание:

1. Классифиация краевой задачи и ее физический смысл;

2. Явная разностная схема;

3. Неявная разностная схема;

4. Анализ полученных данных;

5. Графики решений;

6. Таблицы результатов и тексты программ;

7. Используемая литература.

1. Классифиация краевой задачи и ее физический смысл.

Это линейное дифференциальное уравнение второго порядка параболического типа. Оно описывает распределение тепла в однородном стержне длины 1 в зависимости от времени. Перепишем его в другом виде:

(1)

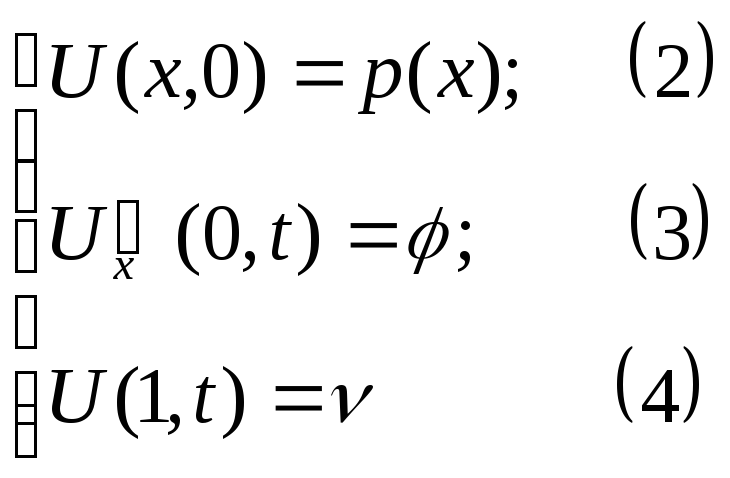
. Начальное условие задает распределение температуры на всем стержне в начальный момент времени t = 0. Граничное условие второго рода обозначает то, что на левом конце стержня по закону Ньютона происходит теплообмен с окружающей средой, а граничное условие первого рода ,что температура на правом конце стержня не зависит от времени

2. Явная разностная схема.

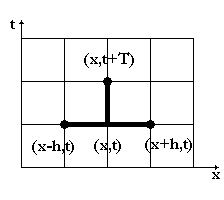
В расчетах будем использовать сетку с (M+1)

узлом по оси X и (N+1) по оси T. Тогда:

Явная конечно-разностная схема получается,

если использовать шаблон на рисунке 1. Конечно-

разностная система система будет выглядеть следую-

щ

Рисунок 1.

им образом:

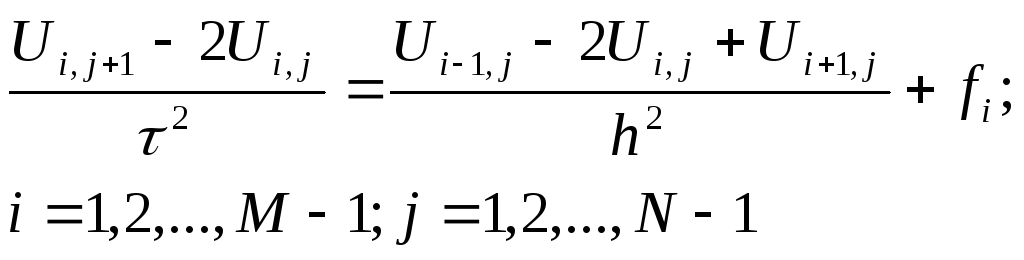(5)

с погрешностью аппроксимации .

Чтобы аппроксимировать краевое условие второго рода (3) разложим в ряд Тейлора функцию в окрестности точки:

.

Подставим в это уравнение из уравнения теплопроводности (1) :

и выразим производную при:

.

Затем заменяем левой разностной производной

получим:

(6)

Записывая краевое условие второго рода в узле :

и подставляя сюда производную из (6) получим :

.

с погрешностью аппроксимации .

Выражаем из этого уравнения :

. (7)

Из (3),(4) получаем соответственно:

(8)

Записываем систему из (5),(7),(8) в удобном для вычислений виде :

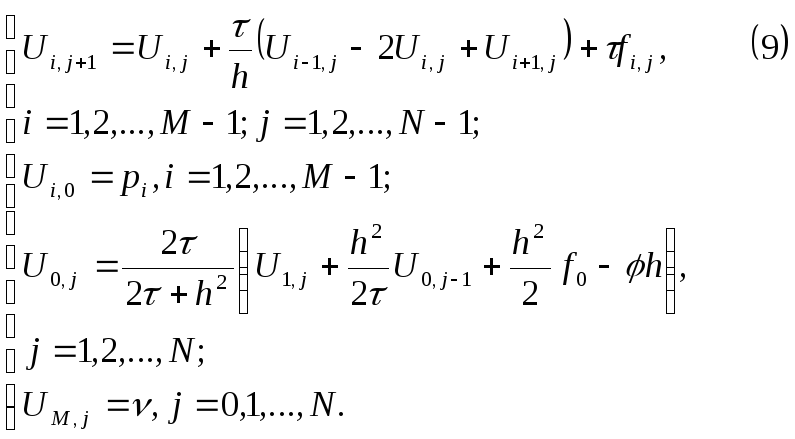
Погрешность аппроксимации данной схемы равна .

Равенство (9) представляет из себя рекурентну формулу для вычисления

решений системы. Так как при таком вычислении накапливается ошибка, то для устойчивости этой схемы на и должны накладываться ограничение: (следует из ).

3. Неявная разностная схема.

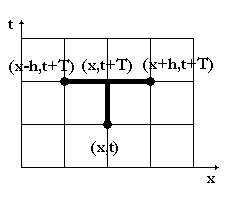
Неявная конечно-разностная схема получается,

если использовать шаблон на рисунке 2. Конечно-

разностная система система будет выглядеть следую-

щим образом:

Рисунок 2.

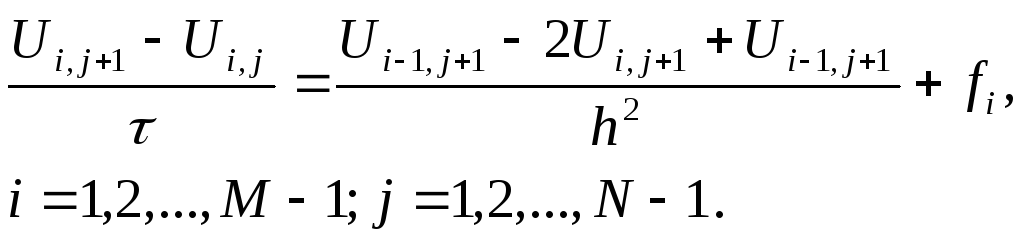
Запишем это равенство в следующем виде:

(10)

Граничное условие второго рода аппроксимируется также как и в первом случае:

.

с погрешностью .

Запишем это равенство в виде:

(11)

Из (3),(4) получаем соответственно:

(12)

Получим из (10),(11),(12) систему:

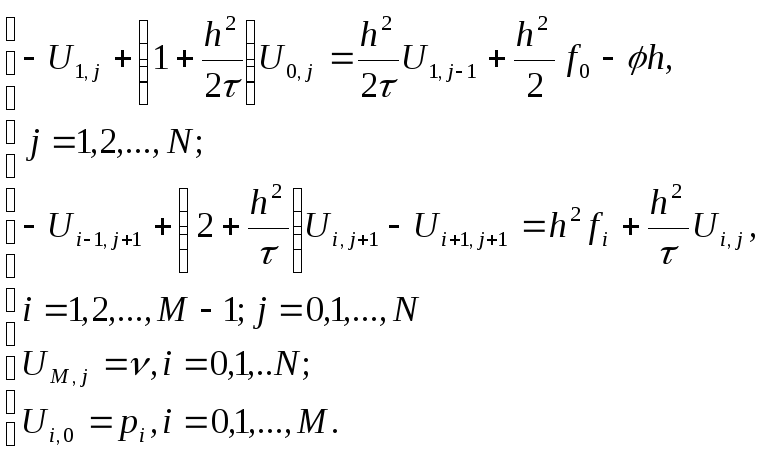(13)

с погрешностью аппроксимации .

Для вычисления решения по неявной разностной схеме на компьютере используют метод прогонки. Коэффициенты, для которого определяються из системы (13).

Формулы :

определяют прямой ход прогонки, а формулы:

обратный.

Так как :

, ,,,;

, ;

,,

то имеют место неравенства:

,,,

гарантирующие корректность и устойчивость метода прогонки.