Московский институт электронной техники (Технический университет)

Кафедра Высшей математики - I

Курсовая работа

по курсу «Численные методы»

Вариант 5.

Выполнил: Ванюков В.М.

Группа: МП-32

Руководитель: Немировская О.Э.

Москва 2002 г.

Постановка задачи

Задание: получить приблизительное решение данной краевой задачи уравнения в частных производных математической физики методом сеток.

(1)

0< x,y<1 (2).

Данное уравнение является уравнением гиперболического типа и физически отражает процесс колебания струны. Искомое решение U=U(x,y) - вертикальное отклонение струны в точке х в момент времени y.

Данная краевая задача состоит в нахождении функции U=U(x,y), удовлетворяющей уравнению (1), а также заданным начальным и граничным условиям (2).

Граничное условие первого рода U=U(1,y) определяет закон движения правого конца струны. Для левого конца в качестве граничного условия задано так называемое условие «упругого конца» (граничное условие третьего рода):

U_x (0,y)=U(0,y) .

Начальные условия U(x,0)=0 и U_y(x,0)=1 задают начальную форму струны и распределение скоростей в начальный момент времени.

Функция f(x,y) имеет смысл плотности внешней силы, рассчитанной на единицу длины.

РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ НЕЯВНОЙ РАЗНОСТНОЙ СХЕМЫ

Рассмотрим снова нашу краевую задачу . Для аппроксимации уравнения используем Т-образный пятиточечный шаблон . Уравнение аппроксимируется следующими уравнениями :

1. Аппроксимация дифференциального уравнения

Обозначим g=/h и запишем (1) к виду удобному для применения метода прогонки:

2. Аппроксимация 1-го начального условия

(3)

3. Аппроксимация 2-го начального условия

Для более точного аппроксимирования 2-го начального условия разложим u(x,y ) в окрестности точки (x,0) по формуле Тейлора

=1

и используя 1-ое и 2-ое начальное условия перейдем к конечным разностям:

Запишем (4) к виду удобному для применения метода прогонки:

4. Аппроксимация 2-го граничного условия

5. Аппроксимация 1-го граничного условия

в узле(0,1):

(5) при i=0 будет:

исключая фиктивный узел, получим:

(7)

при j2, в узле (0,j):

из (2):, тогда:

(8)

6. Вычисления прогоночных коэффициентов

Сначала найдем u(i,j) на слое j=1. Определим прогоночные коэффициенты.

Обозначим , тогда, используя (7),(5) и (6) получим систему:

получим прогоночные коэффициенты:

Теперь вычислим граничные прогоночные коэффициенты:

Методом прогонки находим u(i,1) где i=1...m ;

Теперь зная значения j=0,1 находим u(i,j ) где j=2...n.

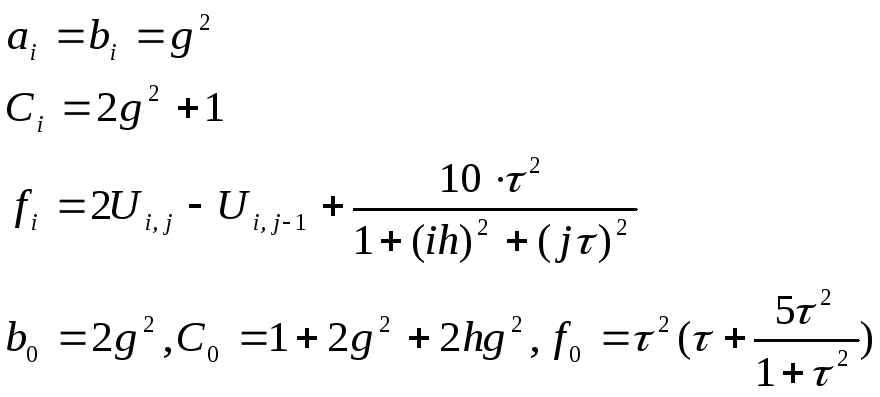
Текст программы в среде Matlab приведен в приложении.

РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ ЯВНОЙ РАЗНОСТНОЙ СХЕМЫ

В явной разностной схеме значение сеточной функции на последующем слое полностью определяется значением её на предыдущем слое по рекуррентным формулам. В данной задаче аппроксимацию дифференциальных операторов проведём по следующим шаблонам:

2.1 Аппроксимация дифференциального уравнения

Для сведения задачи к явной разностной схеме используем шаблон " крест".

Получаем конечно-разностную систему:

(3^*)

Обозначим g=/h и выразим через остальные значения сеточной функции, входящие в уравнение:

(3)

Уравнение (3) должно выполняться для всех внутренних узлов сетки. Для того чтобы система стала полностью определенной, необходимо дополнить ее уравнениями получаемыми из аппроксимации краевых и начальных условий.

2.2 Аппроксимация 1-го начального условия.

(4)

2.3 Аппроксимация 2-го начального условия.

Второе начальное условие в общем виде выглядит следующим образом: (конкретно в нашей задаче ). Для более точного его аппроксимирования разложим U(x,y) в окрестности точки (x,0) по формуле Тейлора:

Используя исходное уравнение и начальное условие получим:

Перейдем к конечным разностям, записываемым в узле (i,1), т.е. на первом слое:

(5^*)

Подставляя в эту формулу данные нашей конкретной задачи получаем:

(5)

Принимая во внимание уравнение (4) получаем:

(6)

Формула (6) используется на начальном этапе для вычисления значения функции U на первом слое по известным значениям функции U на нулевом слое и на границе. После того как значения U_i,j для j = 0 и j =1 определены, включается рекуррентная процедура, описываемая уравнением (3), и вычисляется U_i,j для всех i=1,2,..,M-1 для каждого фиксированного j = 2,..,N-1.

4. Аппроксимация 1-го граничного условия.

(7)