Московский Государственный Институт Электронной Техники

(Технический Университет)

кафедра Высшей Математики - I

Курсовая работа

по курсу

“Методы прикладной математики”

на тему

“Приближенное решение краевых задач математической физики методом сеток.”

Выполнил: Хмеленко А.

гр. МП - 32 Руководитель: Немировская О.Э.

Москва 2002 г.

Методические указания и постановка задачи.

1. Тема.

Приближенное решение краевой задачи математической физики методом сеток.

2. Цель работы.

Изучить основные понятия теории конечно-разностных методов решения краевых задач математической физики и уметь применять их на практике. Численное решение задачи осуществляется на персональном компьютере в среде MATLAB. Преимущество использования этой среды — богатый набор командных программ, реализующих большинство стандартных задач линейной алгебры и методов оптимизации, а также статистической обработки результатов. MATLAB обладает также хорошими графическими возможностями отображения результатов.

3. Порядок работы.

1. Познакомиться с основными понятиями метода сеток и методикой численного решения разностных уравнений, аппроксимирующих краевую задачу.

2. Классифицировать уравнение и проверить корректность постановки данной в варианте краевой задачи и соответствие её физическому смыслу.

3. Разобраться с методикой построения явных и неявных разностных схем конечно-разностных систем для данного типа уравнения.

4. Разобраться с устойчивыми методами решения явной и неявной схем.

5. Реализовать программу, осуществляющую решение в среде MATLAB.

6. Получить численные результаты для своего варианта. Оформить их в виде таблиц, построить необходимые кривые и поверхности уровней, иллюстрирующие решение задачи.

7. Оформить курсовую работу в соответствии с общим требованиями к курсовым работам. В теоретической части должны быть кратко освещены следующие вопросы:

• Классификация уравнения. Вскрыть физический смысл тех явлений, которые описываются данной математической постановкой задачи.

• Корректная постановка: граничные и начальные условия и их соответствие физическому смыслу.

• Понятия: сеточный шаблон, порядок аппроксимации разностных схем, сходимость, устойчивость решения.

• Выбор шагов сетки.

Выполнение работы.

1. Классификация краевой задачи и её физический смысл

Классификация задачи.

Линейное дифференциальное уравнение второго порядка такого вида относится к уравнениям эллиптического типа. Данное уравнение называется также уравнением Лапласа. Оно описывает стационарное распределение температур (не зависящее от t) тонкой изотропной пластинки изолированной от внешней среды.

Подобной постановке удовлетворяет задача стационарного двумерного распределения температуры в пластине конечной толщины, если внутри пластины распределены по заданному закону источники тепла, описываемые функцией f(x, y) ,а на границах пластины поддерживается заданная температура. Именно такая задача имеет место в данном конкретном случае.

Имеем квадратную пластину единичной ширины. Начальные условия задают распределения температуры на четырех сторонах границы квадрата, а функция f(x, y) определяет расположение источников теплоты на поверхности пластины.

Пусть дан линейный дифференциальный оператор L , действующий на функцию . Заменяя входящие в производные разностными отношениями, получим вместо разностное выражение , являющееся линейными комбинациями значений сеточной функции на множестве узлов сетки, называемом шаблоном. Такая приближенная замена на называется аппроксимацией дифференциального оператора разностным оператором или разностной аппроксимацией оператора L . Прежде чем приступить к разностной аппроксимации оператора необходимо выбрать шаблон, т. е. указать множество соседних с узлом узлов, в которых значения сеточной функции могут быть использованы для аппроксимации оператора L .

Для аппроксимации дифференциального уравнения используем шаблон “крест”, показанный на рис.1.

j+1 i i+1

j

j-1

Рис.(1)

Введем сетку

(1)

содержащую M+1 узлов по оси x и N+1 узлов по оси y, причем - множество внутренних узлов сетки.

Пусть есть оператор дифференцирования: = (2) аппроксимируем его в каждом внутреннем узле сетки центральными разностями второго порядка.

(3)

Обозначим .

Применяя к нашей задаче, получим:

(4)

i=1,2,...,M-1; j=1,2,...,N-1.

Система аппроксимирует уравнение Лапласа на сетке с порядком точности и соответствует пятиточечному шаблону “крест”.

Составленная программа реализует нахождение приближенного решения поставленной задачи методом верхней релаксации.

Текст программы:

M=10;

N=10;

h1=4/M;

h2=2/N;

mu=1.7;

maxx=25;

gamma=h2/h1;

u=ones(N+1,M+1);

for i=1:M+1;

u(1,i)=10*sin(pi*(i-1)*h1/8);

u(N+1,i)=0;

end;

for j=1:N+1;

u(j,1)=0;

u(j,M+1)=0;

end;

A=1;

k=0;

while k<maxx

k=k+1;

A=0;

for i=2:M;

for j=2:N;

X=1/(2*(1+gamma^2))*(u(j-1,i)+u(j+1,i)+gamma^2*(u(j,i-1)+u(j,i+1)));

X=mu*X+(1-mu)*u(j,i);

r=abs(X-u(j,i));

if r<=A;

u(j,i)=X;

else

A=r;

u(j,i)=X;

end;

end;

end;

end;

A

mesh(u);

Gr=zeros(11,11);

for i=1:11

for j=1:11

Gr(j,i)=u(j,i);

end

end

Y2=zeros(11,1);

Y4=zeros(11,1);

Y6=zeros(11,1);

Y8=zeros(11,1);

Y0=zeros(11,1);

Y10=zeros(11,1);

W=zeros(11,1);

for i=1:11

Y0(i)=Gr(1,i);

Y2(i)=Gr(3,i);

Y4(i)=Gr(5,i);

Y6(i)=Gr(7,i);

Y8(i)=Gr(9,i);

Y10(i)=Gr(11,i);

W(i)=(i-1)*2/5;

end

plot(W,Y0,'b',W,Y2,'k',W,Y4,'r',W,Y6,'g',W,Y8,'y',W,Y10,'m');

Для проверки сходимости решения при увеличении числа узлов сетки матриц, вычислим нормы разности матриц с различным числом узлов, в виде максимального отклонения значений в совпадающих узлах.

Размерность	U1=10x10 U2=20x20	U2=20x20 U3=40x40	U3=40x40 U4=80x80
Норма	0.0394	0.0232	0.0138

Как видно из таблицы, с увеличением числа узлов матрицы решения, норма уменьшается и следовательно решение сходится и является устойчивым.

График решения уравнения эллиптического вида схеме:

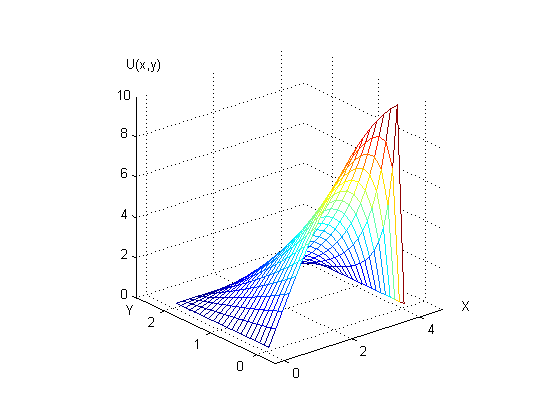
Элементы матрицы U1(i,j):

0 1.5643 3.0902 4.5399 5.8779 7.0711 8.0902 8.9101 9.5106 9.8769 0

0 1.3767 2.7167 3.9841 5.1440 6.1557 6.9698 7.5103 7.5907 6.4947 0

0 1.1975 2.3605 3.4562 4.4483 5.2890 5.9177 6.2255 5.9649 4.4622 0

0 1.0263 2.0220 2.9560 3.7892 4.4753 4.9462 5.0829 4.6496 3.1696 0

0 0.8633 1.7010 2.4800 3.1673 3.7157 4.0583 4.0829 3.5961 2.2994 0

0 0.7091 1.3936 2.0277 2.5800 3.0079 3.2500 3.2107 2.7451 1.6799 0

0 0.5595 1.0987 1.5957 2.0238 2.3464 2.5121 2.4453 2.0440 1.2141 0

0 0.4147 0.8142 1.1808 1.4937 1.7241 1.8324 1.7634 1.4501 0.8444 0

0 0.2743 0.5381 0.7795 0.9841 1.1321 1.1968 1.1426 0.9292 0.5343 0

0 0.1365 0.2676 0.3874 0.4885 0.5607 0.5910 0.5615 0.4538 0.2591 0

0 0 0 0 0 0 0 0 0 0 0

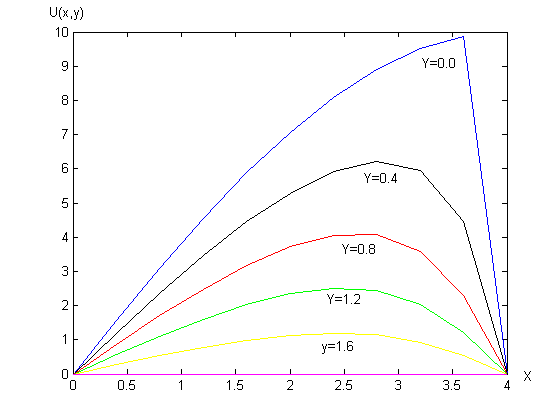
Срезы решения:

ИСПОЛЬЗУЕМАЯ ЛИТЕРАТУРА

1. Долголаптев В.Г., Земсков В.Н. Численные методы решения разностных уравнений математической физики. Методические указания к курсовой работе по высшей математике. /Под ред. А.В. Ефимова. – М.: Изд. МИЭТа, 1987. – 66 с.

2. Земсков В.Н., Хахалин С.Я. Метод сеток. Методические указания к выполнению курсовой работы на персональном компьютере. – М.: МИЭТ, 1998. – 64 с.: ил.

2