Московский Государственный Институт Электронной Техники

( Технический Университет )

Курсовая работа по теме :

Численные методы решения разностных уравнений математической физики

Вариант №11.

Выполнил: Ивченко В.Н.

Группа: МП-34

Руководитель: Соколова Т.В.

МОСКВА 2000 г.

Постановка задачи.

Задание: получить приблизительное решение данной краевой задачи уравнения в частных производных математической

физики методом сеток.

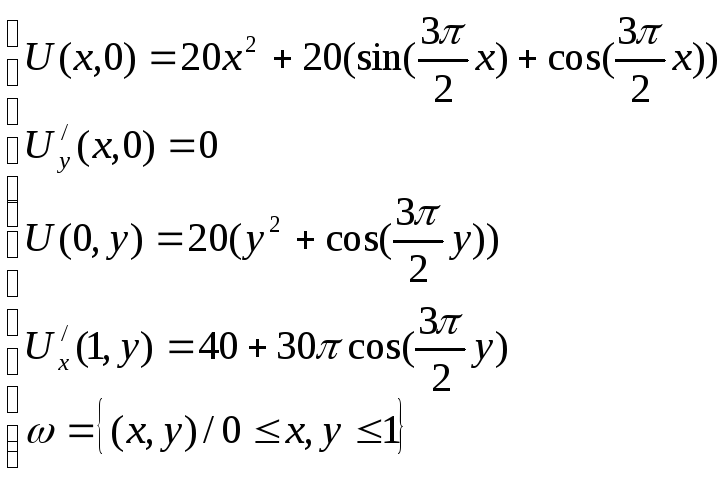
Данное уравнение является уравнением гиперболического типа и физически отражает процесс колебания струны. Искомое решение U(x,y) - вертикальное отклонение струны в точке x в момент времени t.

Данная краевая задача состоит в нахождении функции U(x,y), удовлетворяющей уравнению, а также заданным начальным и граничным условиям.

Граничное условие рода определяет закон движения правого конца струны так называемое условие «упругого закрепления».Для левого конца в качестве граничного условия задано условие

Начальные условия и задают начальную форму струны и распределение скоростей в начальный момент времени.

РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ ЯВНОЙ РАЗНОСТНОЙ СХЕМЫ

В явной разностной схеме значение сеточной функции на последующем слое полностью определяется значением её на предыдущем слое по рекуррентным формулам. В данной задаче аппроксимацию дифференциальных операторов проведём по следующим шаблонам

2.1 Аппроксимация дифференциального уравнения

Для сведения задачи к явной разностной схеме используем шаблон " крест".

Получаем конечно-разностную систему :

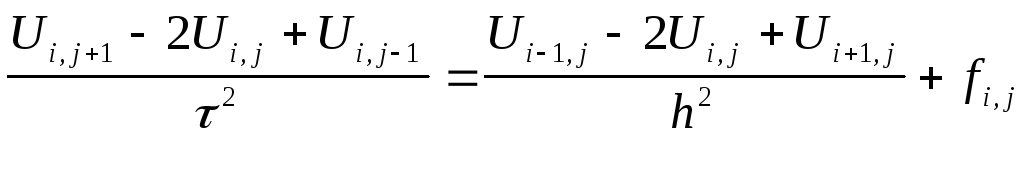
Обозначим и выразим через остальные значения сеточной функции,

входящие в уравнение:

i = 1,.....,m-1;

j = 1,.....,n-1.

Уравнение (1) должно выполняться для всех внутренних узлов сетки . Для того чтобы система стала полностью определенной , необходимо дополнить ее уравнениями получаемыми из аппроксимации краевых и начальных условий.

2.2 Аппроксимация 1-го начального условия.

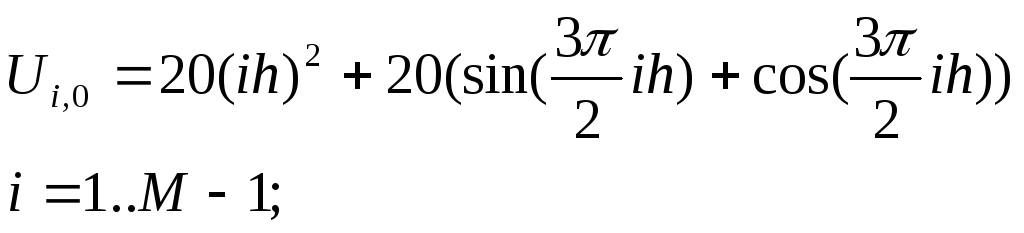(2)

2.3 Аппроксимация 1-го граничного условия.

Аппроксимация краевого условия второго рода используется только для нахождения решения на границе i=0 в явном виде:

(3)

2.4 Аппроксимация 2-го начального условия.

Для более точного аппроксимирования 2-го начального условия разложим в окрестности точки по формуле Тейлора и используя начальные условия перейдем к конечным разностям:

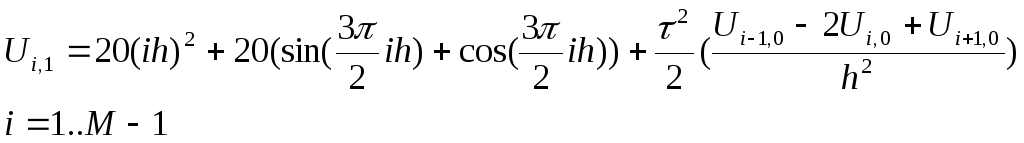(4)

Формула (4) используется на начальном этапе для вычисления значения функции U на первом слое, по известным значениям функции на нулевом слое и на границе .

5. Аппроксимация 2-го граничного условия.

Для более точного аппроксимирования 2-го граничного условия разложим в окрестности точки (1,y ) по формуле Тейлора:

Используя уравнение краевой задачи и второе граничное условие получаем:

Перейдя к конечным разностям, записываемыми в узле , получаем:

(5)

Выражая из него получаем:

(6)

Найдем необходимую точку. Из (4) , при

Откуда -

(7)

Из (5) , при :

Откуда -

(8)

Из (1) , при

(9)

Итак при и определены. Включается рекуррентная процедура.

Порядок аппроксимации данной разностной схемы .

Устойчивость решения.

Для уравнений гиперболического типа метод спектральных гармоник

приводит к следующему условию устойчивости:

(7),

т.е. если это условие устойчивости не будет выполнено, то в процессе рекуррентного решения возможно накапливание ошибок от слоя к слою.

Отсюда, в частности, получаем для явной схемы () условие устойчивости Куранта-Леви: .

РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ НЕЯВНОЙ РАЗНОСТНОЙ СХЕМЫ.

Рассмотрим снова краевую задачу . Для аппроксимации уравнения используем Т-образный пятиточечный шаблон . Уравнение аппроксимируется следующими уравнениями :

3.1 Аппроксимация дифференциального уравнения

Обозначим и запишем (1) к виду удобному для применения метода прогонки:

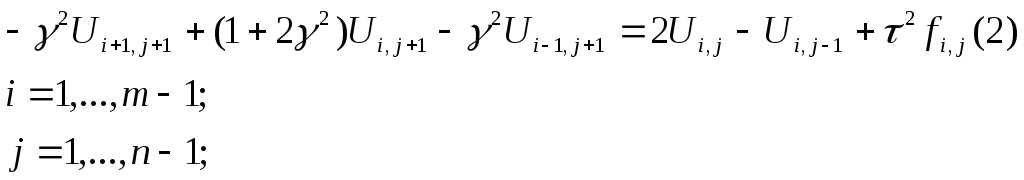
3.2 Аппроксимация 1-го начального условия

(3)

3.3 Аппроксимация 1-го граничного условия

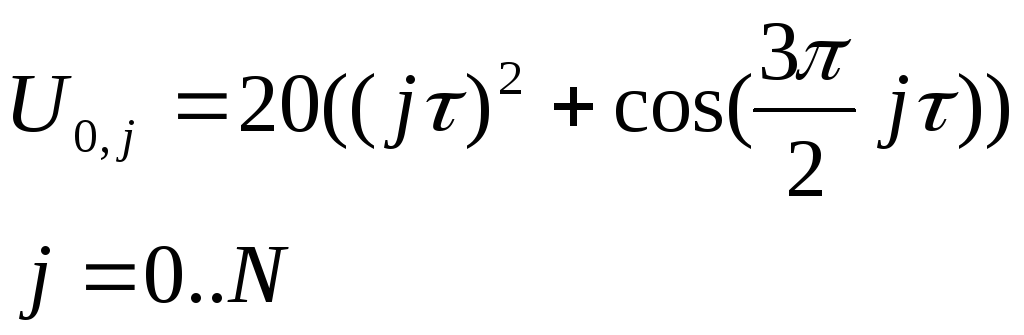(4)

3.4 Аппроксимация 2-го начального условия

Для более точного аппроксимирования 2-го начального условия разложим в окрестности точки по формуле Тейлора и используя 1-ое и 2-ое начальное условия перейдем к конечным разностям:

(5)

Эта формула отличается от аналогичной для явной схемы тем, что аппроксимация разностной производной второго порядка по производится на первом слое, а не на нулевом. Запишем (5) к виду удобному для применения метода прогонки:

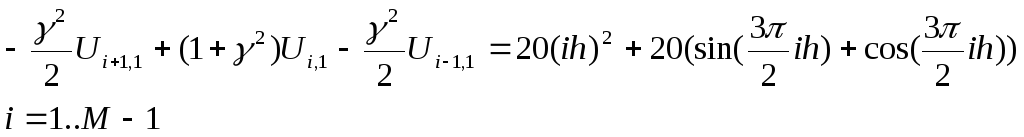(6)

5. Аппроксимация 2-го граничного условия.

При

(7)

При

3.6 Вычисления прогоночных коэффициентов

Сначала найдем на слое . Определим прогоночные коэффициенты.

Учитывая 1-ое граничное условие и уравнение (6) получаем:

a_i = b_i =

C_i = 1 +

f_i =

b₀ = 0, C₀ = 1, f₀ =

Теперь вычислим граничные прогоночные коэффициенты

a_M =0, C_M = 1, f_M = .

Методом прогонки находим где ;

Теперь зная значения находим где

Используя уравнение (2) находим прогоночные коэффициенты:

a_i = b_i =

C_i = 1 +

f_i = 2U_i,j - U_i,j-1

b₀ = 0, C₀ = 1, f₀ = .

Теперь вычислим граничные прогоночные коэффициенты

a_M =0, C_M = 1,

f_M =.

Методом прогонки находим где;

Тексты программ.

Явная схема.

clear

%----------------Число разбиений по осям-------------

M=50; N=55;

%------------------Вычисление шага сетки-------------

h=1/M; t=1/N;

%--------------------Константы-----------------------

u=zeros(M+1,N+1);

g=t/h;

g2=g^2;

t2=t^2;

h2=h^2;

%------------первое граничное условие

for j=0:N,

u(1,j+1)=20*(j*j*t*t+cos(3*pi*j*t/2));

end

%------------первое начальное условие

for i=1:M-1,

u(i+1,1)=20*((i^2)*h2)+20*(sin(3*pi*i*h/2)+cos(3*pi*i*h/2));

end

%%------------заполнение матрицы

for i=1:M-1,

u(i+1,2)=(1-g2)*u(i+1,1)+g2/2*(u(i,1)+u(i+2,1));

end

u(M+1,2)=u(M+1,1)+g2*(u(M,1)-u(M+1,1)+h*(40+30*pi));

for j=1:N-1,

for i=1:M-1,

u(i+1,j+2)=2*(1-g2)*u(i+1,j+1)+g2*(u(i,j+1)+u(i+2,j+1))-u(i+1,j);

end

u(M+1,j+2) =2*(1-g2)*u(M+1,j+1)-u(M+1,j)+2*g2*u(M,j+1)+2*g2*h*(40+30*pi*cos(3*pi*t*j/2));

end;

%-------------------построение графиков-----------

contour(u,40);pause;

mesh(u);pause;

for t=1:60:360

mesh(u,[t,50]);

pause;

end

Неявная схема.

%------ определение числа разбиений по осям x, t -----

M=50; N=60;

%--- определение шагов сетки по оси x или t

h=1/M; t=1/N;

%----------- определение рабочих констант ----------

u=zeros(M+1,N+1);

h2=h^2; t2=t^2; g2=t2/h2;

%-----заполнение матрицы U(x,t) 1-ым начальным условием -

for i=0:M,

u(i+1,1)=20*h2*i^2+20*(sin(3*pi*i*h/2)+cos(3*pi*i*h/2));

end

A=zeros(M,1); C=zeros(M+1,1); B=A; A1=A; F=C; B1=C;

%--- этап заполнения матрицы U(x,t) 2-ым начальным условием

%----------1) Определение прогоночных коэффициентов---------

for i=1:M-1,

A(i)=g2/2;

B(i+1)=g2/2;

C(i+1)=1+g2;

F(i+1)=u(1+i,1);

end;

%-----2) Определение граничных прогоночных коэффициентов----

A(M)=0; B(1)=0; C(1)=1; C(M+1)=1;

F(1)=20*(t^2+cos(3*pi*t/2));

F(M+1)=u(M+1,1)+g2*(u(M,1)-u(M+1,1)+h*(40+30*pi));

%------------ определение U(i,1) методом прогонки ---------

A1(1)=B(1)/C(1); B1(1)=F(1)/C(1);

for i=2:M

A1(i)=B(i)/(C(i)-A(i-1)*A1(i-1));

B1(i)=(F(i)+A(i-1)*B1(i-1))/(C(i)-A(i-1)*A1(i-1));

end;

B1(M+1)=(F(M+1)+A(M)*B1(M))/(C(M+1)-A(M)*A1(M));

u(M+1,2)=B1(M+1);

for i=M:-1:1,

u(i,2)=A1(i)*u(i+1,2)+B1(i);

end;

%------------ этап заполнения матрицы U(x,t) --------------

%-----------1) Определение прогоночных коэффициентов-------

for i=1:M-1, A(i)=g2; B(i+1)=g2; C(i+1)=1+2*g2; end

%-------2) Определение граничных прогоночных коэффициентов--

A(M)=0; B(1)=0; C(1)=1; C(M+1)=1;

%------- определение U(i,j) методом прогонки -------

A1(1)=B(1)/C(1);

for i=2:M,

A1(i)=B(i)/(C(i)-A(i-1)*A1(i-1));

end

for j=2:N,

F(1)=20*((j*j*t*t)+cos(3*pi*j*t/2));

for i=1:M-1,

F(i+1)=2*u(i+1,j)-u(i+1,j-1); end;

F(M+1)=2*g2*(u(M,j)-u(M+1,j)+40*h+30*pi*h*cos(3*pi/2*t*(j-1)))-u(M+1,j-1)+2*u(M+1,j);

B1(1)=F(1)/C(1);

for i=2:M,

B1(i)=(F(i)+A(i-1)*B1(i-1))/(C(i)-A(i-1)*A1(i-1));

end;

B1(M+1)=(F(M+1)+A(M)*B1(M))/(C(M+1)-A(M)*A1(M));

u(M+1,j+1)=B1(M+1);

for i=M:-1:1,

u(i,j+1)=A1(i)*u(i+1,j+1)+B1(i);

end;

end;

%---------построение графиков--------------

contour(u,40);

pause;

mesh(u);

pause;

for t=1:60:360

mesh(u,[t,0]);

pause;

end;

Результаты работы.

Явная схема.

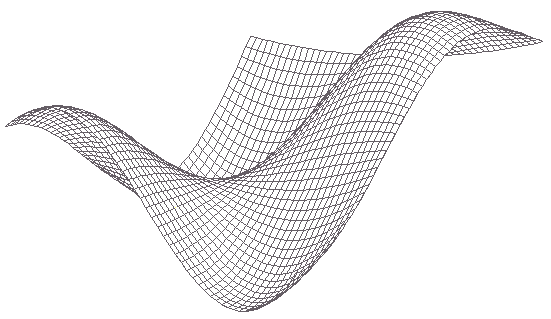
Неявная схема

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ :

1. В.Г. Долголаптев, В.Н. Земсков. Численные методы решения разностных

уравнений математической физики. Методические указания к курсовой работе

по высшей математике., МИЭТ 1987.

2. В.Н. Земсков, С.Я. Хахалин. Метод сеток. Методические указания к выоплнению курсовой работы на персональном компьютере., МИЕТ 1998.