Московский Государственный Институт

Электронной Техники

(Технический Университет)

Курсовая работа

по курсу:

“Численные методы”

на тему:

“Приближённое решение краевых

задач математической физики.

Метод сеток”

Вариант

23

Выполнил: Савицкий Ф.Ф.

Группа МП-38

Проверила: Лисовец Ю.П.

Москва

2003

Постановка задачи и её физическая интерпретация.

Найти с помощью разностных методов решение дифференциального уравнения в частных производных:

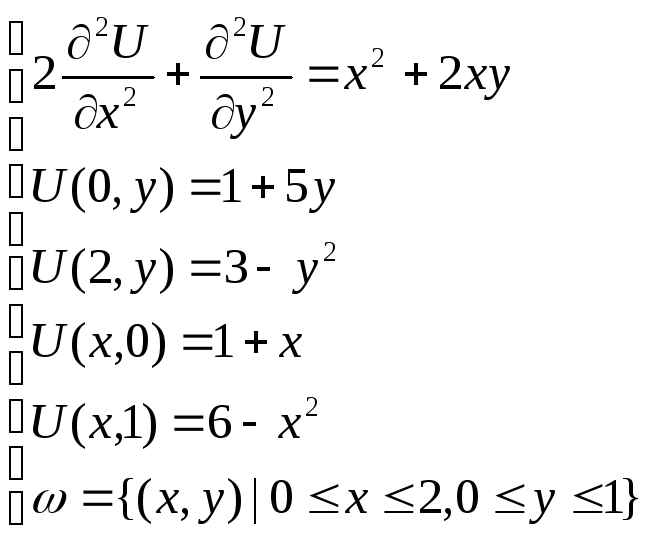
Здесь стоит обратить внимание, что в условиях моей задачи, во 2-ом уравнении, стоит , но с математической точки зрения некорректно, а взял на смелость изменить “u” на “y”. Аналогично я изменил и в 3-ем уравнении, где было

Данное уравнение относится к уравнениям эллиптического типа.

Исследование стационарных процессов различной физической природы часто приводит к необходимости решать уравнения эллиптического типа. Простейшим и наиболее распространенным уравнением эллиптического типа является уравнение Пуассона:

Однородное уравнение Пуассона (при f(x,y)=0) называется уравнением Лапласа. Таким уравнением описываются явления электростатики и агнитостатики. В частности, подобным уравнением описывается потенциал U(x,y) электрического поля, образованного объемным зарядом частиц плотностью f(x,y).

Подобной же установке удовлетворяет задача стационарного двумерного распределения температуры в пластине конечной толщины, если внутри пластины распределены по заданному закону источники (стоки) тепла, описываемые функцией f(x,y) , a на границах поддерживается заданная температура.

Данное уравнение можно интерпретировать как описание распределения температуры в пластине конечной толщины, на всех краях которой поддерживается постоянная во времени температура.

Решение

Для удобства при решении надо преобразовать данную систему следующим образом , тогда система запишется так:

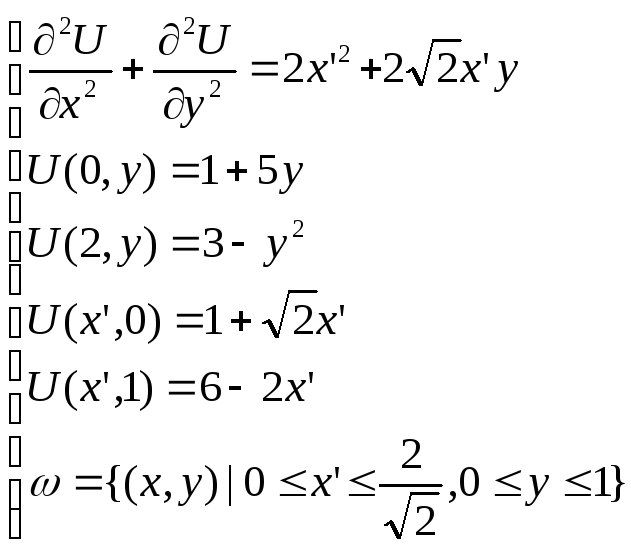
Применение метода сеток при решении уравнения Пуассона.

Метод сеток состоит в сведении решения краевой задачи к решению системы алгебраических уравнений для так называемой сеточной функции. Для этого область непрерывного изменения аргумента заменяется областью дискретного его изменения _h. Дифференциальный оператор заменяется некоторым разностным оператором. Краевые и начальные условия заменяются на соответствующие разностные аналоги. Выберем в области, где ищется решение дифференциального уравнения, некоторое конечное множество точек, в которых мы будем искать решение уравнения. Ясно, что чем больше мы возьмем таких точек, тем точнее решим уравнение. Множество таких точек называется сеткой, отдельные точки - узлами сетки. Функция, определенная в узлах сетки, называется сеточной функцией.

Пусть дан линейный дифференциальный оператор L, действующий на функцию u=u(x,y). Заменяя входящими в L и производные разностными отношениями, получим вместо L u разностное выражение L_h u_h, являющееся линейной комбинацией значений сеточной функции u_h на некотором множестве узлов сетки, называемом сеточным шаблоном. Такая приближенная замена L u на L_h u_h называется аппроксимацией дифференциального оператора разностным оператором.

Говорят, что L_h аппроксимирует дифференциальный оператор L с порядком аппроксимации m >0 в точке x, если

(x)=L_hu(x)-Lu(x)=o(h^m).

Аппроксимируем данное уравнение, используя пяти точечный шаблон "крест". Аппроксимация дифференциального оператора на этом шаблоне имеет вид: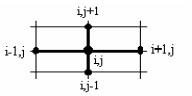

где h1 - шаг сетки по i,

h2 - шаг сетки по j.

Погрешность аппроксимации

.

Если известна искомая функция U(x,y) в точках: (i-1,j); (i+1,j); (i,j+1); (i,j-1),

то значение U(x,y) в точке (i,j), для нашей функции, может быть приближенно найдено следующим образом:

где .

Это уравнение должно выполняться для всех внутренних узлов сетки. Для того чтобы система стала полностью определенной надо дополнить ее уравнениями, полученными при аппроксимации начальных и граничных условий. Их легко получить из исходного уравнения пологая: и , тогда

U_0,j =; U_i,0 =;

U_M,j=; U_i,N=,

для i=1..M-1, j=1..N-1.