Билеты Михайлов / 11

Параллельное соединение активного, индуктивного и ёмкостного элементов

Рассмотрим электрическую цепь, схема замещения которой показана на рис. 3.10. Цепь состоит из трех параллельных ветвей. Общим для всех ветвей является напряжение, приложенное к цепи.

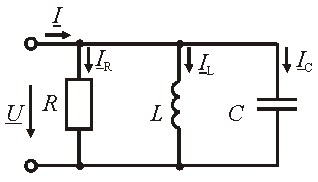Рис. 3.10 – Схема замещения параллельной цепи R, L, C

Пусть заданы напряжение U, параметры R, L, C и частота f. Требуется определить все токи и построить векторную диаграмму. Токи в ветвях соответственно равны (расчёт проводим в комплексной форме)

где комплексные сопротивления ветвей соответственно равны

Z₁ = R₁, Z₂ = jωL = jX_L, Z₃ = - j1/ωC = - jX_C.

Общий ток согласно первого закона Кирхгофа

I = I_R + I_L + I_C.

Построение векторной диаграммы токов и напряжения для параллельной цепи удобно начинать с построения вектора напряжения U. Этот вектор проводим совпадающим с положительным направлением действительной оси + 1. (Вообще вектор напряжения откладывают в произвольном направлении). Этот вектор является базовым вектором.

Вектор тока I_R совпадает по фазе с напряжением; вектор тока I_L через индуктивность отстает от напряжения на угол 90°; вектор тока I_С через ёмкость опережает напряжение на угол 90°. Условно принимаем, что I_L<I_С.

Геометрическая сумма трех векторов токов I_R, I_L, I_С даёт вектор тока в неразветвлённый части цепи. Этот вектор I опережает вектор приложенного к цепи напряжения на угол φ. В этом случае говорят об ёмкостном характере нагрузки в цепи. В построенной диаграмме можно выделить треугольник ОАВ, называемый треугольником токов. Отдельно он показан на рис. 3.11, б. Сторона О₁В₁ называется активной составляющей тока, сторона А₁В₁ – реактивной составляющей тока. Из треугольника токов получаем модуль полного тока

где

I_Х = I_L + I_С.

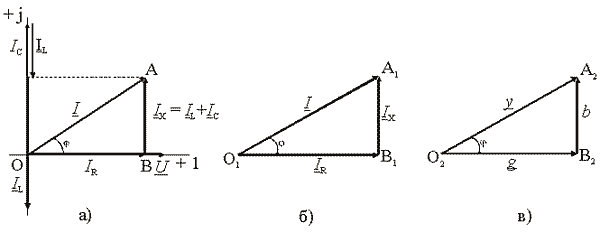Рис. 3.11 а) векторная диаграмма для параллельной цепи R, L, C б) треугольник токов; в) треугольник проводимостей

Выражения для составляющих токов и угла φ

I_R = I·cosφ, I_X = I·sinφ, .

Разделив стороны треугольника токов на напряжение, получим треугольник проводимостей О₂А₂В₂, рис. 3.11, в. В нем сторона О₂В₂ представляет активную проводимость сторона А₂В₂ – реактивную проводимость а гипотенуза О₂А₂ представляет полную комплексную проводимость

у = g + jb,

а ее модуль

Обычно проводимостями пользуются при преобразовании сложных электрических цепей в более простые.

2 Переходные процессы в электрических цепях. Короткое замыкание в цепи с резистором и катушкой

Общая характеристика переходных процессов

В электрических цепях возможны включения и отключения отдельных ветвей, короткие замыкания участков цепи, различного рода переключения. Любые изменения в электрических цепях можно представить в виде переключений или коммутаций. Характер коммутации указывается в схеме с помощью рубильника со стрелкой. По направлению стрелки можно судить, замыкается или размыкается рубильник. При коммутации в цепи возникают переходные процессы, т.е. процессы перехода токов и напряжений от одного установившегося значения к другому. Изменения токов и напряжений вызывают одновременное изменение энергии электрического и магнитного полей, связанных с элементами цепи - емкостями и индуктивностями. Однако энергия электрического поля и энергия магнитного поля могут изменяться только непрерывно, так как скачкообразное изменение потребовало бы от источника бесконечно большой мощности. На этом рассуждении основаны законы коммутации.

Первый закон. В любой ветви с индуктивностью ток не может изменяться скачком и в момент коммутации сохраняет то значение, которое он имел непосредственно перед моментом коммутации

i_L (0₊) = i_L (0_-),

где i_L (0₊) - ток в ветви с индуктивностью в момент коммутации, сразу после коммутации. Знак "+" в формуле обычно не записывается. Время переходного процесса отсчитывается от момента коммутации; i_L (0_-) - ток в индуктивности непосредственно перед коммутацией.

Второй закон. Напряжение на емкости сразу после коммутации сохраняет то значение, которое оно имело непосредственно перед моментом коммутации.

u_C (0₊) = u_C (0_-),

где u_C (0₊) - напряжение на емкости в момент коммутации; u_C (0_-) - напряжение на емкости непосредственно перед моментом коммутации.

Допущения, применяемые при анализе переходных процессов.

1. Полагают, что переходный процесс длится бесконечно большое время.

2. Считают, что замыкание и размыкание рубильника происходит мгновенно, без образования электрической дуги.

3. Принимают, что к моменту коммутации предыдущие переходные процессы в цепи закончились.

В соответствии с классическим методом расчета, переходный ток в ветви схемы представляют в виде суммы принужденного и свободного токов.

.

где i_пр(t) - принужденный ток, определяется в установившемся режиме после коммутации. Этот ток создается внешним источником питания. Если в цепь включен источник постоянной ЭДС, принужденный ток будет постоянным, если в цепи действует источник синусоидальной ЭДС, принужденный ток изменяется по периодическому, синусоидальному закону; i_св(t) - свободный ток, определяется в схеме после коммутации, из которой исключен внешний источник питания. Свободный ток создается внутренними источниками питания: ЭДС самоиндукции индуктивности или напряжением заряженной емкости. Свободный ток определяют по формуле:

.

Количество слагаемых в формуле равно числу реактивных элементов (индуктивностей и емкостей) в схеме. P₁, P₂ - корни характеристического уравнения. А₁, А₂ - постоянные интегрирования, определяются с помощью начальных условий. Начальные условия - это переходные токи и напряжения в момент коммутации, в момент времени t, равный нулю. Начальные условия могут быть независимыми или зависимыми. Независимыми называют начальные условия, подчиняющиеся законам коммутации, законам постепенного, непрерывного изменения. Это напряжение на емкости u_c(0) и ток в ветви с индуктивностью i_L(0) в момент коммутации. Остальные начальные условия: напряжение и ток в ветви с сопротивлением u_R(0) и i_R(0), напряжение на индуктивности u_L(0) , ток в ветви с емкостью i_C(0) - это зависимые начальные условия. Они не подчиняются законам коммутации и могут изменяться скачком.

Короткое замыкание в цепи с резистором и катушкой

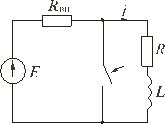Рис. 5.2

Исследуем электромагнитные процессы в цепи, изображенной на рис. 5.2, происходящие после замыкания ключа.

Рассчитаем установившийся режим в цепи до коммутации (до замыкания ключа) и определим из него независимое начальное условие — ток в катушке в момент t = 0_-, непосредственно предшествующий коммутации

i(0_-) = i(0₊) = E / (R_вн + R).

Найдем установившийся ток i после коммутации. Так как во вновь образованном контуре из катушки L и резистора R нет источника, то i_y = 0.

Для определения свободной составляющей тока запишем по второму закону Кирхгофа уравнение электрического состояния цепи после коммутации:

.

Характеристическое уравнение имеет вид:

pL + R = 0.

Общее решение уравнения для свободной составляющей:

i_св = A e^pt,

где: А – постоянная интегрирования; p = - R/L, c^-1 – корень характеристического уравнения.

Записав общий вид переходного тока катушки

i = i_у + i_св = A e^pt,

приравниваем его значение i(0₊) = A в точке t = 0₊ к значению i(0_-), найденному в п. 1. Получаем искомую константу

A = E / (R_вн + R) = I₀.

Переходный ток i = i_у + i_св при этом равен

,

где τ = L / R – постоянная времени цепи.

Постоянная времени – это время, в течение которого свободная составляющая процесса уменьшается в е = 2,72 раза по сравнению с начальным значением.

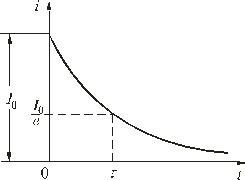Рис. 5.3

График изменения переходного тока показан на рис. 5.3.

Определим э.д.с. самоиндукции катушки

t ≥ 0.

В момент коммутации эта э.д.с. равна напряжению на сопротивлении R, а в дальнейшем уменьшается по экспоненциальному закону. На основании изложенного можно сделать следующие выводы.

1. При коротком замыкании в рассматриваемой цепи ток в ней изменяется по экспоненциальному закону, уменьшаясь от начального значения до нуля.

2. Скорость изменения тока определяется постоянной времени цепи, которая равна индуктивности катушки, деленной на активное сопротивление цепи.

3. Практически можно считать, что переходный процесс заканчивается при t ≈ (3…5)τ , когда первоначальное значение тока уменьшается по модулю на порядок.

4. Напряжение на катушке в начальный момент времени равно напряжению на активном сопротивлении:

u_L(0₊) = I₀R.

5. С энергетической точки зрения рассматриваемый переходный процесс характеризуется расходом энергии магнитного поля катушки на тепловые потери в резисторе. Следует отметить, что сопротивление резистора влияет не на количество выделенной теплоты W, а на начальное значение напряжения катушки и длительность процесса. В самом деле