
ТЦС / 3-лаб
.pdf3 Лабораторная работа №3
Сверточное кодирование. Код Рида-Соломона
3.1 Цель работы
Изучение методов построения кодеров и декодеров сверточных кодов, кода Рида-Соломона.
3.2 Предварительная подготовка
3.2.1Изучить методы кодирования и декодирования сверточных кодов.
3.2.2Изучить технические средства, применяемые при кодировании и декодировании сверточных кодов.
3.2.3Изучить возможности обнаружения и исправления ошибки сверточных кодов.
3.2.4Изучить методы кодирования и декодирования кодов Рида-
Соломона.
3.3 Рабочее задание
3.3.1 Исследовать кодирующее и декодирующее устройство сверточного кода.
3.3.2 Исследовать кодирующее устройство кода Рида-Соломона, исправляющее ошибки.
3.4 Методические указания по выполнению работы
3.4.1Исследование кодера сверточного кода
Всверточном коде блок из n символов кода, формируемых кодером в любой выбранный интервал времени, зависит не только от k информационных символов, поступивших на его вход в течение этого же интервала времени, но и от информационных символов, поступивших в течение (K-1) предыдущих интервалов. Параметр K называется длиной кодового ограничения. Для сверточных кодов значение параметров n и k выбираются малыми. Сверточные коды могут использоваться для исправления случайных ошибок, ошибок, группирующихся в пакеты, и для тех и других. Кодер двоичного сверточного кода содержит kK-разрядный регистр и n сумматоров по модулю 2. Обобщенная структурная схема кодера сверточного кода приведена на рисунке 3.1.

Рисунок 3.1 – Обобщенная структурная схема кодера сверточного кода
На рисунке 3.2 приведены пример кодера сверточного кода с параметрами k=1, n=2, K=3, Rk=1/2. Информационные символы поступают на вход регистра, а символы кода формируются на выходе коммутатора. Коммутатор (КМ) последовательно опрашивает выходы сумматоров по модулю 2 в течение интервала времени, равного длительности информационного символа (бита).
Рисунок 3.2 – Структурная схема кодера несистематического сверточного кода со скоростью1/2
Процедуры кодирования и декодирования удобно описывать с помощью так называемого кодового дерева, которое отображает
последовательности на выходе кодера для любой возможной входной последовательности. На рисунке 3.3 приведено кодовое дерево кодера, изображенного на рисунке 3.2, для блока из пяти информационных символов. Если первый символ принимает значение 0, то на выходе кодера формируется пара символов 00. Если первый символ принимает значение 1, то на выходе кодера формируется пара символов 11. Это показано с помощью двух ветвей, которые выходят из начального узла. Верхняя ветвь соответствует 0, нижняя – 1. В каждом из последующих узлов ветвление происходит аналогичным образом: из каждого узла исходит две ветви,
2

причем верхняя ветвь соответствует 0, а нижняя – 1. Ветвление будет происходить вплоть до последнего символа входного блока. Вслед за ним все входные символы принимают значение 0, и образуется только одна обрывающаяся ветвь. Таким образом, каждой из возможных входных
комбинаций информационных символов соответствует своя вершина на кодовом дереве. В данном случае имеется 32 вершины. С помощью кодового дерева легко построить выходную последовательность символов кода, соответствующую определенной входной последовательности. Например, входной последовательности 11010 соответствует выходная последовательность, лежащая на пути, изображенном пунктирной линией. Анализируя структуру кодового дерева на рисунке 1.3, можно заметить, что, начиная с узлов третьего уровня, она носит повторяющийся характер. Действительно, группа ветвей, заключенных в прямоугольники, изображенные пунктирными линиями, полностью совпадают. Это означает,
что при поступлении на вход четвертого символа выходной символ кода будет одним и тем же, независимо от того, каким был первый входной символ: 0 или 1. Другими словами, после первых трех групп выходных символов кода входные последовательности 1х1х2х3х4… и 0х1х2х3х4… будут порождать один и тот же выходной символ.
Рисунок 3.3 – Кодовое дерево для кодера, изображенного на рисунке 3.2
3

3.4.1.1 Соберите схему simple_coder.svu (рисунок 3.3)
Рисунок 3.3 – Система simple_coder.svu
В данном примере сверточный кодер реализован с использованием дискретных компонентов и стандартного сверточного кодера SystemView.
а) Для входной последовательности 101000 определите, каким будет выход через «ручное» вычисление либо из эквивалентной схемы или от использования диаграммы состояния, предположите, что кодеры пускаются в режиме 00;
б) Перед запуском системы проследите, чтобы норма осуществления
выборки  была установлена на 19,2 Гц, а данные являются входными по норме 9,6 кбит после downsampler. Следовательно, кодер принимает данные в 9,6 kbit/s при 19,2 kbit/s на выходе. Обратите внимание, что символические параметры подтверждают, что это правильно;
была установлена на 19,2 Гц, а данные являются входными по норме 9,6 кбит после downsampler. Следовательно, кодер принимает данные в 9,6 kbit/s при 19,2 kbit/s на выходе. Обратите внимание, что символические параметры подтверждают, что это правильно;
в) Запустите систему, и отметьте закодированный выход для данного входа.
Проследите, чтобы символ стандартного сверточного кода имел время ожидания двух бит перед дискретным выполнением; это просто функция символического проектирования. Также обратите внимание, что «полиномиалы» кодера удобно представлены октальными величинами, т.е. {78 58} = {111 101}.
Параметры для схемы Сверточный код приведены в приложении Б.
4

3.4.1.2 Соберите схему simple_coder(2 variant).svu (рисунок 3.4)
Рисунок 3.4 – Система simple_coder(2 variant).svu
Проделайте аналогичные действия, как и в предыдущем упражнении. Параметры для схемы Сверточный код (2 вариант) приведен в
приложении Б.
3.4.2 Исследование декодеров сверточного кода
Среди различных алгоритмов декодирования сверточных кодов алгоритм максимального правдоподобия Витерби получил наиболее широкое распространение в системах связи, в которых необходимо обеспечить экономию энергетического ресурса.
При декодировании в соответствии с критерием максимального правдоподобия выбирается то кодовое слово из множества возможных,
которое ближе всего располагается к принятому кодовому слову в пространстве кодовых слов. Поскольку имеется 2К кодовых слов, то при
реализации алгоритма максимального правдоподобия необходимо обеспечить запоминание всех кодовых слов и их сравнение с принятым словом. С увеличением К сложность вычислений и, следовательно, декодера возрастают.
Обратимся к решетчатой диаграмме, изображенной на рисунке 3.5. Задача состоит в том, чтобы для некоторой принятой последовательности символов найти путь на решетчатой диаграмме, соответствующий выходной последовательности символов, в максимальной степени совпадающей с принятой последовательностью.
5

Рисунок 3.5 – Решетчатая диаграмма для кодера, изображенного на рисунке 3.2
Предположим, что первые шесть символов последовательности есть 01 00 01. Рассмотрим два пути, состоящих из трех ветвей (для шести символов) и заканчивающихся в узлах a, b, c и d. Из двух путей сохраним лишь тот,
который в максимальной степени согласуется с последовательностью 01 00 01 (путь с минимальным расстоянием). Оставшийся для каждого узла такой путь будем называть «выжившим».
Имеется два пути в узел третьего уровня a: 00 00 00 и 11 10 11. Эти пути имеют расстояния от принятой последовательности 01 00 01, равные соответственно 2 и 3. Выжившим путем вычисления расстояния следует считать путь 00 00 00. Процедуру повторим для узлов b, c и d. Например, для узла c имеются два пути, соответствующих выходным последовательностям 00 11 10 и 11 01 01 и имеющих расстояния, соответственно 5 и 2. Выжившим следует считать путь 11 01 01. Аналогичным образом производится отбор выжившим путей для узлов b и d. В результате из восьми возможных путей сохраняются только четыре. Причина, по которой отбрасываются четыре пути, состоит в следующем. Два пути, сходящиеся, например, в узле третьего уровня a, имеют два одинаковых первых символов, оба пути должны сойтись именно в этом узле a и в будущем выродиться в один.
Таким образом, необходимо запомнить четыре выживших пути и их расстояние от принятой последовательности. В общем случае количество выживших путей равно количеству состояний, т.е. 2К-1.
Теперь рассмотрим два очередных принятых символов. Допустим принимается последовательность символов 01 00 01 00. Сравним два выживших пути, которые сходятся в узле a четвертого уровня. Они могут выходить только из узлов a и c третьего уровня и соответствовать последовательностям 00 00 00 00 и 11 01 01 11, которые имеют расстояния, соответственно равные 2 и 4 от принятой последовательности 01 00 01 00. Следовательно, путь 00 00 00 00 следует считать выжившим для узла a четвертого уровня. Далее аналогичная процедура отбора повторяется для узлов b, c и d.
6

Отметим, что до окончания декодирования сохраняются только четыре конкурирующих пути, которые соответствуют выжившим путям для узлов b, c и d. Остается решить вопрос, когда произвести усечение алгоритма и принять решение в пользу одного из четырех оставшихся путей. Это можно сделать принудительно, положив последние два информационных символа равными 00, т.е. осуществить сброс. При поступлении на вход регистра первого символа 0 необходимо рассматривать выжившие пути только для узлов a и c, поскольку переход в узлы b и d возможен только при поступлении на вход символа 1. При поступлении на вход регистра второго символа 0 необходимо рассмотреть только выжившие пути, сходящиеся в узле a, поскольку при поступлении символов 00 декодер должен перейти в состояние a.
При реализации алгоритма Витерби объем памяти и сложность вычислений пропорциональна 2К, поэтому его целесообразно использовать при длине кодового ограничения К<10. При больших длинах кодового ограничения, которые необходимы для достижения низких значений вероятности ошибки, обычно используется алгоритм последовательного декодирования.
3.4.2.1 Соберите схему conv_coder_decoder.svu (рисунок 3.6)
Рисунок 3.6 – Система conv_coder_decoder.svu
В этом примере использован тот же кодер (7,5), что и в предыдущем задании, и сверточный декодер, или декодер Витерби, длиной дорожки 15.
а) Запустите систему и убедитесь, что последовательность на выходе декодирована правильно. Заметьте, что имеется время ожидания 17 бит. Как вы это объясните?
б) Запустите систему и отметьте кодированный выход для данного входа. Проследите, чтобы символ стандартного сверточного кодера имел
7
время ожидания двух бит перед выполнением. Это просто функция символического проектирования.
Параметры для схемы Сверточное кодирование/ декодирование приведены в приложении Б.
3.4.3 Исследование кода Рида – Соломона, исправляющего ошибки
Рассматривая основные двоичные коды, исправляющие ошибки, очевиден недостаток этих кодов – малая загруженность линии связи. Действительно, через линию проходит только два сигнала: сигнал “0” и сигнал “1” , в то же время как возможности линии допускают гораздо меньшую дискретность и большее количество дискретных уровней.
Наличие ошибок, обусловленных помехами в каналах передачи, а также физическими повреждениями носителей в каналах хранения, требует введения избыточности в информацию, подлежащей передачи и хранению.
Помехоустойчивая обработка двоичной информации кодов с основанием 2а позволяет получить достаточно простые реализации
кодирующих и декодирующих устройств при высокой исправляющей и обнаруживающей способностях как в отношении независимых, так и корректированных ошибок. К ним относятся линейные блоковые коды с основанием 2а
Коды Рида – Соломона, или РС-коды, относятся к недвоичным циклическим кодам, т. е. кодам, символы которых взяты из конечного поля, содержащего q > 2 элементов и обозначаемого GF(q), где q – степень некоторого простого числа.
Пусть необходимо передать по каналу связи последовательность из M двоичных элементов вида: 111 … 1 101 … 1 011 … 0 100 … 1.Разобьем эту последовательность на блоки по m элементов и обозначим их через некоторые символы b0, b1, b2, …, bN–1, где N=M/m. Полное число различных значений m-элементных блоков равно q=2m.
Таким образом, передаваемая последовательность представляется в виде некоторой q-ичной последовательности: b0, b1, …, bS, …bN-1.
Некоторая совокупность q-ичных последовательностей образует q- ичный код. Такие коды, как и двоичные коды, могут быть простыми и помехоустойчивыми.
Кодовые комбинации q-ичного кода могут быть представлены в виде многочленов с q-ичными коэффициентами – элементами поля GF(q). При этом q-ичные коэффициенты как элементы поля GF(q) являются в рассмотренном примере многочленами с двоичными коэффициентами.
Например:
B(x) = b0 (z)x 0 + b1 (z)x1 + ... + bN−1x N−1 , |
(3.1) |
где bi (z) = b0z0 + b1z1 + ... + bm−1xm−1.
8
Здесь bi=0,1, а z – формальная переменная многочлена с двоичными коэффициентами.
Кодом Рида-Соломона (РС - кодом) называют циклический (N,K)-код, при N = q–1, множество кодовых комбинаций которого представляется многочленами степени N–1 и менее с коэффициентами из поля GF(q), где q > 2 и является степенью простого числа, а корнями порождающего многочлена являются N–K последовательных степеней: a, a2, a3, …, aD–1, некоторого элемента a О GF(q), где D – минимальное кодовое расстояние (N,K)-кода.
Из определения вытекает, что РС-код является подклассом БЧХ - кодов с m0 = 1. Обычно считают элемент a примитивным элементом поля GF(q), т. е. все степени a от 1-й до (q–1)-й являются всеми различными ненулевыми элементами поля GF(q). Порождающий многочлен РС - кода имеет степень N–K = D–1 и по теореме Безу может быть найден в виде произведения
D−1 |
|
g(x) = ∏(x − α i ) |
(3.2) |
i=1
Всоответствии с теорией циклических кодов, порождающий
многочлен g(x) является делителем xN–1 над GF(q).
Таким образом, РС-код над полем GF(q) имеет длину кодовой комбинации N = q–1, число избыточных элементов в ней N–K = D–1 и минимальное кодовое расстояние D = N–K+1.
Коды с подобным значением минимального кодового расстояния в теории кодирования получили название максимальных.
При фиксированных N и K не существует кода, у которого минимальное кодовое расстояние больше, чем у РС-кода. Этот факт часто является веским основанием для использования РС-кодов. В то же время РС-
коды всегда оказываются короче всех других циклических кодов над тем же алфавитом. РС-коды длины N<q–1 называют укороченными, а коды длины q (или q+1) – расширенными (удлиненными) на один (или два) символа.
Коды Рида – Соломона обладают всеми свойствами линейных кодов, следовательно, за счет этого можно строить порождающие и проверочные матрицы.
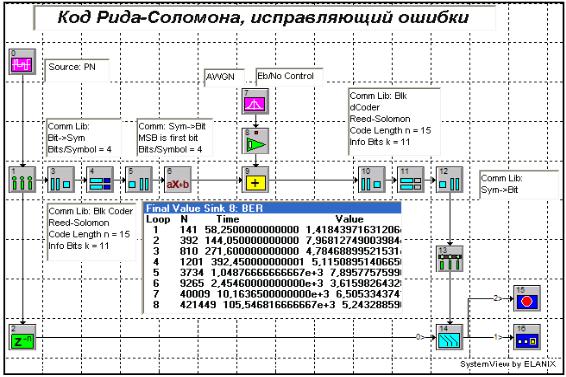
3.4.3.1 Откройте систему reed – Solomon.svu (рисунок 3.7)
Это упражнение демонстрирует BER представление ошибки исправления кода Рида – Соломона
В этом упражнении используется BER значок из Библиотеки Связи, который был спроектирован для изменения частоты ошибок на бит.
а) Сколько бит на входе необходимы, чтобы получить символ для кодирующего устройства? Модуляция – основная полоса частот диаметрально противоположная сигнализации. Поэтому кодируемые символы должны быть обратно преобразованы в биты;
б) Рассмотрите процесс моделирования еще раз, чтобы понять как действует каждый значок. Значок источника шума установлен в 0,25 W/Hz. Каково соответствующее ему значение Eb/N0;
9
в) Запустите файл упражнения. Переместитесь в окно анализа, чтобы рассмотреть кривую BER. Какое Вы можете сделать заключение насчет эффективности кода когда значение Eb/N0 является сравнительно высоким?
Параметры для схемы кода Рида – Соломона приведены в приложении
Б.
Рисунок 3.7 – Система reed – Solomon.svu
3.5 Контрольные вопросы
3.5.1Какие коды называют помехоустойчивыми?
3.5.2За счет чего помехоустойчивый код получает способность обнаруживать и исправлять ошибки?
3.5.3Назовите основные структуры сверточных кодов.
3.5.4Основные применения сверточных кодов.
3.5.5Кокой характерной особенностью обладают сверточные коды?
3.5.6Объясните алгоритм декодирования Витерби.
3.5.7Какие коды называют кодами Рида – Соломона?
3.5.8В качестве чего используются коды Рида – Соломона?
3.5.9Перечислите основные достоинства и недостатки, а также свойства кодов Рида – Соломона.
10
