Методички / Вектор.Алг.в.электр

4)A 4; 0;3 , B 2;3;5 , C 6; 2; 1 ;

5)A 2; 1; 7 , B 5; 4;3 , C 0;1; 2 ;

6)A 1; 2;1 , B 1; 4; 5 , C 6; 3;1 ;

7)A 3; 5; 4 , B 1; 4; 2 , C 2;1; 0 ;

8)A 5; 2; 4 , B 3; 1; 3 , C 0; 6; 2 ;

9)A 7; 0; 2 , B 5; 3;1 , C 2; 4;8 ;

10)A 1; 2; 4 , B 2;3; 5 , C 7;1; 6 .

3.4.Найти m n .

3.5. Являются ли векторы коллинеарными или ортогональными ?

10) a 4i 2j 3k , b 2i k .

3.6.При каком значении , точки A, B, C, D лежат в одной

плоскости?

1)A 4; 6;3 , B 5; ; 6 , C 4; 4; 3 , D 1;3; 2 ;

2)A ; 4; 5 , B 1; 2;3 , C 1; 2; 4 , D 1;3; 5 ;

3)A1; 4; 3 , B 2; 3;1 , C 0; ;5 , D 2; 3; 4 ;

4)A 3; 1; 4 , B 2; ;1 , C 2; 2; 4 , D 1;3; 2 ;

5)A1; 4; 2 , B 1; 3; , C 2; 4; 1 , D 2; 3;1 ;

6)A 3; ; 5 , B 2; 3; 4 , C 2; 4; 0 , D 1; 4;5 ;

7)A1; 4; 2 , B 1; 4;3 , C 3;1; 4 , D 1; 2; ;

21

8)A ; 4; 3 , B 3; 2; 4 , C 0; 0; 2 , D 3; 4; 4 ;

9)A 2; 3; 2 , B 1; ; 4 , C 1; 3;3 , D 5; 6;1 ;

10)A 2; 4; 1 , B 0;3; 5 , C 1; ; 1 , D 5; 7; 3 .

3.7. Установить, компланарны ли векторы a, b, c , в случае их не компланарности выяснить, какую тройку (правую или левую) они образуют, и вычислить объем построенного на них параллелепипеда.

10) a ( 3, 5,1), b (4, 2, 1), c (1, 5, 3).

Прежде чем вычислить модуль векторного произведения, вычислим само произведение векторов.

(m n) (m 2n)

используя свойство дистрибутивности 3. получим

m m m 2n n m n 2n

Используя свойство антикоммутативности 1. и формулу векторного квадрата

(3.2)

m 2n m n 3(m n).

Т.о. мы получили (m n) (m 2n) 3(m n). Вычислим модуль полученного выражения, используя формулу (3.1):

(m n) (m 2n) 3m n 3 2 5 sin 15. 6

22

Для вычисления координат вектора a b будем использовать формулу (3.4):

первой строки:

(2a b) (a 3b), раскроем векторное произведение:

(2a b) (a 3b) 2(a a) 2 3(a b) (b a) 3(b b)

Используя свойство антикоммутативности и векторного квадрата, получим

7(a b) 7 c .

Подставляя в полученное соотношение координаты вектора с, получим:

(2a b) (a 3b) 7с ( 70; 77; 49).

Откуда модуль вектора:

(2a b) (a 3b) 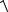( 70)2 ( 77)2 ( 49)2 12930.

3.3. Вычислить площадь параллелограмма построенного на векторах

AB и CB. Высоту, опущенную на сторону, совпадающую с CB. Площадь треугольника ABC, если: A 2; 5; 3 , B 1; 4; 7 , C 1; 2;3 .

Решение:

Площадь параллелограмма, построенного на векторах AB и CB, равна модулю векторного произведения этих векторов (3.1). Вычислим координаты

AB и CB:

AB (1 2; 4 5; 7 ( 3)) ( 1; 1;10);

CB (1 ( 1); 4 ( 2); 7 3) (2; 6; 4).

23

Решение:

По определению, модуль векторного произведения вычисляется по формуле

(3.1): m n m n sin(m,n). Скалярное произведение по формуле (2.1):

m n m n cos(m,n). Тогда выражая косинус и определяя через него синус угла, мы определим модуль векторного произведения.

24

Векторы ортогональны, если их скалярное произведение равно нулю (свойство 5. скалярного произведения). Векторы коллинеарны, если их соответствующие координаты пропорциональны (3.3).

Вычислим скалярное произведение векторов а и b :

a b 3 1 ( 6) ( 2) 2 7 29 0 векторы не ортогональны. Проверим условие пропорциональности их координат:

Решение:

Точки лежат в одной плоскости, если построенные на них вектора AB,

АC и AD компланарны. Три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю (3.6). Вычислим координаты