
5. Практикум
1.
Для данной матрицы
 вычислить определитель:
вычислить определитель:
1) методом параллельного переноса;
2) методом треугольника;
3)
разложением по
 -ой
строке и по
-ой
строке и по -му
столбцу;
-му
столбцу;
4) вычислить, получив нулевые элементы в первом столбце используя элементарные преобразования со строками;
5)
вычислить обратную матрицу
 .
.
1)
 ,
, , 2)
, 2) ,
, ;
;
3) ,
, , 4)
, 4) ,
, ;
;
5)
 ,
, , 6)
, 6)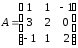 ,
, ;
;
7)
 ,
, , 8)
, 8) ,
, ;
;
9)
 ,
, , 10)
, 10) ,
, .
.
6. Решение типового варианта
Для
данной матрицы
 ,
, вычислить определитель:
вычислить определитель:
1) методом параллельного переноса;
2) методом треугольника;
3)
разложением по
 -ой
строке и по
-ой
строке и по -му
столбцу;
-му
столбцу;
4) вычислить, получив нулевые элементы в первом столбце используя элементарные преобразования со строками;
5)
вычислить обратную матрицу
 и проверить равенство
и проверить равенство
![]() .
.
Решение.
1) Согласно правила параллельного переноса, допишем к нашему определителю две первые строки и сделаем действия согласно схеме (2.3)





 .
.
2) согласно схеме (2.4) вычислим определитель методом треугольников:








 .
.
3) разложением по элементам 2-ой строки:
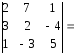

Выпишем миноры и вычислим их:
 ,
, ,
, .
.
Наше разложение по второй строке имеет вид:

 .
.
Разложением по элементам 3-его столбца:


Аналогично предыдущего пункта записываем миноры, вычисляем их, получаем:

 .
.
4) Используя элементарные преобразования со строками, получим нулевые элементы в первом столбце. Для этого:
1) умножим третью строку на (-2) и прибавим к первой строке,
 ;
;
2) умножим третью строку на (-3) и прибавим ко второй строке.
 ;
;
Получили определитель эквивалентный исходному

Полученный определитель разложим по элементам первого столбца


Вычислить обратную
 матрицу
и проверить равенство
матрицу
и проверить равенство

 .
.
Решение:
Вычислим определитель матрицы:
 .
.
 Т.к. определитель отличен от нуля, то
матрица не является вырожденной и для
нее определена обратная матрица. Для
её нахождения протранспонируем матрицу
Т.к. определитель отличен от нуля, то
матрица не является вырожденной и для
нее определена обратная матрица. Для
её нахождения протранспонируем матрицу
 и
вычислим её алгебраические дополнения
по формулам (2.7)
и
вычислим её алгебраические дополнения
по формулам (2.7)

 ;
;
 ;
;
 ;
; ;
; ;
;
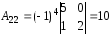 ;
;
 ;
;
 ;
;
 ;
; .
.
Тогда обратная матрица согласно формуле (2.8) запишется в виде:
 .
.
Сделаем
проверку и убедимся, что



Вынесем числовой множитель и перемножим матрицы согласно формуле (1.4)

 .
.
Обратная матрица вычислена верно.
7. Дополнительные задания
1.
Решить уравнение
 ,
если
,
если ,
,
(воспользоваться свойством единичной матрицы).
2.
Решить уравнение:
 .
.
3.
Вычислить определитель:

(воспользоваться свойствами определителя).
4.
Вычислить определитель, приведя его к
треугольному виду:
 .
.
8. Список используемой литературы
Любимова О.Н., Дегтярева Н.Е. Линейная алгебра и аналитическая геометрия. Владивосток.: изд-во ДВГТУ, 2008г. - 167с.
Клиот-Дашинский М.И. Алгебра матриц и векторов. С-Петербург.: изд-во «Лань», 2001г. – 160с.
Оглавление
федеральное агенство по образованию 1
матрицы 1
определители 1
Владивосток 2011 1
Одобрено методическим советом университета 2
1. Матрицы и действия над ними 3
2. Практикум 5
4. Определитель матрицы. Обратная матрица 13
Решение. 18
8. Список используемой литературы 24
матрицы
определители
Методические указания
Составители: Дегтярева Н.Е., Агеева Е.В.
Корректор:
Технический редактор
Подписано в печать . Формат
Печать офсетная. Усл.печ.л. Уч.-изд.л.
Тираж 100 экз. Заказ
__________________________________________________________________
Издательство ДВГТУ.690650, Владивосток, Пушкинская, 10
Типография издательства ДВГТУ, 690650, Владивосток, Пушкинская, 10
