Чет про электрику / ЛР 7.5 Магнитное поле соленоида

Обложка

Исследование магнитного поля соленоида с помощью датчика Холла

Учебно-методическое пособие к лабораторной работе № 7.5 по дисциплине «Физика»

Владивосток

2014

Титул

Министерство образования и науки Российской Федерации

Дальневосточный федеральный университет

Школа естественных наук

Исследование магнитного поля соленоида с помощью датчика Холла

Учебно-методическое пособие к лабораторной работе № 7.5 по дисциплине «Физика»

Владивосток

Дальневосточный федеральный университет

____________________________________________________________________________________________________________

Оборот титула

УДК 53 (о76.5)

ББК 22. 343

Э41

Составитель: О.В.Плотникова

Исследование магнитного поля соленоида с помощью датчика Холла

Учебно-методическое пособие к лабораторной работе № 7.5 по дисциплине «Физика» / Дальневосточный федеральный университет, Школа естественных наук [сост. О.В.Плотникова]. – Владивосток: Дальневост. федерал. ун-т, 2014. - с.

Пособие, подготовленное на кафедре общей физики Школы естественных наук ДВФУ, содержит краткий теоретический материал по теме «Магнитное поле постоянного тока» и инструктаж к выполнению лабораторной работы «Исследование магнитного поля соленоида с помощью датчика Холла» по дисциплине «Физика».

Для студентов-бакалавров ДВФУ.

УДК 53 (о76.5)

ББК 22. 343

©ФГАОУ ВПО «ДВФУ», 2014

Цель работы: изучить магнитное поле длинного соленоида, ознакомиться с сущностью и применением эффекта Холла, построить график зависимости индукции магнитного поля от расстояния до центра соленоида.

Краткая теория

Соленоид представляет собой провод, навитый в виде спирали на цилиндрический каркас (рис.1). В теории электромагнитных явлений большую роль играет воображаемый бесконечно длинный соленоид. Особенностью такого соленоида является то, что его магнитное поле ограничено объемом соленоида и однородно. Можно провести аналогию с бесконечным плоским конденсатором, обладающим такими же свойствами по отношению к электрическому полю.

Силовые линии однородного магнитного поля бесконечно длинного соленоида параллельны его оси , и их направление связано с направлением тока в витках правилом правого винта.

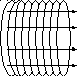В Рис.1

I

Величина магнитной индукции бесконечно длинного соленоида прямо пропорциональна силе тока в нем (I) и числу витков, приходящихся на единицу длины (n): B=μ₀nI,

Где μ₀ – магнитная постоянная.

Данное выражение можно получить, используя теорему о циркуляции (закон полного тока).

Циркуляция вектора магнитной индукции равна интегралу:

, где B_l – проекция вектора магнитной индукции на направление обхода контура.

Теорема о циркуляции: Циркуляция вектора магнитной индукции по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром, умноженной на магнитную постоянную:

= μ₀∑I_i.

Рассмотрим бесконечно длинный соленоид (на рисунке 2 изображена часть соленоида), по которому течет ток I. Выберем замкнутый контур АВCD прямоугольной формы так, чтобы сторона АВ лежала внутри соленоида и была параллельна его оси.

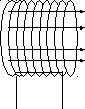Рис.2

Тогда циркуляция вектора В может быть представлена как сумма 4-х интегралов:

== BL, (1)

Где L – длина стороны АВ.

Интегралы по остальным трем участкам выбранного контура обращаются в ноль, так как на этих участках равна нулю либо сама индукция магнитного поля, либо ее проекция на данный участок контура.

Сумма токов, охватываемых данным контуром, равна произведению тока в одном витке на число витков, укладывающихся на отрезке АВ длиной L:

∑I_i= IN=InL (2)

(используем n=N/L).

Подставляя (1) и (2) в выражение теоремы о циркуляции, получим:

BL = μ₀InL, отсюда

В = μ₀In.. (3)

Реальные катушки не являются бесконечно длинными, но если длина соленоида намного больше его диаметра, то на участках, достаточно удаленных от концов соленоида, поле можно считать однородным и использовать для определения индукции формулу (3). Если же длина соленоида ненамного превосходит диаметр, то его поле не будет однородным. Величина и направление магнитной индукции в разных точках будут различны, и чем ближе к концам соленоида – тем неоднородность поля будет проявляться сильнее.

Теория метода

В данной работе магнитное поле соленоида исследуется при помощи датчика Холла. Эффект Холла был открыт в 1879 г Он состоит в том, что если металлическую пластинку, по которой течет постоянный электрический ток, поместить в перпендикулярное к ней магнитное поле, то между гранями, параллельными направлениям тока и поля, возникает разность потенциалов Uн₁  ₂. Возникающая разность потенциалов прямо пропорциональна плотности тока, индукции магнитного поля и толщине пластинки.

UнRbjB, (4)

где b  ширина пластинки, j  плотность тока, В  магнитная индукция, R  коэффициент пропорциональности, получивший название постоянной Холла.

На основе эффекта Холла работают измерительные устройства, называемые датчиками Холла (рис.3).

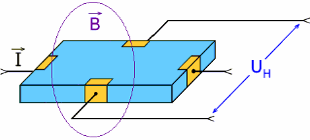
Рис. 3. Датчик Холла

Измеряя напряжение Uн, возникающее в датчике Холла, можно определять индукцию магнитного поля.

Описание установки

Установка состоит из модуля ФПЭ-04, источника питания и мультиметра.

Модуль содержит исследуемый соленоид, по оси которого перемещается шток с находящимся в нем датчиком Холла. На штоке через 10 мм нанесены деления, с помощью которых ведется отсчет перемещения датчика вдоль оси соленоида от его начала (отметка «0» у выхода соответствует положению датчика в центре соленоида). На передней панели модуля имеется разъем, через который подается питание на датчик и снимается сигнал с датчика. Этот сигнал через гнезда PV поступает на мультиметр, измеряющий напряжение Холла. Питание на модуль подается с источника питания через разъем на задней панели модуля.

Порядок выполнения работы

1. Проверьте соединение всех элементов установки. Подключите к гнездам PV мультиметр, установите на нем предел измерения 2В. Шток поместите полностью внутри соленоида (до отметки 100мм).

2. Включите источник питания. Тумблер «Контроль тока» поставьте в правое положение. Установите силу тока соленоида I= 1,5А.

3. Включите мультиметр. Перемещая шток на себя, через каждые 10 мм записывайте величину напряжения Холла Uн. Данные занесите в таблицу.

4. Выключите источник питания (выключатель на передней панели, сетевой шнур), выключите мультиметр и отключите его от модуля.

5. Проанализировав данные измерения, выделите участок, на котором напряжение Холла постоянно. На этом участке поле соленоида можно считать однородным.

6. Определите величину магнитной индукции поля соленоида для выделенного участка, пользуясь формулой (3).

7. Используя значения В и Uн для однородного участка поля, найдите коэффициент К=Rbj, пользуясь формулой (4). Этот коэффициент имеет такое же значение для всех других участков соленоида.

8. Используя полученный коэффициент, найдите величину магнитной индукции для остальных значений : В= Uн/К. Занесите их в таблицу.

9. Постройте график зависимости В от .

При вычислениях используйте следующие данные:

Длина соленоида – 167 мм, общее число витков N=2111.

Таблица

I (А)	1,5
n (м-1)
 (мм)
Uн (В)
В (Тл)

Контрольные вопросы

1. Что называется магнитной индукцией?

2. В чем проявляется вихревой характер магнитного поля?

3. Что называется циркуляцией вектора? Как сформулировать теорему о циркуляции?

4. Что такое соленоид? Каковы особенности поля соленоида?

5. Как находится индукция магнитного поля соленоида?

6. В чем заключается эффект Холла? На чем основан метод использования датчика Холла для исследования магнитного поля?

Концевой титул

Учебное издание

Составитель:

Плотникова Ольга Васильевна

Исследование магнитного поля соленоида с помощью датчика Холла

Учебно-методическое пособие к лабораторной работе № 7.5 по дисциплине «Физика»

В авторской редакции

Компьютерная верстка

Подписано в печать

Формат 60х84/16. Усл.печ.л. Уч.-изд.л.

Тираж экз. Заказ

Дальневосточный федеральный университет

690091, г. Владивосток, ул. Суханова, 8

Отпечатано на кафедре общей физики ШЕН ДВФУ

690091, г. Владивосток, ул. Суханова-8.