2. Конденсаторы.

Емкостью обладают не только отдельные проводники, но и системы проводников. Система, состоящая из двух проводников, разделенных слоем диэлектрика, называется конденсатором. Проводники в этом случае называются обкладками конденсатора. Заряды на обкладках имеют противоположные знаки, но по модулю – одинаковы. Практически все поле конденсатора сосредоточено между обкладками и.

Емкостью конденсатора называется величина

С= , (1)

где q – абсолютная величина заряда одной из обкладок, U - разность потенциалов (напряжение) между обкладками.

В зависимости от формы обкладок, конденсаторы бывают плоскими, сферическими, цилиндрическими.

Найдем емкость плоского конденсатора, обкладки которого имеют площадь S, расположены на расстоянии d, а пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью ε.

Если поверхностная плотность заряда на обкладках равна σ (σ= ), то напряженность поля конденсатора (поле считается однородным) равна:

Е= =

Разность потенциалов между обкладками связана с напряженностью поля: Е = , откуда получим U=Ed = =

Используя формулу ( 1 ), получим для емкости плоского конденсатора выражение:

С = (2)

3. Соединение конденсаторов.

Используются два основных вида соединения: последовательное и параллельное.

При параллельном соединении (рис 1), общая емкость батареи равна сумме емкостей всех конденсаторов:

С_общ.= С₁ +С₂+С₃+…=ΣС_i . (3)

При последовательном соединении (рис.2) величина, обратная общей емкости, равна сумме величин, обратных емкостям всех конденсаторов:

. (4)

Если последовательно соединены n конденсаторов с одинаковой емкостью С, то общая емкость: С_общ.=

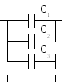
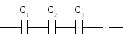
Рис. 1.Параллельное соединение. Рис. 2.Последовательное соединение

4. Энергия конденсатора.

Если процесс зарядки конденсатора является медленным (квазистационарным), то можно считать, что в каждый момент времени потенциал любой из обкладок конденсатора во всех точках одинаков. При увеличении заряда на величину dq совершается работа , где u – мгновенное значение напряжения между обкладками конденсатора. Учитывая, что , получаем: . Если емкость не зависит от напряжения, то эта работа идет на увеличение энергии конденсатора. Интегрируя данное выражение, получим:

,

где W – энергия конденсатора, U – напряжение между обкладками заряженного конденсатора.

Используя связь между зарядом, емкостью конденсатора и напряжением, можно представить выражение для энергии заряженного конденсатора в других видах:

. (5)

5. Квазистационарные токи. Процессы зарядки и разрядки конденсатора.

При зарядке или разрядке конденсатора в цепи конденсатора течет ток. Если изменения тока происходят очень медленно, то есть за время установления электрического равновесия в цепи изменения токов и э.д.с. малы, то для определения их мгновенных значений можно использовать законы постоянного тока. Такие медленно меняющиеся токи называют квазистационарными.

Так как скорость установления электрического равновесия велика, под понятие квазистационарных токов подпадают и довольно быстрые в обычном понимании процессы: переменный ток, многие электрические колебания, используемые в радиотехнике. Квазистационарными являются и токи зарядки или разрядки конденсатора.

Рассмотрим электрическую цепь, общее сопротивление которой обозначим R. Цепь содержит конденсатор емкостью C, подключенный к источнику питания с э.д.с. ε (рис. 3).

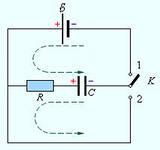
Рис. 3. Процессы зарядки и разрядки конденсатора.

Зарядка конденсатора. Применяя к контуру εRC1ε второе правило Кирхгофа, получим: ,

где I, U – мгновенные значения силы тока и напряжения на конденсаторе (направление обхода контура указано стрелкой).

Учитывая, что , , можно привести уравнение к одной переменной:

.

Введем новую переменную: . Тогда уравнение запишется:

.

Разделив переменные и проинтегрировав, получим: .

Для определения постоянной А используем начальные условия:

t=0, U=0, u= - ε. Тогда получим: А= - ε. Возвращаясь к переменной , получим окончательно для напряжения на конденсаторе выражение:

. (6)

С течением времени напряжение на конденсаторе растет, асимптотически приближаясь к э.д.с. источника (рис.4, I.).

Разрядка конденсатора. Для контура CR2C по второму правилу Кирхгофа: RI=U. Используем также:

, и (ток течет в обратном направлении).

Приведя к переменной U, получим:

. Интегрируя, получим: .

Постоянную интегрирования B определим из начальных условий: t=0, U=ε. Тогда получим: В=ε.

Для напряжения на конденсаторе получим окончательно:

. (7)

С течением времени напряжение падает, приближаясь к 0 (рис. 4, II).

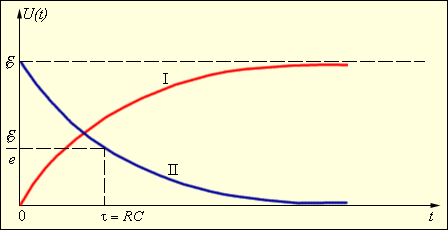
Рис. 4. Графики зарядки (I) и разрядки (II) конденсатора.

6. Постоянная времени. Характер протекания процессов зарядки и разрядки конденсатора (установление электрического равновесия) зависит от величины:

, (8)

которая имеет размерность времени и называется постоянной времени электрической цепи. Постоянная времени показывает, через какое время после начала разрядки конденсатора напряжение уменьшается в e раз (е=2,71).

Теория метода

Прологарифмируем выражение (7):

(учли, что RC=τ).

График зависимости lnU от t (линейная зависимость) выражается прямой линией (рис.5), пересекающей ось y (lnU) в точке с координатами (0; lnε). Угловой коэффициент К этого графика и будет определять постоянную времени цепи: , откуда:

. (9)

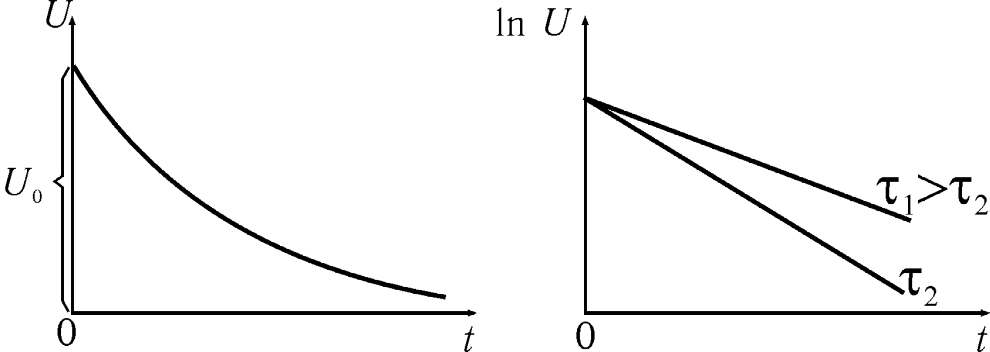
Рис. 5. Зависимость натурального логарифма напряжения от времени при разрядке конденсатора

Используя формулы: и , можно получить, что для одного и того же интервала времени : .

Отсюда: . (10)

Экспериментальная установка

Установка состоит из основного блока – измерительного модуля, имеющего клеммы для подключения дополнительных элементов, источника питания, цифрового мультиметра и набора минимодулей с различными значениями сопротивления и емкости.

Для выполнения работы собирается электрическая цепь в соответствии со схемой, изображенной на верхней панели модуля. В гнезда «R₁» подключается минимодуль с номиналом 1Мом, в гнезда «R₂» - минимодуль с номиналом 100Ом. Параметры исследуемого конденсатора, подключаемого в гнезда «С», задаются преподавателем. В гнезда подключения амперметра устанавливается перемычка. В гнезда вольтметра подключается цифровой мультиметр в режиме вольтметра.

Следует отметить, что сопротивления резисторов заряда-разряда (минимодулей) R и цифрового вольтметра R_V образуют делитель напряжения, что приводит к тому, что фактически максимальное напряжение на конденсаторе будет равно не ε, а ,

где r₀- сопротивление источника питания. Соответствующие поправки необходимо будет вносить и при вычислении постоянной времени. Однако, если входное сопротивление вольтметра (10⁷Ом) значительно превышает сопротивление резисторов, и сопротивление источника мало, то данными поправками можно пренебречь.

Порядок выполнения работы

1. Собрать электрическую цепь с заданным преподавателем значением емкости. Тумблер (переключатель заряда-разряда) установить в среднее положение (стоп). Переключатель предела измерения цифрового мультиметра установить в положение «20В» (режим измерения постоянного напряжения).

2. Подключить модуль к сети переменного тока (клавиша включения на задней панели модуля) и установить выходное напряжение , заданное преподавателем (6,5В-15В). Включить цифровой мультиметр. Нажатием кнопки «Сброс» подготовить модуль к началу измерений.

3. Тумблер перевести в положение «Заряд». При этом запускается секундомер, и начинает меняться напряжение на конденсаторе (показания вольтметра). Довести напряжение на конденсаторе до значения примерно 0,8ε.

4. Сбросить показания секундомера нажатием кнопки «Сброс». Перевести тумблер в положение «Разряд» и измерять напряжения на конденсаторе при его разрядке с интервалом времени 5с. Занести данные в таблицу 1.

5. Подключить в цепь конденсатор с неизвестным значением емкости и повторить измерения по п. 4. Данные занести в таблицу 2.

6. Подключить в цепь конденсатор и резистор с другим известным значением емкости. Повторить измерения по п. 4. Данные занести в таблицу 3.

7. Нажать кнопку «Сброс». Выключить источник питания и мультиметр. Отключить от сети измерительный модуль и отсоединить от него дополнительные элементы.

Таблица 1

ε= В, R1= Ом, , С1= Ф
Разрядка	t (с)
	U (В)
	lnU
τ1±Δτ1 (с)

Таблица 2

ε= В, R1= Ом, Сх=? Ф
Разрядка	t (с)
	U (В)
	lnU
τх±Δτх (с)
Сх±ΔСх (Ф)

Таблица 3

ε= В, R2= Ом, С2 = Ф
Разрядка	t (с)
	U (В)
	lnU
τ2±Δτ2 (с)

Обработка результатов измерения

По результатам измерений студенты выполняют одно из следующих заданий (по указанию преподавателя).

Задание 1. Построение кривых разрядки конденсаторов и экспериментальное подтверждение закона, описывающего данный процесс.

1. Используя данные, взятые из таблиц 1 и 3, постройте графики зависимости напряжения от времени при разрядке конденсаторов С₁и С₂. Проанализируйте их, сравните с теоретическими (рис. 4).

2. Постройте графики разрядки конденсаторов С₁и С₂ в осях (lnU, t). Проанализируйте их, сравните с теоретическими (рис. 5).

3. Определите по графикам угловые коэффициенты К₁и К_2. Среднее значение углового коэффициента находится как отношение, определяющее тангенс угла наклона прямой:

.

4. Случайные погрешности графическим методом можно оценить по отклонению опытных точек относительно проведенной прямой. Относительная погрешность углового коэффициента может быть найдена согласно формуле:

,

где δ(lnU) – отклонение (в проекции на ось lnU) от прямой линии наиболее удаленной опытной точки, - интервал, на котором сделаны измерения.

5. По значениям угловых коэффициентов определите постоянные времени τ₁ и τ₂, используя формулу (9). Сравните полученные значения со значениями постоянной времени, рассчитанными по формуле (8).

6. Посчитайте относительные и абсолютные погрешности для постоянной времени: , .

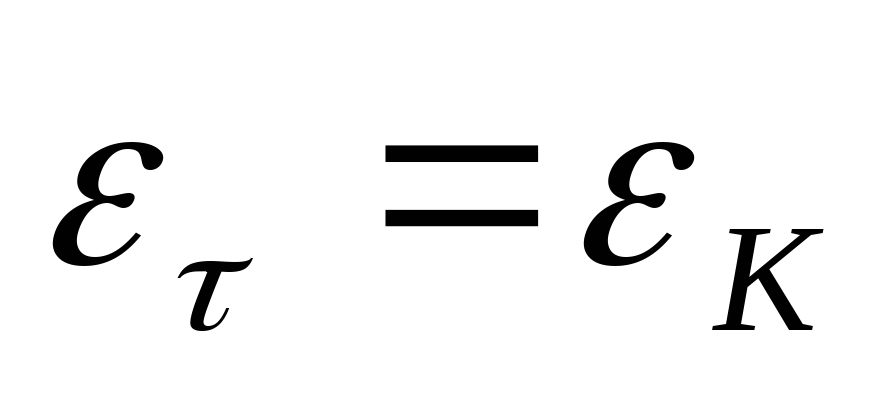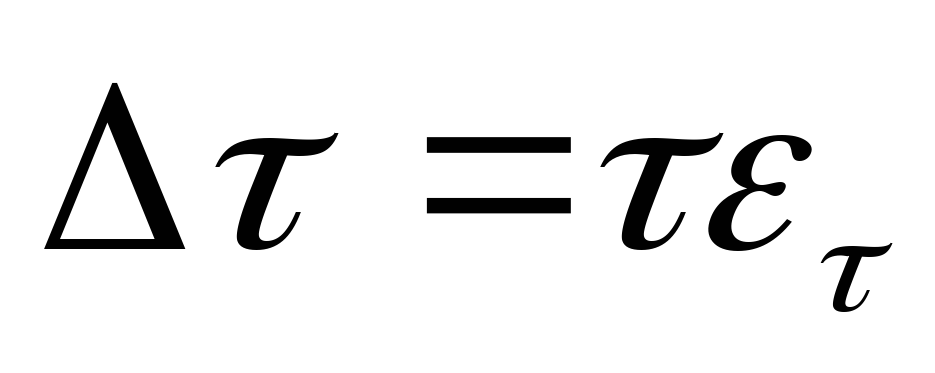7. Сделайте выводы о соответствии экспериментальных графиков экспоненциальному виду зависимости напряжения от времени, и о влиянии постоянной времени на протекание процессов зарядки и разрядки конденсатора.

Задание 2. Определение неизвестной емкости конденсатора.

1. Используя данные, взятые из таблиц 1 и 2, постройте графики зависимости напряжения от времени при разрядке конденсаторов С₁ и С_х. Проанализируйте их, сравните с теоретическими (рис. 4).

2. Постройте графики разрядки конденсаторов С₁ и С_х в осях (lnU, t). Сравните их и сделайте вывод о соотношении постоянных времени (см. рис.5).

3. Определите по формуле (10) неизвестную емкость, используя графики и данные таблиц 1 и 2.

4. Найдите относительные погрешности угловых коэффициентов ε_К1 и ε_кх (см. п.4 задания 1).

5. Определите относительную и абсолютную погрешности емкости:

, .

6. Сравните полученное значение С_х со значением, измеренным при помощи цифрового мультиметра в режиме измерения емкости. Сделайте вывод.

Дополнительное задание.

Рассчитайте энергию заряженного конденсатора, используя формулу (5).

Контрольные вопросы

1. Что представляет собой конденсатор? Что называется емкостью конденсатора?

2. Докажите, что электрическое поле плоского конденсатора сосредоточено между его обкладками.

2. Сколько надо взять конденсаторов емкостью 2мкФ и как их соединить,

чтобы получить общую емкость 5 мкФ?

3. Как можно найти энергию заряженного конденсатора?

4. Какие токи называются квазистационарными? Почему токи зарядки и разрядки конденсатора можно отнести к квазистационарным?

5. По какому закону изменяется напряжение на конденсаторе в процессах а) зарядки и б) разрядки?

6. Что показывает постоянная времени цепи? От чего она зависит?

7. Зачем в данной работе строится график зависимости lnU от t?

8. Как в данной работе определяется постоянная времени электрической цепи?

ЛИТЕРАТУРА

1.Трофимова Т.И. Курс физики. / Т.И. Трофимова. - М.: Высшая школа, 2006-2009 г. г. – 544с.

2 Савельев И.В. Курс физики. В 3-х томах. Том 2. Электричество. Колебания и волны. Волновая оптика. Изд. 3-е, стереотип. / И.В. Савельев - М.: Лань, 2007. - 480 с.

3. Грабовский Р. И. Курс физики / Р.И. Грабовский - СПб: издательство «Лань», 2012. – 608с.

4 Зисман Г. А., Тодес О. М. Курс общей физики. В 3-х томах. Том 2. Электричество и магнетизм / Г.А. Зисман, О.М. Тодес - СПб: «Лань», 2007. - 352 c.

Концевой титул

Учебное издание

Составитель:

Плотникова Ольга Васильевна