Домашнее задание 6 (второй семестр)

1. Вычислить площадь плоской фигуры, ограниченной кривой y=x²+1, осью Ox и прямыми x=1 и x=4.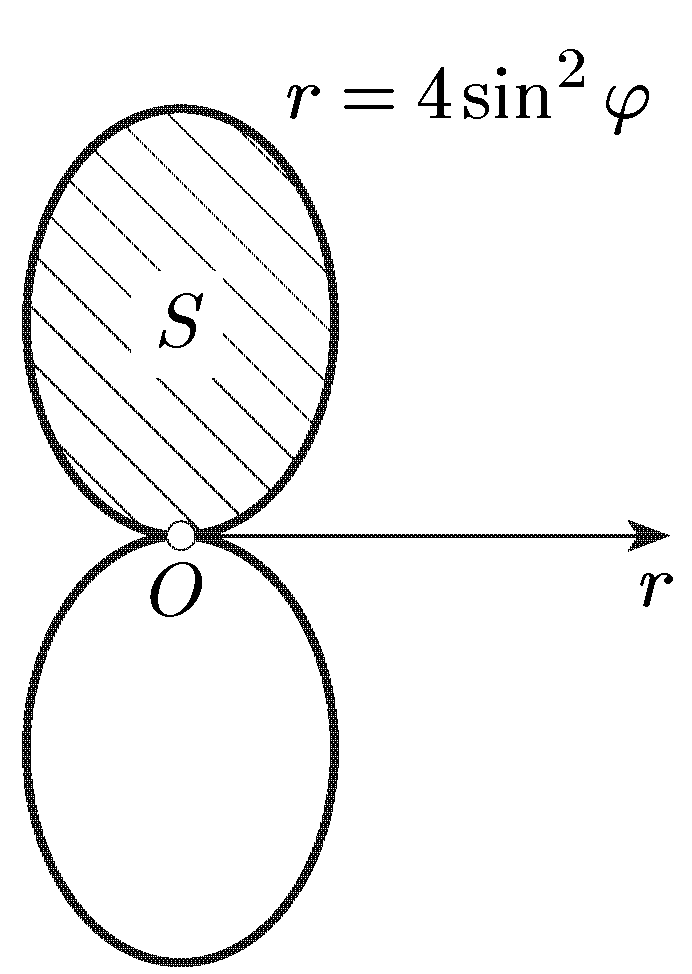

2. Найти площадь одного лепестка кривой ρ=4sin2φ (см. рис).

3. Найти площадь фигуры, ограниченной графиком функции y=sinx и осью абсцисс при условии, что 0≤x≤2π.

4. Найти объем тела, образованного вращением фигуры, ограниченной линиями xy=4; x=1; x=4; y=0 вокруг оси Ох.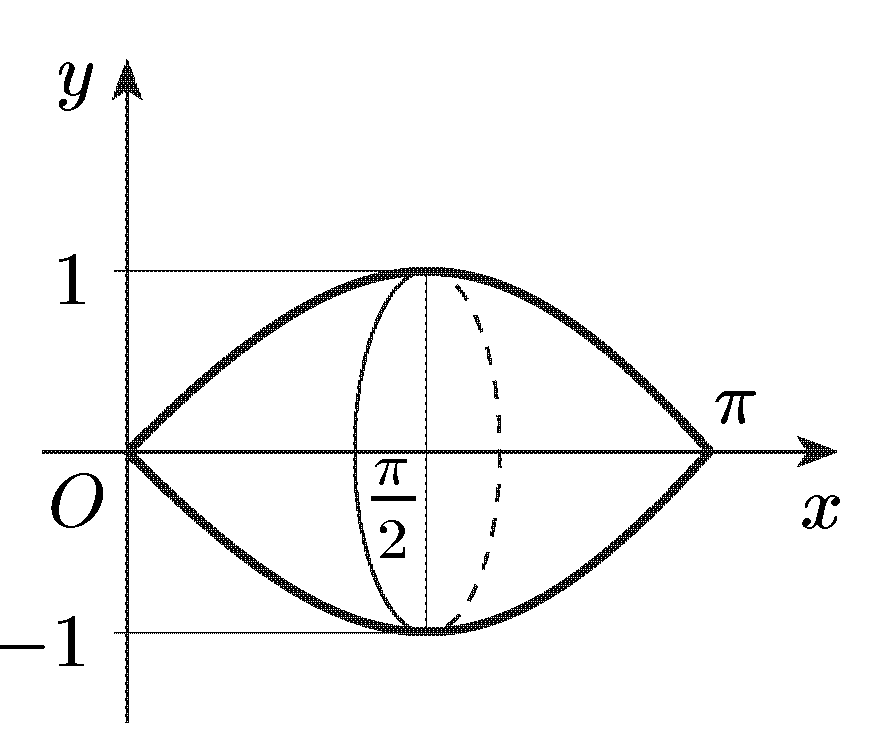

5. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной полуволной синусоиды y=sinx, 0≤x≤π и осью абсцисс (см. рис).

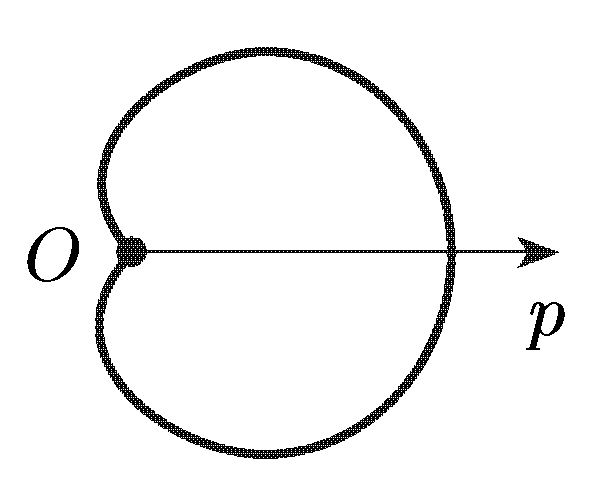
6. Вычислить длину кардиоиды 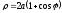(см. рис).

7. Найти длину дуги астроиды (см. рис) , расположенной в первом координатном углу.

8. Найти площадь поверхности сферического сегмента (см. рис), образованного вращением вокруг оси Ох дуги окружности 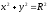, соответствующей изменению x от a до R (0<a<R).

Ответы:

1. 24 2. 3π 3. 4 4. 12π

5. π²/2 6. 16a 7. 3a/2 8. 2πR(R-a)