5.2. Представление периодических несинусоидальных величин рядами Фурье

Как известно, любая периодическая функция f(ωt), удовлетворяющая условиям Дирихле, т. е. имеющая за полный период конечное число разрывов первого рода и конечное число максимумов и минимумов, может быть представлена тригонометрическим рядом, т. е. рядом Фурье.

Токи, э. д. с. и напряжения в электрических цепях всегда удовлет­воряют условиям Дирихле. Итак, представимf(ωt) в виде тригонометри­ческого ряда:

или

(5.1)

где A₀ — постоянная составляющая или нулевая гармоника, равная сред­нему значению функции за период; A_1m sin (ωt + ψ₁) — основная сину­- соида, или первая гармоника, обладающая той же частотой, что и периоди-­ ческая несинусоидальная функция; А_2m sin (2ωt + ψ₂) — вторая гармоника, обладающая двойной частотой по сравнению с основной, называемая высшей гармоникой второго порядка; А_nm sin (nωt + ψ_n) - высшая гар­- моника n-го порядка (все члены вида А_km sin (kωt + ψ_k) при k > 1 назы-­ вают высшими гармониками); A_1m, А_2m…..А_nm — амплитуды гармоник ряда; ωt = 2π/Т— основная частота, равная частоте несинусоидальной функции; Т— период несинусоидальной периодической функции; ψ₁, ψ₂,….ψ_n — начальные фазы гармоник (за начало отсчета принимают начало периодической несинусоидальной функции). Необходимо отме­тить, что каким бы способом ни разлагали несинусоидальную периоди­ческую функцию в ряд Фурье, постоянная составляющая А₀ и амплитуды гармоник А_1m, А_2m, .... А_nm остаются неизменными. Начальные же фазы гармоник ψ₁, ψ₂,….ψ_n изменяются, если начало отсчета времени сдви­гается. При сдвиге начала отсчета соответственно изменяется также вид ряда.

В общем случае ряд Фурье содержит бесконечное число членов. На практике обычно ограничиваются некоторым их конечным числом, определяемым требуемой точностью расчета. Чаще всего ограничивают­ся той гармоникой ряда, амплитуда которой составляет менее 5% от амплитуды основной гармоники.

Для вычисления постоянной составляющей, амплитуд гармоник и их начальных фаз ряда Фурье кривой, полученной эксперименталь­ным путем, целесообразно записать ряд через синусы и косинусы без началь­ных фаз. Рассмотрим к-ю гармонику ряда:

(5.2)

где B_km = А_km cos ψ_k, С_km = А_km sin ψ_k.

Таким образом, ряд Фурье можно переписать в виде

Из (5.3) следует, что все синусоиды и косинусоиды ряда начинаются там же, где периодическая несинусоидальная функция. Однако, согласно (5.2), коэффициенты B_km и С_km зависят от выбора начала отсчета вре­мени. Коэффициенты ряда А₀, B_km и C_km определяют с помощью следую­щих интегралов:

(5.4)

(5.5)

(5.6)

Из (5.4) следует, что постоянная составляющая есть среднее зна­чение функции f(t) за период Т=2п/ω. Согласно (5.2), можно записать

(5.7)

Зная значения коэффициента ряда (5.3), можно переписать (5.1), подсчитав предварительно коэффициенты А_km по (5.7).

Любая несинусоидальная периодическая величина наряду с анали­тическим ее представлением в виде ряда Фурье может быть представ­лена в виде графика. При этом постоянную составляющую А₀ и коэф­фициенты ряда B_km и C_km определяют графическим путем: А₀ опреде­ляется как среднее значение ординаты кривой за период в n точках, а коэффициенты В_km и C_km определяют, например, путем разбивки неси­нусоидальной кривой на n равных частей (порядка двадцати) и замены интегралов (5.5) и (5.6) суммами конечного числа слагаемых. Кроме того, несинусоидальную периодическую кривую можно также разложить в ряд с помощью гармонического анализатора — прибора, применяе­мого для этой цели.

Для более наглядного представления характера изменения ампли­туд гармоник ряда от частоты kω строят диаграмму амплитудно-частот­ного спектра (рис. 5.2), а для характеристики формы кривой, зависящей в большей мере от соотношения начальных фаз гармоник ψ_к, строят диаграмму фазочастотного спектра (рис. 5.3). Так как амплитуды и начальные фазы определяют спектральный состав несинусоидальных периодических функций, который носит дискретный характер, то совокуп-

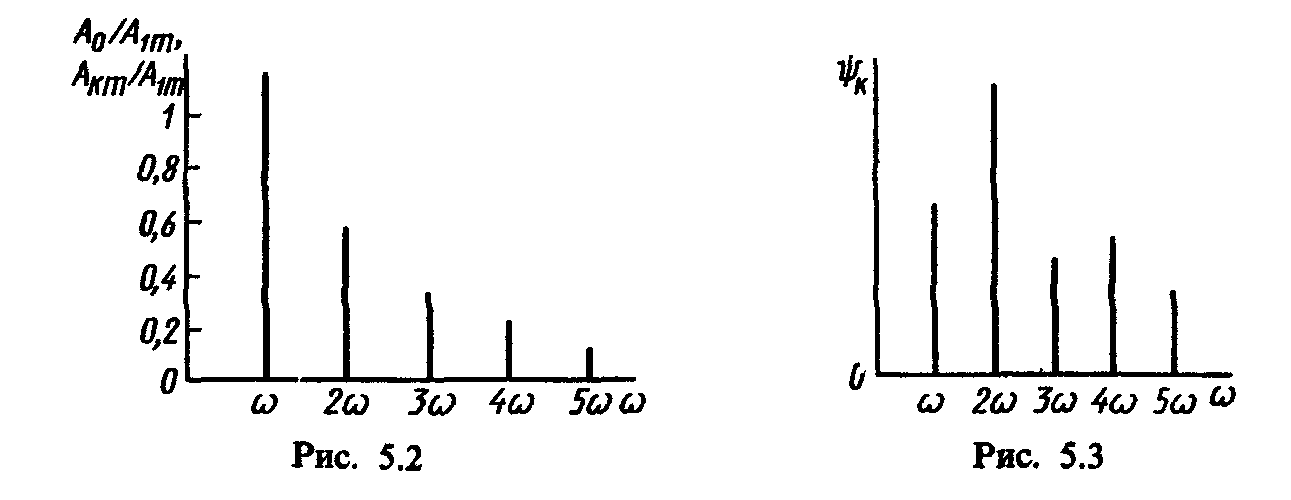
ность гармонических составляющих каждой из этих функций назыают дискретным частотным спектром.

При построении амплитудно-частотного спектра по оси абсцисс откладывают значения частот kω, а параллельно оси ординат — отно­сительные значения постоянной составляющей и амплитуд основной и высших гармоник. В диаграмме фазочастотного спектра по оси абсцисс откладывают значения частот kω, а параллельно оси ординат — от­резки, численно равные начальным фазам гармоник.