Логическое проектирование

Логические схемы выполняют логические операции над одной или несколькими логическими переменными. Логическая переменная – сигнал, принимающий значения ДА-НЕТ, ИСТИНА-ЛОЖЬ, 1-0.

Схемы, реализующие два устойчивых состояния, называются двоичными. Формальное описание двоичных схем осуществляется при помощи математического аппарата булевой алгебры. Эта алгебра оперирует булевыми переменными 0 и 1.

Основные операции булевой алгебры

- Логическое умножение, конъюнкция, «И».

Обозначение:      x.

F = A * B = A & B … и т.д.

Результат операции над логическими переменными записывается в таблицу истинности:

A	B	F
0	0	0
0	1	0
1	0	0
1	1	1

Обозначения блока, реализующего умножение в схемах:

A A

& F F

B B

- Логическое сложение, дизъюнкция, «ИЛИ».

Обозначение: .

F = A + B.

Таблица истинности:

A	B	F
0	0	0
0	1	1
1	0	1
1	1	1

Символ в схемах:

A A

F F

B B

• Инверсия, «НЕ».

Обозначения: , А, ].

F = .

Таблица истинности и обозначения:

A	F
0	1
1	0

a

a =1 f= ab +ab

bf b

Исключающее ИЛИ.

ОСНОВНЫЕ ЛОГИЧЕСКИЕ ФУНКЦИИ.

Введем понятие пропозициональная форма. Пропозициональная форма - набор символов и отношение между собой логических переменных, в простейшем варианте определения - связующая функция между переменными (объектами) в булевой логике, в которой переменные и сама функция принимают значения «0» и «1».

Основные определения булевой алгебры.

Пусть В - некоторое множество, f и g - функции, для которых при x, y, z B выполняются следующие условия

Чаще всего используют следующие функции:

а) повторение F = A, где А - переменная;

б) инверсия (отрицание, НЕ) F === A;

в) логическое сложение (дизъюнкция, ИЛИ) F = A + B = AB (функция двух переменных), выражение для большего числа переменных можно записать следующим образом F =, где- переменные;

г) логическое умножение (конъюнкция, И) F = A * B = A & B = AB (функция двух переменных), выражение для любого числа переменных - F =, где- переменные;

д) операция ИЛИ-НЕ F = (A + B) = ( стрелка Пирса); соответственно для нескольких переменных F =

е) операция И-НЕ F = (штрих Шеффера), для нескольких переменных -

F = переменные;

ж) операция «эквивалентность» F = AB = (A  B) , функция принимает истинностные значения при равенстве значений А и В;

з) операция «неэквивалентность» F = A  B , функция принимает истинностные значения при неравенстве значений А и В («исключающее ИЛИ»);

и) операция «импликация» F = A  B , значение «ложно» функция принимает лишь при условии, когда А истинно, а В - ложно, то есть А  В = А &( В).

Следствие: если А и В пропозициональные формы (логические выражения), то и любые логические выражения с этими пропозициональными формами также являются логическими выражениями.

Любая пропозициональная форма может быть определена 3-мя связками: , &,  (НЕ, И, ИЛИ = инверсия, конъюнкция, дизъюнкция).

Любую функцию можно представить в нормальной конъюнктивной или нормальной дизъюнктивной форме, как сумму произведений либо произведение сумм прямых и инверсных значений переменных.

РАСПРОСТРАНЕННЫЕ АЛГЕБРАИЧЕСКИЕ ТОЖДЕСТВА

1. x + x = x * j * x * x = x - идемпотентность;

2. (x + y) + z = x + (y + z) - ассоциативность;

3. (x * y) = (y * x), (x + y) = (y + x) - коммутативность;

4. x (x + y) = x * y + x = x - поглощение;

5. (x + y) * z = x * z + y * z -дистрибутивность;

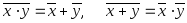6. - правила Де-Моргана.

УСЛОВНО-ГРАФИЧЕСКИЕ ОБОЗНАЧЕНИЯ .

Приведем примеры обозначений логических элементов, наиболее часто применяемых в схемотехнике.

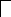А F=

Повторитель А F ; инвертор А о F =; инвертор- > o

усилитель

А 0 F =

A A x_o

B & F=A*B B &⁰ F = &

И И-НЕ x_n-1 И для многих перемен

А А х₀

1 F=A+B 1 F=1 F=

В В ^{0 0}

х_n-1

ИЛИ ИЛИ-НЕ ИЛИ-НЕ для многих переменных

х1 х1

 = 1

F =F

x2 x2

Исключающее ИЛИ, неэквивалентность.

Символ ^О - означает инверсию на выходе. В любой элемент может быть добавлен символ > , означающий усиление сигнала на выходе.

Пример. Приведем пример представления логической функции в пропозициональной форме и ее структурную схему.

Пусть известна таблица истинности для некоторой функции, которую нужно реализовать схемотехнически.

x1	x2	x3	F
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	1
1	1	1	0

F=P₁+P₂+P₃.

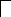x1

^x o P₁

&

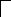
^x P₂ 1 F

x2 &

^{x O}

& P₃

_O

x3

Основные логические функции можно проиллюстрировать примерами пересечения множеств:

«И» = & «ИЛИ» =  = +

А А

В В

«И-НЕ» =  (А&B) = A B «ИЛИ-НЕ» =  (А В) = А  В

В ВВВ В В

А А А

инверсия «НЕ» =  «импликация» = А&( В)

А А А В

Приведем примеры схемной реализации ряда распространенных логических функций с использованием трех основных логических действий (, , ):

« импликация» F =     *, таблица истинности функции:

A &

A	B	F
0	0	0
0	1	0
1	0	1
1	1	0

B _{O O} f =(АВ)=

«тавтология» F = А =1, А

&

О О 1

при помощи последней схемы можно выполнить

схему формирования сигнала, введя линию задержки из нечетного числа инверторов:

А

& o

Л.З. о

«Бистабильная ячейка» F =

A F