Шпоры / Шпоры(insomnia&co_edition) / 16+18+

16.Зонная диаграмма равновесного p-n-перехода. Условия равновесия. Контактная разность потенциалов p-nерехода.

В состоянии равно­весия, когда к переходу не приложено внешнее напряжение, через не­го протекают одновременно четыре различных тока. Запишем их, поль­зуясь величиной плотности тока j , т.е. тока, протекающего через единичное поперечное сечение: диффузионный

ток дырок, обуслов­ленный их движением из области р в область п ; - диффузионный ток электронов, связанный с движением электронов из области n в область р .

Обе эти составляющие связаны с движением основных носителей под действием диффузии. Если бы не было ограничивающего фактора, диффузионные движения носителей продолжались бы до тех пор, пока концентрация электронов и дырок в обеих областях не выровнялась бы и мы бы уже не смогли различить ни р -, ни п -области. Таким ограничивающим фактором является внутреннее электрическое поле, возникающее в области перехода и ограничивающее диффузионные потоки носителей через переход. Образование этого поля связано с тем, что носители, диффундируя в соседнюю область (электроны – в р-область, дырки - в п -область), оставляют после себя неподвижные копы доноров и акцепторов. В результате п-область становится заряженной поло­жительно, р-область - отрицательно, и возникают два слоя объем­ных зарядов, между которыми существует внутреннее электрическое поле, характеризующееся напряженностью (рис.2.2). Преодо­леть тормозящее действие этого поля и проникнуть в соседнюю об­ласть совершающие диффузионное движение носители могут только в том случае, если они обладают достаточно большой энергией. В то же время внутреннее электрическое поле подхватывает в каждой области неосновные носители, которые, совершая тепловое движение, попада­ют на границы областей объемных зарядов, и переносят их в сосед­нюю область. Поэтому к указанным диффузионным токам, протекающим через переход, добавятся еще два: - дрейфовый ток дырок из области п в область p; - дрейфовый ток электронов из области р в область п .

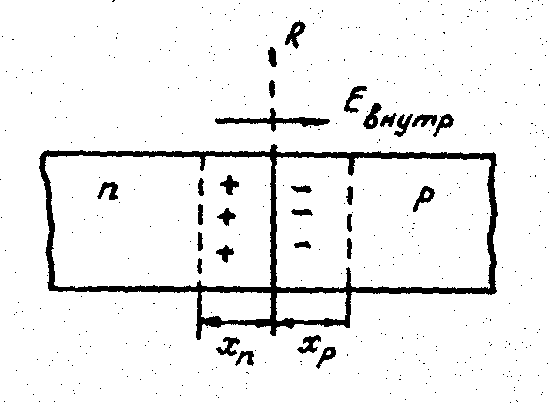
Рис.2.2. Образование областей объемных зарядов в р- п -переходе.

В состоянии равновесия сумма всех четырех указанных токов в р -п-переходе равна нулю: или полный ток через переход

вопросик !6б

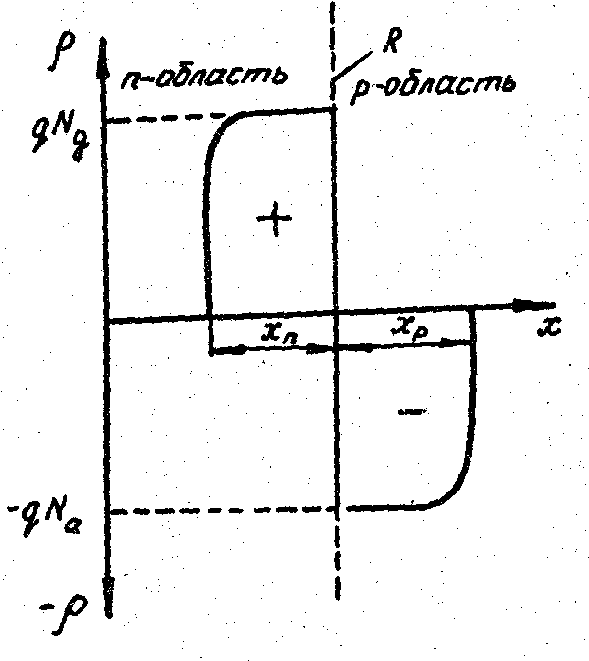
Рис. 2.3. Распределение плотности объемного заяда вдоль перехода.

На рис.2.3 показано распределение плотности объемного заряда р в области р-п-перехода, х_п и х_р - границы областей объемных зарядов в п- и р-областях. Так как концентрации подвижных носите­лей заряда в области перехода понижены, то их при расчетах обычно не учитывают. Заряды в обеих областях равны по величине и противо­положны по знаку. За пределами областей, при х< х_п и х>х_p концентрации свободных носителей заряда становятся соизмеримыми c концентрациеями йонов примеси, и , поэтому здесь можно считать .

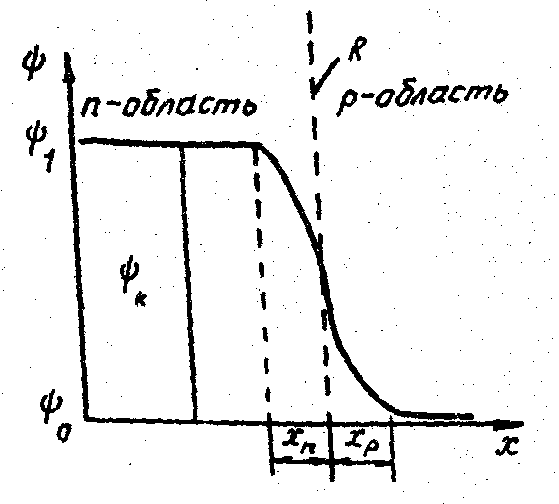
Рис.2.4. Распределение потенциала вдоль перехода.

На рис. 2.4 приведен график изменения потенциала в области p-n-перехода. Максимальная скорость изменения потенциала соответствует плоскости раздела областей p- и n-типа проводимости. За пределами областей положительного и отрицательного объемных зарядов будут потенциальные значения потенциалов в n-области и в p-области. Таким образом, иежду областями p- и

n-типа существует контактная разность потенциалов .

Поскольку напряженность электрического поля Е связана с потен­циалом, то в одномерном случае, когда изменение происходит только вдоль координаты х,

,

можно построить зависимость Ё(х) в области перехода, которая показана на рис.2.5.

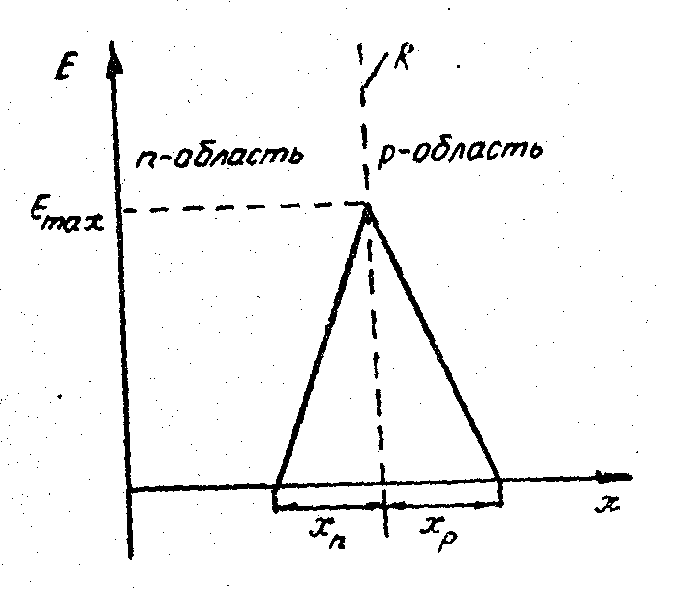
Рис.2.5. Распределение напря­женности электрического поля вдоль перехода

Максимальное значение напряженности электри­ческого поля соответствует плоскости раздела R . Как уже говори­лось, внутреннее электрическое поле обусловлено наличием в об­ласти перехода объемных зарядов, а за его пределами при х< х_n и х>x_p р=0 и E=0. Значение Е_тах может быть определено из уравнения Пуассона:

(2.3)

18.Барьерная ёмкость p-n-перехода

При подаче на p-n-переход переменного напряжения проявляются емкостные свойства.

Образование p-n-перехода связано с возникновением пространственного заряда, создаваемого неподвижными ионами атомов доноров и акцепторов. Приложенное к p-n-переходу внешнее напряжение изменяет величину пространственного заряда в переходе. Следовательно, p-n переход ведет себя как своеобразный плоский конденсатор, обкладками которого служат области n- и p-типа вне перехода, а изолятором является область пространственного заряда, обедненная носителями заряда и имеющая большое сопротивление.

Такая емкость p-n-перехода называется барьерной. Барьерная емкость C_Б может быть рассчитана по формуле

,

где

S - площадь p-n-перехода;  ·₀ - относительная () и абсолютная (₀) диэлектрические проницаемости;  - ширина p-n-перехода.

Особенностью барьерной емкости является ее зависимость от внешнего приложенного напряжения. С учетом (2.2) барьерная емкость для резкого перехода рассчитывается по формуле:

,

г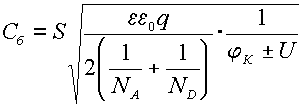де знак ” + “ соответствует обратному , а ”-“ прямому напряжению на переходе.

Зависимость барьерной емкости от обратного напряжения называется вольтфарадной характеристикой (см. рис. 2.6). В зависимости от площади перехода, концентрации легирующей примеси и обратного напряжения барьерная емкость может принимать значения от единиц до сотен пикофарад. Барьерная емкость проявляется при обратном напряжении; при прямом напряжении она шунтируется малым сопротивлением r_pn .

Кроме барьерной емкости p-n-переход обладает так называемой диффузионной емкостью. Диффузионная емкость связана с процессами накопления и рассасывания неравновесного заряда в базе и характеризует инерционность движения неравновесных зарядов в области базы.

Диффузионная емкость может быть рассчитана следующим образом:,

Вопрос 18б

г

. Суммарная

емкость p-n-перехода определяется суммой барьерной и диффузионной емкостей. При обратном напряжении C_Б > C_ДИФ; при прямом напряжении преобладает диффузионная емкость C_ДИФ >> C_Б.Эквивалентная схема p-n-перехода на переменном токе представлена на рис. 2.7. На эквивалентной схеме параллельно дифференциальному сопротивлению p-n-перехода r_pn включены две емкости C_Б и C_ДИФ ; последовательно с r_pn включено объемное сопротивление базы r_Б. С ростом частоты переменного напряжения, поданного на p-n-переход, емкостные свойства проявляются все сильнее, r_pn шунтируется емкостным сопротивлением и общее сопротивление p-n-перехода определяется объемным сопротивлением базы. Таким образом, на высоких частотах p-n-переход теряет свои нелинейные свойства.

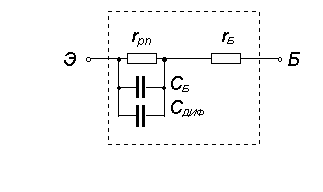Рис.27

вопросик !6в

где -относительная диэлектрическая проницаемость полупроводникового материала; - диэлектрическая проницаемость вакуума

(2.4)

х_n и x_p - границы областей объемных зарядов.

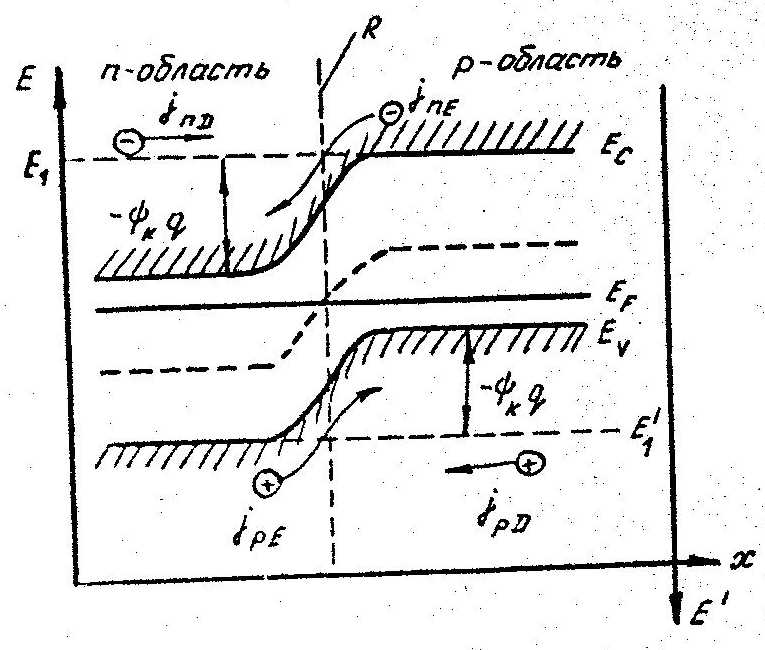
Рис.2.6. Энергетическая диаграмма p-n-перехода.(По оси ординат отложены энергия E для электрона, которая увели­чивается снизу вверх, и энергия для дырки, которая . увеличивается

сверху вниз).

На рис.2.6 представлена энергетическая диаграмма p-n-перехода. На границе раздела, в плоскости R, уровень Ферми проходит через середину запрещенной зоны, что соответствует случаю собственного полупроводника.

Диффузионный переход из области n в область p совершают электроны, имеющие энергии , а из области p в область n – дырки с энергией . Дрейфовое движение осуществляется носителями, которые можно представить, прибегая к аналогии, скатывающимися с горки. При этом «скатываются» из области n в область p, а электроны – из области p в область n.

Высота потенциального барьера

схематически показана на рис.2.6.

Контактная разность потенциалов может быть выражена как

и будет тем выше, чем больше концентрации основных носителей в обеих областях. При увеличении концентрации основных носителей (степени легирования) уровень Ферми в n-областях стремится к , в p-области – к E_V и высота потенциального барьера на границе p-n-перехода стремится к ширине запрещенной зоны полупроводника.