2. Обеднение и слабая инверсия в примесном полупроводнике

Для этой области, как следует из (3.15), функция F(ψ, φ₀) имеет совсем простой вид. Второй интеграл уравнения Пуассона при этом будет равен:

. (3.48)

Используя граничное условие, что при z = W, т.е. ширине ОПЗ в обеднении и слабой инверсии потенциалаψ = 0, получаем непосредственным интегрированием:

. (3.49)

Таким образом, из (3.49) следует, что потенциал ψв ОПЗ в случае обеднения и слабой инверсии квадратично спадает по глубине ОПЗ. Поскольку толщина инверсионного слоя много меньше ширины обедненной области, то в первом приближении

. (3.50)

Потенциал ψв области слабой инверсии спадает по толщине инверсионного слоя по линейному закону, поэтому говорят о треугольной потенциальной яме на поверхности.

3. Область обогащения и очень сильной инверсии в примесном полупроводнике

Будем рассматривать область изменения поверхностного потенциала ψ_s, когда для зарядов в ОПЗ справедливы соотношения (3.19) и (3.22). Получим форму потенциального барьераψ(z) для случая инверсии, а для случая обогащения вид будет аналогичный.

Из (3.44) и (3.15) следует, что при βψ > 7

. (3.51)

Непосредственное интегрирование (3.51) приводит к зависимости:

. (3.52)

Для случая обогащения аналогично получаем:

. (3.53)

Потенциал ψ(z) в этой области меняется по логарифмическому закону, в таком случае говорят о логарифмической яме на поверхности полупроводника.

3.3. Емкость области пространственного заряда

Поскольку полный заряд в ОПЗ Q_scзависит от величины поверхностного потенциалаψ_s, то область пространственного заряда обладает определенной емкостьюC_sc.

Величина C_sc, как следует из соотношения (3.18), будет равна:

. (3.54)

Для того, чтобы получить выражения для емкости ОПЗ в различных случаях (обеднение, обогащение, инверсия), можно либо непосредственно воспользоваться (3.54), либо воспользоваться выражениями для заряда Q_sc, полученными в разделе 3.2.2. Напомним, что рассматривается полупроводникp-типа.

Область обогащения (ψ_s < 0)

Емкость ОПЗ C_scобусловлена емкостью свободных дырокC_p:

. (3.55)

Область обеднения и слабой инверсии (2φ₀ > ψ_s > 0)

Емкость ОПЗ C_scобусловлена емкостью области ионизованных акцепторовC_B:

. (3.56)

Из соотношения (3.56) следует, что емкость C_scв области обеднения слабо зависит от поверхностного потенциалаψ_s, убывая с ростом последнего. Минимальное значение емкостиC_scдостигается вблизи порогового значения поверхностного потенциала.

Емкость ОПЗ в области обеднения и слабой инверсии эквивалентна емкости плоского конденсатора, заполненного диэлектриком с относительной диэлектрической проницаемостью ε_s, пластины которого находятся друг от друга на расстоянииW, равном ширине ОПЗ.

Плоские зоны (ψ_s = 0)

Соотношения (3.55) и (3.56) несправедливы при ψ_s → 0, т.е. в области плоских зон у поверхности полупроводника. Непосредственная подстановкаψ_s = 0 в выражение (3.55) приводит к неопределенности типа «ноль делить на ноль».

Для расчета емкости плоских зон C_FBнеобходимо провести разложение экспоненты в (3.55) в ряд и после предельных переходов имеем:

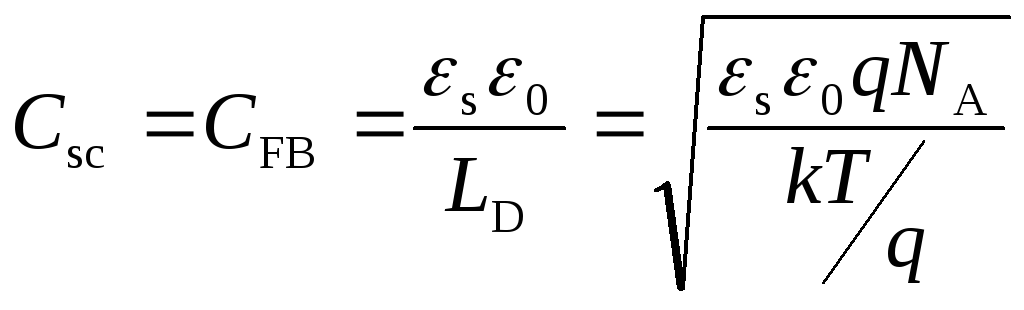. (3.57)

Емкость ОПЗ в плоских зонах эквивалентна емкости плоского конденсатора с обкладками, удаленными на дебаевскую длину экранирования.

Область сильной инверсии (ψ_s > 2φ₀)

Емкость ОПЗ C_scобусловлена емкостью свободных электроновC_nв инверсионном слое и при достаточно больших значениях поверхностного потенциалабудет равна:

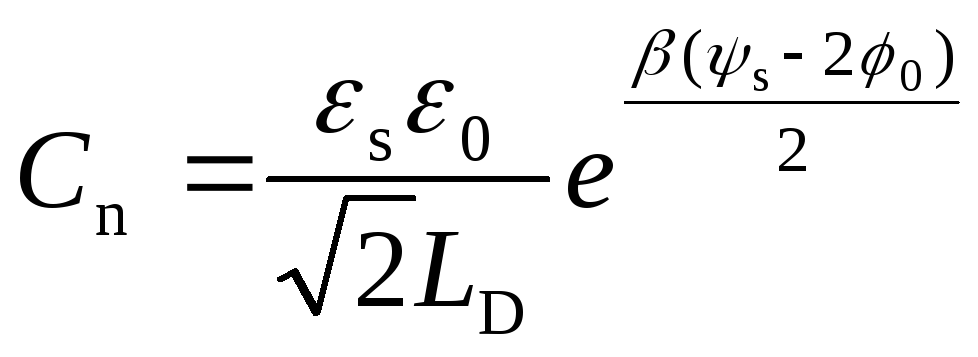. (3.58)

Из анализа (3.55) и (3.58) следует, что емкости свободных носителей в обогащении и сильной инверсии экспоненциально зависят от поверхностного потенциала ψ_sи имеют одинаковые значения, если величину поверхностного потенциала отсчитывать для инверсии от порогового значенияψ_s = 2φ₀.

На рисунке 3.7 приведен график зависимости емкости ОПЗ C_scот величины поверхностного потенциалаψ_s, рассчитанной по соотношениям (3.55 – 3.58).

Рис. 3.7. Зависимость емкости области пространственного заряда C_scот поверхностного потенциала, рассчитанная в классическом (сплошная линия) и вырожденном (пунктирная линия) случае