2.5. Метод сильносвязанных электронов

Решение уравнения Шредингера в этом методе производится с помощью теории возмущений квантовой механики. Предполагается, что электроны сильно связаны с ионами и их движение в кристалле мало отличается от движения внутри изолированного атома. В качестве нулевого приближения используются волновая функция Ψa и энергия Ea электрона в изолированном атоме, которые считаются известными. За малое возмущение этого внутриатомного движения электронов принимается взаимодействие с соседними атомами. При этом предполагается, что волновые функции электронов соседних атомов перекрываются незначительно, а для более далеких атомов это перекрытие практически отсутствует. В результате перекрытия волновая функция каждого электрона изменяется, и ее ищут в виде линейной комбинации атомных волновых функций:

Ψ(r )= ∑CnΨan , n

где Ψan - атомная волновая функция электрона, локализованного вблизи n-го атома.

Для одномерного кристалла с параметром решетки a приближение сильносвязанных электронов приводит к следующему выражению для энергетического спектра электронов:

где Ea - невырожденный энергетический уровень электрона в изолированном атоме; C - средняя энергия электрона в кристалле; A - обменный интеграл, определяемый величиной перекрытия волновых функций электронов n-го и (n + 1)-го атомов:

В выражение для обменного интеграла входит величина возмущения w =U (r )−Ua (r ), равная разности энергий электрона в кристалле и

в изолированном атоме.

28

Из выражения (2.5) следует, что дискретный атомный уровень Еа при образовании кристалла опускается на величину С, поскольку средняя энергия электрона в кристалле отрицательна, и расщепляется в энергетическую зону (рис.2.5). Внутри зоны энергия периодически зависит от вектора к.

Ea

Рис.2.5. Расщепление атомного энергетического уровня Ea в энергетическую зону при образовании кристалла

Расщеплению подвергаются все атомные уровни, поэтому энергетический спектр электрона в кристалле представляет собой чередование

29

Знак обменного интеграла определяется знаком волновых

ния w, который всегда отрицателен. Для s и d атомных волновых функций A < 0, а для p функций A > 0.

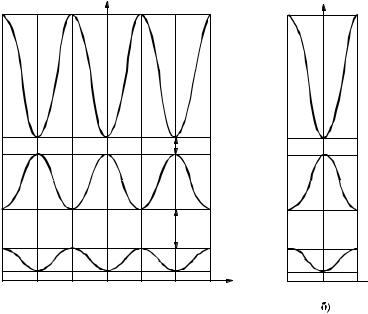
Схематически закон дисперсии для энергетических зон, образовавшихся от расщепления s, p и d атомных уровней, представлен на рис.2.7,а. Предполагается, что в общем случае энергетические зоны, полученные от расщепления соседних уровней, не перекры-

Рис.2.7. Закон дисперсии для энергетических зон, образовавшихся от

ваются. Перекрытие зон будет рассмотрено позднее. В связи с периодичностью функции Е(к) энергетический спектр электрона в кристалле достаточно рассмотреть в пределах 1-й зоны Бриллюэна.

В этом случае говорят о картине приведенных энергетических зон

(рис.2.7,б).

Проведенный анализ относился к расщеплению невырожденных энергетических уровней. Расчеты показывают, что вырожден-

30

2.6. Металлы, диэлектрики и полупроводники с точки зрения зонной теории

Представление о разрешенных и запрещенных энергетических зонах позволяет объяснить различие свойств металлов, диэлектриков и полупроводников. Проведем эту классификацию, исходя из структуры энергетических зон кристаллов и заполнения их элек-

тронами.

При образовании кристалла расщепляются все атомные энергетические уровни - и содержащие электроны, и возбужденные уровни, на которых нет электронов. Если атомный уровень невырожден, то в энергетической зоне, полученной от его расщепления, содержится N уровней, на каждом из которых могут находиться два электрона с противоположными спинами. Таким образом, общее число квантовых состояний в зоне равно 2N.

Если энергетический уровень g-кратно вырожден, то он расщепляется на g подзон, каждая из которых содержит 2N состояний, т.е. всего образуется 2Ng состояний.

При перекрытии зон число состояний в них суммируется. Заполнение образовавшихся энергетических зон электронами при

Т = 0 происходит таким образом, чтобы энергия системы была минимальна, поэтому электроны заполняют прежде всего низкорасположенные зоны. Если зона образовалась от расщепления невырожденного и полностью заполненного уровня, то и она оказывается полностью заполненной. В этом случае 2N электронов полностью заполняют 2N состояний в зоне. Если на исходном атомном уровне находился один электрон, то и образовавшаяся зона будет заполнена лишь наполовину.

Аналогичная ситуация возникает и при заполнении подзон, порожденных расщеплением вырожденного уровня. Если этот уровень заполнен полностью, то будут заполнены и все подзоны. Если вырожденный уровень заполнен неполностью, то некоторые подзоны могут оказаться частично заполненными или пустыми.

Образование неполностью заполненных зон может быть обусловлено также перекрытием пустых и полностью заполненных зон и подзон, образовавшихся от расщепления разных атомных уровней.

Самая верхняя разрешенная зона, в которой при T = 0 имеются заполненные энергетические уровни, называется валентной зоной. Она образуется или при расщеплении валентного уровня атома, или при на-

32

ложении зон, в котором принимает участие хотя бы одна подзона, полученная от расщепления валентного уровня. Потолок валентной зоны обозначается через Ev.

Энергетическая зона, расположенная выше валентной и отделенная от нее запрещенной зоной, называется зоной проводимости. Ее дно обозначается через Eс. При T = 0 зона проводимости пуста, электронов в ней нет.

Электроны полностью и частично заполненных зон по-разному реагируют на приложение электрического поля. В электрическом поле электроны ускоряются и увеличивают свою энергию. На энергетической диаграмме это соответствует переходу на более высокие энергетические уровни. Будем предполагать, что электрическое поле слабое и электроны могут переходить только на близлежащие энергетические уровни внутри зоны. Однако в полностью заполненной зоне все состояния заняты, и такие переходы запрещены принципом Паули. Следовательно, электроны полностью заполненной зоны не могут участвовать в электропроводности. Для того чтобы возникал электрический ток, должна иметься хотя бы одна неполностью заполненная зона.

Твердые тела, валентная зона которых при Т = 0 заполнена неполностью, называются металлами. Например, у щелочных металлов Li, Na, K на валентном s-уровне находится один электрон. При расщеплении этого уровня образуется наполовину заполненная валентная зона

(рис.2.10).

У щелочноземельных металлов Be, Mg, Ca неполностью заполненная валентная зона возникает в результате перекрытия полностью за-

(рис.2.11).

34

Если при Т = 0 валентная зона заполнена полностью, а зона проводимости, отделенная от нее запрещенной зоной, пуста, то такие кристаллы являются либо диэлектриками, либо полупроводниками (рис.2.12). При Т = 0 данные кристаллы не могут про-

называют собственной проводи- полупро-водников и диэлектри-

мостью. При данной температуре ее величина определяется ши-

риной запрещенной зоны. Данный факт лежит в основе формального деления твердых тел на диэлектрики и полупроводники. Обычно к диэлектрикам относят твердые тела, у которых Eg > 3 эВ, а к полупроводникам те, у которых Eg < 3 эВ.

Однако такое деление не учитывает важной особенности полупроводников, отличающих их от диэлектриков. Она заключается в сильной зависимости проводимости полупроводников от наличия примесей. Например, добавление в чистый кремний атомов бора в соотношении один атом бора на 105 атомов кремния увеличивает проводимость кремния при комнатной температуре в тысячу раз по сравнению с собственной. В то же время примеси мало влияют на проводимость диэлектриков.

В указанную классификацию хорошо укладываются важнейшие полупроводники Ge (Eg = 0,72 эВ), Si (Eg = 1,21 эВ) и GaAs (Eg = 1,43 эВ). В то же время кристаллы алмаза (углерод)

С (Eg = 5,48 эВ), AlN (Eg = 6,28 эВ), ZnS (Eg = 3,84 эВ) и многих других веществ также являются полупроводниками, хотя ширина их запрещенной зоны превышает 3 эВ.

35