al09

23

Так как P > 0 , то и P−1 > 0 , тогда

e= fP−1

иe Î E + (f ), т.е. E + (e)Í E + (f ) или E + (f )= E + (e).

Определение 9.8. Вещественное линейное пространство L n на-

зывается ориентированным, если из двух классов базисов указан один. Базисы выбранного класса называются положительно ори- ентированными.

9.7. Линейное подпространство

Определение 9.9. Подмножество P линейного пространства L будем называть его подпространством, если каждая линейная

комбинация

образует наименьшее возможное нулевое подпространство P = {q} и само множество L n является максимально возможным подпро- странством пространства L n . Эти подпространства мы будем

называть тривиальными подпространствами.

2. Рассмотрим однородную систему линейных уравнений с n неизвестными. Совокупность всех решений этой системы есть подпространство в линейном пространстве столбцов высоты n .

Каждая фундаментальная система решений данной однородной

24

системы есть базис в этом подпространстве. Если ранг системы ра- вен r < n , то фундаментальная матрица состоит из n − r линейно не- зависимых столбцов высоты n и мы имеем подпространство размер- ности n − r .

3. В пространстве L3 все векторы, параллельные какой-либо плоскости или прямой, образуют соответственно подпростран- ства L 2 или L1 .

9.8. Линейная оболочка

Важным способом построения линейных подпространств является образование линейной оболочки заданной системы век- торов.

Пусть дано некоторое множество P векторов в линейном про- странстве L n . Пусть L ′ - совокупность всевозможных линейных комбинаций, каждая из которых составлена из конечного числа век- торов из P . Очевидно, что L ′ есть подпространство в L n .

Действительно, если векторы x, y L ′ , то их можно предста-

вить в виде конечных линейных комбинаций x = λ1 p1 + λ2 p2 + ... + λk pk , y = μ1q1 + μ2q2 + ... + μmqm ,

Построенное таким образом подпространство L ′ называет-

ся линейной оболочкой множества P .

26

Предложение 9.15. Пусть L k′ - подпространство в L n . Если базис e1,e2 ,...,ek в L k′ дополнить до базиса e1,e2 ,...,ek ,ek +1,...,en в L n , то в таком базисе все векторы из L k′ и только они будут иметь компо-

ненты

ξk +1 = ξk +2 = ... = ξn = 0 .

Действительно, если для вектора x имеем

ξk +1 = ξk +2 = ... = ξn = 0 ,

тогда

x= ξ1e1 + ξ2e2 +... + ξk ek

итаким образом x L k′ .

Обратно, пусть вектор x L k′ раскладывается в линейную

комбинацию

(9.28) можно рассматривать как систему из n − k линейных урав- нений, связывающих координаты вектора x . Ранг такой системы равен n − k .

Предложение 9.16. Пусть в L n выбран базис. Тогда координат- ные столбцы векторов, принадлежащих k -мерному подпростран- ству L k′ (k < n), удовлетворяют однородной системе линейных уравнений ранга n − k .

ти систему линейных уравнений, определяющих линейную обо-

27

r . Для того, чтобы элемент p(t)= x1 + x2t + x3t 2 + x4t3 принадлежал L′ необходимо и достаточно, чтобы ранг расширенной матрицы (A x) тоже был равен r . Если теперь с помощью элементарных

преобразований привести матрицу (A x) к ступенчатому виду то в последних n − r строках появятся равные нулю линейные комбина- ции чисел x1,...,x4 , которые и дадут нам искомую систему уравне- ний. Итак

Так как ранг матрицы A равен 2, тогда для того чтобы ранг расширенной матрицы (A x) тоже был равен 2 необходимо и

достаточно выполнение условий x1 - x2 + x3 = 0 ,

x1 - x4 = 0 .

Это и есть искомая система линейных уравнений, определяющая линейную оболочку L′ векторов p1 (t) и p2 (t) в базисе 1,t,t2 ,t3 .

9.9.Сумма и пересечение подпространств

Пусть L ′ и L ′′ - подпространства пространства L n . Определение 9.10. Суммой подпространств L ′ + L ′′ будем назы- вать линейную оболочку их объединения L ′ U L ′′ .

Это означает, что вектор x L ′ + L ′′ , и только он, может быть

представлен в виде

e1,e2 ,...,ek ,f1,f2,...,fl . Векторы, координатные столбцы которых

будут базисными столбцами полученной матрицы и составят ба- зис в L ′ + L ′′ .

Определение 9.11. Под пересечением L ′ I L ′′ подпространств L ′ и L ′′ будем понимать множество векторов, которые принадлежат обеим подпространствам.

Очевидно, что L ′ I L ′′ есть подпространство. Это следует из того, что нулевой вектор θ лежит как в L ′ , так и в L ′′ , а значит и в L ′ I L ′′ . Далее, если векторы x, y L ′ I L ′′ , то они лежат как в L ′ , так и в L ′′ . Тогда их сумма x + y и при любом α вектор αx

29

лежат как в L ′ , так и в L ′′ , а значит и в L ¢ I L ¢¢ .

Нам известно, что в конечномерном пространстве подпрос- транства могут быть заданы системами линейных уравнений. Тогда их пересечение задаётся системой уравнений, полученной объединением систем, задающих подпространства.

Если число подпространств L1,L2 ,...,Ls , то их сум-

ма и пересечение будут определяться аналогично, с соблюдени- ем полученных ранее свойств.

В частности суммой подпространств L1,L2 ,...,Ls будет назы-

ваться линейная оболочка их объединения, т.е. множество векто-

А так как векторы всех базисов в совокупности могут быть линейно зависимыми, размерность суммы подпространств может оказаться меньше общего числа векторов в системе:

dim(L1 + L2 + ... + Ls )£ dim L1 + dim L2 + ... + dim Ls . (9.31)

s

Определение 9.12. Сумма подпространств åLi называется пря-

i=1

мой суммой если её размерность равна сумме размерностей её со- ставляющих подпространств, т.е. в (9.31) имеет место знак ра- венства.

Прямую сумму подпространств обозначают символом Å , например L = L ¢ Å L ¢¢ .

Предложение 9.17. Для того, чтобы сумма L ′ подпространств L1,L2 ,...,Ls была прямой суммой

30

L = L1 Å L2 Å... Å Ls ,

необходимо и достаточно выполнение любого из следующих условий:

зис в L ′ .

Покажем, что из определения прямой суммы следует свой- ство 1, и каждое последующее свойство (2, 3, 4) следует из преды- дущего. Так как из свойства 4 следует само определение прямой суммы подпространств, это будет обозначать равносильность каждого из свойств определению прямой суммы подпространств.

1. Докажем от противного, что из определения следует свой- ство 1. Допустим, что нашлась линейно зависимая система нену-

левых векторов

таких, что никакие два из них не лежат в одном и том же подпро- странстве Li . Дополним каждый из этих векторов до базиса в его подпространстве, а в тех подпространствах, из которых в систе- ме (9.32) представителей нет, выберем базис произвольно.

Объединением этих базисов будет система из

k = dim L1 + dim L2 + ... + dim Ls

векторов. Каждый вектор из L ′ раскладывается по этой системе, но система эта линейно зависима, так как содержит линейно зави- симую подсистему (9.32). В силу этого базис в L ′ содержит мень- ше, чем k векторов, и размерность суммы меньше суммы раз- мерностей.

2. Покажем, что из 1 → 2 . Допустим, что 2 не выполнено и

31

некоторый вектор x представлен как сумма

x = x1 + x 2 + ... + x s

и как сумма

x = y1 + y2 + ... + ys ,

где xi , yi Î Li , (i = 1...s).

Тогда

x - x = (x1 - y1 )+ (x 2 - y2 )+ ... + (x s - ys )= q .

Если хоть одна из разностей xi - yi ¹ q , мы получаем проти- воречие со свойством 1.

3. Докажем от противного, что из 2 → 3 . Допустим (для оп-

Каждый вектор из L ′ обязательно раскладывается по этой систе- ме и нам надо показать, что при выполнении условия 3 эта систе- ма линейно независима.

Будем рассуждать от противного. Допустим, что существу-

ет равная нулевому вектору нетривиальная линейная комбинация всех векторов, входящих в рассматриваемые базисы подпрост-

ранств Li (i = 1...s). Группируя слагаемые, относящиеся к одному подпространству, получим равенство вида

x1 + x 2 + ... + x s = q ,

где хотя бы один вектор отличен от нулевого. Пусть, для опреде- лённости x1 ¹ q , тогда

x1 = -x 2 - ... - x s ,

т.е. ненулевой вектор x1 Î L1 принадлежит и сумме L2 + ... + Ls , что

32

противоречит свойству 3.

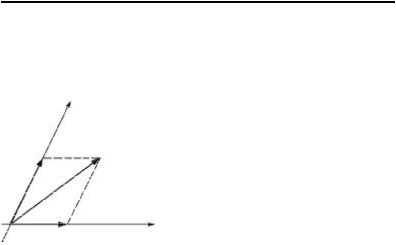
Замечание. Если сумма двух подпространств L ′ и L ′′ прямая, т.е. L = L ′ Å L ′′ , тогда их пересечение нулевое L ′ I L ′′ = {q} (рис. 9.2).

Заметим так же, что сложение подпространств обладает свой- ством ассоциативности, т.е.

базис e1,e2 ,...,ek . На основании предложения 9.10 мы можем до- полнить этот базис до базиса пространства L n векторами ek +1,ek +2 ,...,en , которые можно взять в качестве линейной оболоч- ки L ′′ . На основании предложения 9.17 п.4 можем записать

L = L ′ Å L ′′ .

ТЕОРЕМА 9.2. Размерность суммы двух подпространств равна

сумме их размерностей минус размерность их пересечения

да на основании предложения 9.18 найдётся такое подпростран- ство M , что