3. Линейные дифференциальные уравнения второго порядка.

Линейные дифференциальные уравнения второго порядка теории дифференциальных уравнений занимает важное место не только потому, что они представляют простой и хорошо изученный тип уравнений, но и в связи с тем, что значительное колличество практических задач физики, механики, техники и особенно электротехники приводят к решению уравнений.

1. Основные понытия.Определение. Уравнения вида

y’’+p(x)y’+q(x)y=f(x) (1)

где у – искомая функция, p(x),Q(x),f(x) непрерывные функции на некотором интервале (а,б) называется линейным дифференциальным уравнением второго порядка.

Если f(x)=0 то уравнение (1) называется линейно однородным уравнением. Еслиf(x)0 то уравнение (1) называется линейно неоднородным уравнением.

Разрешая уравнение 1 относительноy’’:y’’= -p(x)y’ –q(x)y+f(x), видим что оно является частным случаем уравненияy’’=f(x,y,y’). Следовательно уравнение 1 удовлетворяет условиям теоремы о существовании решения. Действительно, функцияf(x,y,y’)= -p(x)y’ –q(x)y+f(x) непрерывна как функция трех переменных x, y,y’ частные производныеf’_y(x,y,y’)= -q(x) ,f’_y’(x,y,y’)= -p(x) также являются непрерывными функциями трех переменных. Поэтомупри любых начальных условиях

Где х₀(а,б), уравнение 1 имеет единственное решение задачи Коши, удовлетворяющее этим условиям.

2. Линейные однородные дифференциальные уравнения второго порядка.

Рассмотрим некоторые свойства решений линейных однородных уравнений.

Теорема 15.3если функция у₁(х) и у₂(х) – решения уравнения

y’’+p(x)y’+q(x)y=0 (2)

то функция при любых значениях постоянных С₁С₂ также является решением уравнения 2.

Доказательство. Продифференцировав дважды функцию у=С₁у₁(х)+ С₂у₂(х) и подставив выражения дляy,y’,y’’ в левую часть уравнения 2 получим

Так как функции у₁(х) и у₂(х) по условиям являются решениями уравнения 2 то выражение в квадратных скобках тождественно равно нулю а это значит что функция у=С₁у₁(х)+ С₂у₂(х) является решением уравнения 2.

Итак доказано что функция вида у=С₁у₁(х)+ С₂у₂(х) с произвольными постоянными С₁ и С₂ являются решением уравнения 2. Естественно возникает вопрос не является ли это решение общим решением уравнения 2. Будет доказано что при некоторых условиях функции у=С₁у₁(х)+ С₂у₂(х) является общим решением уравнения 2. Для выяснения этих условий введем понятие линейной зависимости и линейной независимости функций у₁(х) и у₂(х).

Функции у₁(х) и у₂(х) называются линейно-зависимыми на (а,б) если существуют такие числа а₁и а₂из которых хотя бы одно отличалось от нуля, для любого х из интервала (а,б) имеет место равенство

а₁у₁(х)+ а₂у₂(х)=0. (3)

очевидно что если функции у₁(х) и у₂(х) линейно зависимы то они пропорциональны. Действительно если а₁у₁(х)+ а₂у₂(х)=0 причем а₁0 и у₂0 то у₁(х)/ у₂(х)= - а₂/а₁=const. Верно и обратное.

Функции у₁(х) и у₂(х) называются линейно-независимыми на (а,б) если не существует таких чисел из которых хотя бы одно отлично от нуля что для любого х из интервала имеет место равенство 3.

Другими словами равенство 3 выполняется сразу для всех только если а₁=а₂=0.

Очевидно что если функции у₁(х) и у₂(х) линейно независимы то их соотношение у₁(х)/ у₂(х)constт.е. они не пропорциональны. Так например функции у₁(х)=х²и у₂(х)=х³линейно-независимы на любом интервале (а,б) так как у₁(х)/у₂(х)=1/хconstа функции у₁(х)=4х²у₂(х)=х² линейно-зависимы в любом промежетке так как у₁(х)/у₂(х)=4=const.

Предположим теперь что функции у₁(х) и у₂(х) являются решением уравнения 2. Как узнать являются ли они линейно-зависимыми или линейно-независимыми. Удобным аппаратом для исследования этого вопроса является так называемый определитель Вронского составленный из этих решений

Определитель Вронского является функцией определенной на (а,б) и обозначается W(у₁,у₂) или простоW(x).

Теорема 15,4.Если функции у₁(х) и у₂(х) линейно-зависимы на (а,б) то определитель Вронского составленный из них равен нулю на этом интервале.

Доказательство.Так как по условию функции у₁(х) и у₂(х) линейно-зависимы то по определению существует числа а₁и а₂ из которых одно обязательно отлично от нулю такие что имеет место равенство 3: а₁у₁(х)+ а₂у₂(х)=0. Пусть например а₁0. Тогда из равенства 3 следует что

Подставляя выражения для у₁(х) и у’₁(х) в определитель Вронского получим

Теорема 15,5.Если решения уравнения 2 линейно-независимы на (а,б) то определитель Вронского составленный из них отличен от нуля на этом интервале.

Д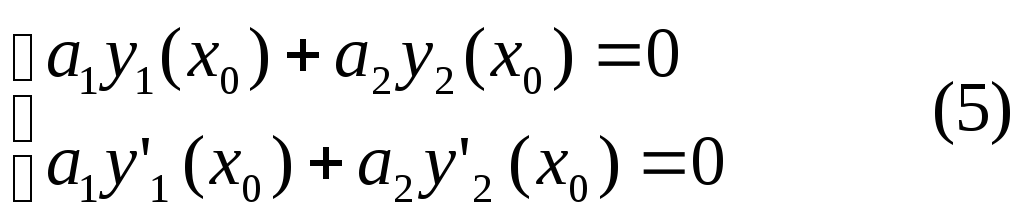оказательство.Допусти обратное т.е. предположим что существует точка х₀(а,б) в которой определитель Вронского =0. Составим систему уравнений

В которой а₁и а₂ – неизвестные числа. Ток как определитель этой системыW(х₀)=0 то система 5 имеет нулевое решение а₁и а₂. Рассмотрим функцию

у=а₁у₁(х)+ а₂у₂(х)

по теореме 15,3 эта функция является решением уравнения 2. Кроме того поскольку а₁и а₂ – решения системы 5 то функция у(х) удовлетворяет нулевым начальным условиям

таким начальным условиям очевидно удовлетворяет решение у(х)=0. По теореме о существовании и единственности решения, решение у(х)=0 является единственным решением уравнения 2 с начальными условиями 6. Следовательно а₁у₁(х)+ а₂у₂(х)=0 а это означает что функции у₁(х) и у₂(х) линейно-зависимы на (а,б) что пртиворечит условию теоремы. Таким образомW(х)для всех х(а,б).

Итак установлено что если функции у₁(х) и у₂(х) являются на (а,б) решениями линейного однородного уравнения 2 то составленный из них определитель Вронского равен нулю либо отличен от нуля на (а,б).

Теперь мы можем доказать при каких условиях функция у=а₁у₁(х)+ а₂у₂(х) будет общим решением линейно однородного уравнения 2.

Теорема 15,6.Если функции у₁(х) и у₂(х) – линейно-независимы на (а,б) решения уравнения 2 то функция

у=С₁у₁(х)+ С₂у₂(х) (7)

где С₁С₂ произвольные постоянные являются общим решением уравнения 2 на (а,б).

Доказательство.Прежде всего напомним что в силу теоремы 15,3 функция у=С₁у₁(х)+ С₂у₂(х) при любых значениях постоянных С₁С₂ является решением уравнения 2. Для того чтобы доказать что эта функция является общим решением уравнения 2 достаточно установить что из него можно выделить частное решение удовлетворяющее заданным начальным условиям.

Пусть х₀(а,б) и

- произвольные начальные условия. Покажем что произвольные постоянные С₁С₂ можно подобрать так что решение 7 при этих значениях постоянных будет частным решением удовлетворяющим заданным начальным условиям 8.

Составим систему уравнений:

В которой С₁С₂ – неизвестные числа. Определитель этой системы естьВронскогоW(х₀). Так как по условию функции у₁(х) и у₂(х) – линейно-независимы на (а,б) то в силу теоремы 15,5W(х₀). Поэтому система 9 имеет единственное решение которое обозначим С₁= С⁰₁С₂= С⁰₂. Подставляя С⁰₁ и С⁰₂ в равенство 7 получим искомое частное решение уравнения 2 у= С⁰₁у₁(х)+ С⁰₂у₂(х) удовлетворяющее условиям 8. Это и означает, что решение 7 является общим решением уравнения 2.

Из доказанной теоремы следует, что для отыскания общего решения уравнения 2 достаточно найти два линейно-независимых частных решения и составить выражение 7 с произвольными постоянными.

Пример 1.Рассмотрим уравнениеy’’-y=0

Имеем линейное однородное уравнение. Легко заметить что частными решениями будут у₁(х)е^ху₂(х)е^-х. Так как определитель Вронского

Отличен от нуля то эти решения линейно-независимы на всей числовой прямой. Следовательно общее решение данного уравнения можно записать в виде у=С₁е^х+ С₂е^-хгде С₁С₂ - произвольные постоянные.

В заключении покажем как можно найти общее решение уравнения 2 если известно только одно частное решение этого уравнения.

Пусть у₁(х)- частное решение уравнения 2. Введем новую функциюzполагаяy= у₁z. Тогдаy’= у’₁z+у₁z’,y’’= у’’₁z+2у’₁z’+у₁z’’. Подставляя выражение дляy,y’,y’’ в уравнение 2 и группируя слагаемые получаем

Так как у₁(х) – решение уравнения 2 то выражение в первых квадратных скобках равно нулю и уравнение имеет вид

Порядок этого уравнения можно понизить положивz’=uгдеu– новая искомая функция

Получили уравнение первого порядка с разделяющимися переменными относительно функцииu. Решая его находим

Где С₁ произвольная постоянная. Возвращаясь к первой переменнойzи умножая выражение дляzна у₁ получаем общее решение уравнения 2