1 Интегрирование рациональных дробей

1.1 Теоретическое введение

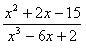Рациональной дробью называется отношение двух многочленов: гдеa₀, a₁, ..., a_n, b₀, b₁, ..., b_n – действительные числа. Рациональная дробь называется правильной, если степень числителя строго меньше степени знаменателя (n < m), в противном случае (n ≥ m) – дробь называется неправильной. Например, дробь – правильная, а дроби– неправильные. У любой неправильной дроби можно выделить ее целую часть, т.е. представить ее в виде суммы многочлена и правильной дроби. Всякая правильная дробь может быть представлена в виде суммы конечного числа простейших дробей следующих четырех типов: 1); 2)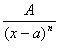(n > 1 –натуральное число); 3) ; 4)(n > 1 – натуральное число,p² – 4q < 0, т.е. многочлен, стоящий в знаменателе не имеет действительных корней).

1.1.1 Схема интегрирования рациональных дробейДля интегрирования рациональной дроби необходимо: 1) Если дробь неправильная – представить ее в виде суммы многочлена и правильной дроби. 2) Разложить правильную дробь на сумму простейших дробей. 3) Найти интеграл многочлена и всех простейших дробей.

1.1.2 Интегрирование простейших рациональных дробей Простейшая дробь первого типа: Простейшая дробь второго типа: Простейшая дробь третьего типа: Вычисление интеграла от нее заключается в интегрировании квадратного трехчлена в знаменателе. 1) Выделим полный квадрат суммы в знаменателе подынтегральной функции.2) Выполним замену переменной, приняв выделенный двучленх + 2 за новую переменную. Далее для удобства следующих преобразований выразим х через переменную t. 3) Выполним почленное деление числителя на знаменатель и представим полученный интеграл в виде разности двух интегралов.4) Первый интеграл вычислим с помощью метода замены переменной, взяв за новую переменнуюt знаменатель подынтегрального выражения, второй интеграл является табличным. Таким образом,

1.1.3 Выделение целой части у неправильной дроби Любую неправильную дробь можно представить в виде суммы многочлена и остаточной правильной дроби. Для этого необходимо по правилу деления многочленов разделить числитель на знаменатель. Искомым многочленом является результат деления, числителем правильной дроби – остаток деления, знаменателем – делитель. Пример.Решение Так как степень числителя (3) выше степени знаменателя (1), то данная дробь является неправильной. Разделим числитель на знаменатель по правилу деления многочленов. Таким образом,

1.1.4 Разложение правильной дроби на сумму простейших дробей Любой многочлен Q_m(x) с вещественными коэффициентами разлагается (и притом единственным способом с точностью до перестановки сомножителей) на произведение множителей первой степени вида (х – а) и множителей второй степени вида (x² + px + q). Разложение правильной дроби на сумму простейших дробей зависит от того, каким образом многочлен Q_m(x), стоящий в знаменателе, раскладывается на множители. Рассмотрим различные варианты разложения. 1) Знаменатель раскладывается лишь на неповторяющиеся множители первой степени вида (х – а). В этом случае в разложении правильной дроби на сумму простейших каждому неповторяющемуся множителю первой степени соответствует слагаемое вида , гдеА – неизвестный числовой коэффициент, который необходимо найти в дальнейшем ходе решения. (n < m ) 2) Знаменатель раскладывается лишь на множители первой степени, среди которых есть повторяющиеся. В этом случае в разложении правильной дроби на сумму простейших каждому повторяющемуся r раз множителю соответствуют слагаемые гдеA₁, A₂, ..., A_r-1, A_r – неизвестные числовые коэффициенты, которые необходимо найти в дальнейшем ходе решения. 3) Знаменатель раскладывается на множители второй степени вида (x² + px + q) и, возможно, множители первой степени. Под множителем второй степени мы будем понимать многочлен вида (x² + px + q) без действительных корней, т.е. D = p² – 4q < 0. Каждому неповторяющемуся множителю второй степени в разложении правильной дроби на простейшие соответствует слагаемое , гдеА и В – неизвестные числовые коэффициенты.