
- •Глава 2. Производная. §1.Задачи, приводящие к понятию производной. Определение.
- •§2. Свойства дифференцируемых функций.
- •§3. Правила дифференцирования.
- •§4. Таблица производных.
- •§6. Логарифмическая производная.
- •§7. Лемма Фермá.
- •§8. Теоремы о среднем значении.
- •§9. Правило Лопиталя-Бернулли раскрытия неопределённостей вида и.
- •§10. Производные и дифференциалы старшего порядка.
- •§11. Формула Тейлора.
- •§12.Таблица основных разложений по формуле Маклорена.
§9. Правило Лопиталя-Бернулли раскрытия неопределённостей вида и.
Теорема (Г.Ф.А. Лопиталь 1661-1704, И. Бернулли 1667 − 1748). Пусть выполнены условия:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() (случай неопределённости вида
(случай неопределённости вида
![]() ).
Тогда
).
Тогда
 −правило Л-Б.
−правило Л-Б.
Обратная импликация неверна.
Доказательство.
Пусть
![]() .
Можно считать, что
.
Можно считать, что![]() и
и![]() .
Тогда по теореме Коши, будем иметь
.
Тогда по теореме Коши, будем иметь![]() ,
где
,
где![]() .
Поэтому
.
Поэтому![]() правая часть последнего равенства будет
стремиться
правая часть последнего равенства будет
стремиться![]() .
Следовательно, левая часть равенства,
то есть
.
Следовательно, левая часть равенства,
то есть![]() ,
,![]() также будет стремиться к
также будет стремиться к![]() .
.
То, что обратная импликация неверна, видно из следующего контрпримера.
Контрпример.
Пусть
![]() .
Тогда
.
Тогда![]() в то время, как предел
в то время, как предел![]() не существует.
не существует.
Замечание 1. Правило Л.-Б. справедливо и для пределов слева.
Замечание 2. Можно
доказать, что правило Л-Б применимо и
тогда, когда
![]() ,
а также в случае неопределённости вида
,
а также в случае неопределённости вида![]() .
.
§10. Производные и дифференциалы старшего порядка.
![]() Рекуррентное определение:
Рекуррентное определение:
![]() .Точно так же
.Точно так же
![]() .
.
Пример 1.
 .
.
Пример 2.
![]() ;
;
![]() .
.
Мы видим, что формулы для второй и третьей производных произведения имеют ту же структуру, что и формулы для квадрата суммы, куба суммы.
Упражнение. Доказать
с помощью ММИ, что формула для n-й
производной
произведения устроена так же, как
биномиальная формула Ньютона:
![]() .Именно:
.Именно:
![]() (правило Лейбница).
(правило Лейбница).
|
Так
называемые биномиальные
коэффициенты
(Б. Паскаль: 1623 − 1662) |
1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1 1 8 28 56 70 56 28 8 1 1 9 36 84 126 126 84 36 9 1 …………………………………… Треугольник Паскаля |
![]() .
Если
.
Если
![]() − независимая переменная, то
− независимая переменная, то
![]() .
.
Замечание. Этим
объясняется еще одно обозначение для
производной второго порядка:
![]() (для производнойn-го
порядка −
(для производнойn-го
порядка −
![]() ).
).
Пусть снова
![]() .
Произведём замену переменной
.
Произведём замену переменной![]() (теперь уже
(теперь уже![]() − зависимая переменная). В этом случае
− зависимая переменная). В этом случае
![]()
![]() .
.
Таким образом, запись
2-го дифференциала
![]() не является инвариантной
относительно замены независимой
переменной (тем более, не инвариантна
запись
не является инвариантной
относительно замены независимой
переменной (тем более, не инвариантна
запись
![]() дляn-го
дифференциала).
дляn-го
дифференциала).
§11. Формула Тейлора.
Задача. Дана функция![]() ,
имеющая
,
имеющая![]() производных в окрестности точки
производных в окрестности точки![]() .
Подобрать алгебраический многочлен
.
Подобрать алгебраический многочлен![]() степени
степени![]() такой, что
такой, что![]() .
.
Решение.Это − многочлен ,
в краткой записи
,
в краткой записи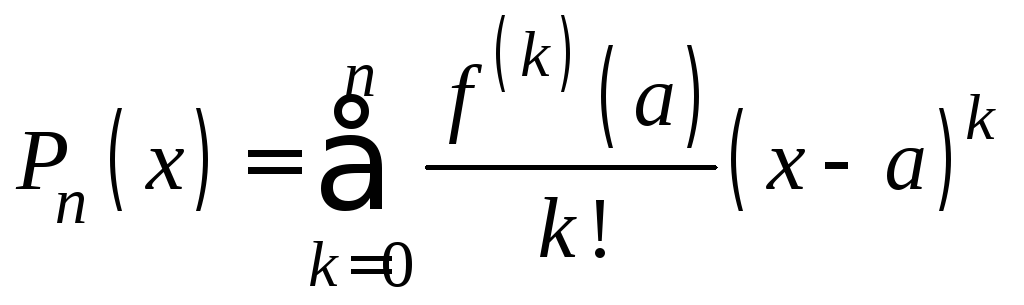 .
Многочлен
.
Многочлен![]() называетсяn-м
многочленом Тейлорафункции
называетсяn-м
многочленом Тейлорафункции![]() .
.
Доказательство.Ясно, что
![]() .
Далее,
.
Далее,
 .
.
Поэтому
![]() .
Ч. и т. д.
.
Ч. и т. д.
Замечание 1. Из линейной независимости
системы степенных функций![]() следует единственность решения
рассматриваемой задачи.
следует единственность решения
рассматриваемой задачи.
Для того, чтобы понять насколько хорошо
многочлен Тейлора приближает исходную
функцию, необходимо изучить так наз.
остаточный член![]() .
Равенство
.
Равенство

называют формулой Тейлора с остаточным
членом![]() .
Изучим величину
.
Изучим величину![]() .
.
Теорема. Если функция![]() принадлежит классу
принадлежит классу![]() ,
то есть имеет непрерывные производные
прядка
,
то есть имеет непрерывные производные
прядка![]() на отрезке
на отрезке![]() ,
то для любого
,
то для любого![]() ,
принадлежащего этому отрезку, существует
такое число
,
принадлежащего этому отрезку, существует
такое число![]() ,
заключенное между числами
,
заключенное между числами![]() и
и![]() ,
что остаточный член
,
что остаточный член![]() может быть представлен в виде
может быть представлен в виде
 (остаточный член
в форме Лагранжа).
(остаточный член
в форме Лагранжа).
Доказательство.Положим![]() .
Тогда, очевидно, будет
.
Тогда, очевидно, будет![]() ,
,![]() .
Кроме того,
.
Кроме того,![]() ,
,![]() .
Применяя многократно теорему Коши о
среднем значении, получим
.
Применяя многократно теорему Коши о
среднем значении, получим



 ,
,
|
где
|
|
Следствие. При тех же условиях можно утверждать, что
![]() (остаточный член вформе Пеано).
(остаточный член вформе Пеано).
Замечание 2.Если несколько усложнить
рассуждения, то можно доказать последнее
утверждение при условии, что![]() существует
существует![]() (и, разумеется, производные меньших
порядков
(и, разумеется, производные меньших
порядков![]() существуют в окрестности этой точки).
существуют в окрестности этой точки).
Замечание 3. Частный случай формулы
Тейлора, когда![]() ,
принято называтьформулой
,
принято называтьформулой
Маклорена.
(Б. Тейлор 1685 − 1731; К. Маклорен 1698 −1746).

 .
.