Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Ульяновское Высшее Авиационное Училище Гражданской Авиации

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ЭКОНОМЕТРИКА и математическая экономика / Шананин А.А. Математические модели в экономике. 1999

.pdf

Скачиваний:

176

Добавлен:

20.04.2015

Размер:

467.72 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 66

3.3.1 Модель олигополической конкуренции Курно

N = {1, ..., n} — множество производителей. X — набор товаров.

P (X) — обратная функция спроса, которая показывает, по какой цене производители согласны купить набор товаров X.

P (X) удовлетворяет условию:

A1	P (X) C2, P 0(X) < 0, P (0) > 0
	M > 0 : P (M) = 0, M — максимальный объем продажи товара (объем насыщения).

Производитель описывается функцией издержек:

ci(x) — функция издержек i-го производителя (какие затраты должен сделать производитель что бы выпустить товар в объеме X, имеются ввиду денежные затраты).

ci(x) удовлетворяет условию:

A2	i Nci(x)				2 C2
		dci(x)	> 0,	d ci(x)		> 0	— выпуклость ci.
		dx			dx2

Основная идея заключается в том, что чем больше товаров мы берем, тем меньше платим. Опишем поведение i-го производителя:

xi — выпуск i-го производителя, xi [0, M].

X = xj — суммарный выпуск.

j=1

Выбор стратегии определяет прибыль производителя:

ui(~x) = P ( xj)xi − ci(xi) — прибыль i-го производителя (его целевая функция). Можно

j=1

заметить, что на прибыль влияет суммарный выпуск.

Получили игру в нормальной форме. Компромиссом является равновесие по Нэшу.

Теорема. Пусть выполнены условия A1 и A2 и кроме того, будем считать, что функция P (X)X является выпуклой. Тогда в модели Курно существует и единственное равновесие по Нэшу.

P.S. Если P (X) вогнута, то и P (X)X вогнута (P 00(X) 6 0)

(P (X)X)00 = P 00(X)X + 2P 0(X) =	P 00(X)X	6	0).
		6

Доказательство. Существование

[0, M] — множество стратегий i-го игрока — выпуклый компакт (выполнено 1-ое условие теоремы Нэша).

ui(~x) — непрерывная функция по совокупности переменных (x1, ..., xn) (выполнено 2-ое условие теоремы Нэша). Покажем, что ui(xi, ~x−i) вогнута по xi при условии, что стратегии всех остальных игроков фиксированны. Так как существует вторая производная, то надо показать, что она неположительна.

∂2u (x

, ~x

)

d2c

(x )

i i

−i

= P 00(

x )x + 2P 0(

x )

∂x2

j i

j −

dx2

j=1

}

Достаточно доказать, что

X	X
P 00(	xj)xi + 2P 0( xj) 6 0	(1)
j=1	j=1

1. Если P 00( P xj) 6 0, то (1) очевидно

j=1

	n
2. Если P 00(	jP
2. Если P 00(	xj) > 0, то можно сделать следующую оценку:
	=1
n	n	n	n	n
X	X	X	Xj	X
P 00( xj)xi + 2P 0(		xj) 6 P 00(	xj)	xj + 2P 0( xj) 6 {P (X)X — вогнута} 6 0
j=1	j=1	j=1	=1	j=1

= по теореме Нэша существует равновесие по Нэшу в модели Курно.

Единственность

Пусть есть еще одно равновесие по Нэшу (x1, ..., xn).

Обозначим G = P xj — суммарный выпуск.

j=1

Мы знаем, что

u (x , ~x

) =

max

P (x +

(x )

i −i

[0,M]

{

i −

}

i6=j

Без ограничения общности можно считать, что M = ∞ (при xi > M прибыль становится отрицательной максимум будет тот же). Производная функции в точке максимума равна нулю:

P 0(G)x + P (G)

−

dci(x )

= 0,

еслиx > 0

dxi

P 0(G)x + P (G)

−

dci(x )

еслиx = 0

dxi

Задача дополнительности для i-го производителя:

P 0(G)x + P (G)

dci(xi)

dxi

(2)

( xi[P 0(G)xi + P (G)

−

dci(xi)

]

= 0

−

dxi

В первом неравенстве P 0(G)x < 0 и

dci(xi)

0. Для i-го производителя его оптимальное

dxi

решение является решением задачи дополнительности ( i). Как устроено решение задачи дополнительности? Есть два варианта:

1.Производитель ничего не выпускает он избыточен.

2.Он выпускает ровно столько, что выполняются все условия.

Решение (2) определяет функцию xi(G) — определяет однозначно, т.е. она единственна. При

нашем предположении о том, что P 0(G) < 0 и

dci(xi)

P 0

(G)x + P (G)

−

dci(xi)

dxi

— монотонно убывает по xi, при

фиксированном, причем в пределе при

→ ∞

функция

dc (x )

стремится к −∞. Так как P 0(G)xi + P (G) −

i i

монотонно убывает, то возможны два

dxi

варианта:

1. или

xi(G) : P 0(G)xi + P (G) −

dc (x

)

= 0

(?)

i i

dxi

2. или

xi(G) = 0

Обозначим: I(G) = {i |

xi(G) > 0} — те фирмы которые что-то выпускают.

Продифференцируем (?):

P 00(G)x

(G) + P 0

(G)

dxi(G)

+ P 0(G)

d2c

dxi(G)

= 0

− dxi

dxi(G)

P 00(G)xi(G)+P 0(G)

d2ci

− P 0(G)

| {z }

|{z}

Видно, что знаменатель никогда не обращается в ноль. Введем еще два обозначения:

I+(G) = {i I(G) |

dxi(G)

> 0}

I−(G) = {i I(G) |

dxi(G)

I+(G)

— агенты которые при увеличении G ведут себя агрессивно.

I−(G)

— агенты которые при увеличении G ведут себя пассивно.

Если

i I+(G),

то

0 6

dxi(G)

−1 − xi(G)

P 00(G)

P 0(G)

Если

i I−(G),

то

− 1 − xi(G)

P 00(G)

dxi(G)

6 0

P 0(G)

P (G)G – вогнута

P 00(G)G + 2P 0(G)

P 00(G)

−

, i I0(G)

xi(G) > 2

P 0(G)

{Один агент не может контролировать более половины рынка}

= |I − +(G)| 6 1

Хотим доказать, что G − xi(G) = 0, то есть хотим доказать, что эта величина монотонна.

i=0

Просуммируем по всем

агентам, которые хоть что-то производят:

1 −

dxi(G)

> 1 −

i I(G)

i I+(G)

1. |I+(G)| = 0,

dGd [G −

=1 xi(G)] > 0

dxi(G)

P 00(G)

2. |I+(G)| = 0,

dG > 2 − xi(G) P 0(G) > 0

1 −

i I+(G)

= решение модели Курно единственно.

3.3.2Монополия

Производитель один и он распоряжается всеми производственными мощностями. Введем некоторые обозначения:

n	n
X	X
c(x) = min{ ci(xi) \|	xi = x, xi > 0, i = 1, ..., n}
i=1	i=1

— суммарная функция издержек, можно заметить, что каждый выпуск > 0. Монополист хочет максимизировать объем, что бы издержки были минимальными. Эту функцию можно представить в таком виде:

c(x) = c1(x)

...

cn(x)

выпукла, то и

в выпуклом анализе функция такого вида

называется конволюцией. Если

c(x)

M M

все ci(x) выпуклы. Усилим требования на ci(x):

A20

i N ci(x) C2,

dci(x)

> 0,

d2ci(x)

< 0

dx2

Задача. Доказать, что c(x) дифференцируема.

Лемма. Пусть x1(x), ..., xn(x)) решение задачи:

Pi=1 xi = x−→

min

i=1 ci

(xi)

> 0, ..., xn > 0

тогда, если xj(x) > 0, то

dcj(xj(x))

dc(x)

dxj

Доказательство. Составим функцию Логранжа и воспользуемся теоремой Куно-Таккера:

L(~x, λ) = sumni=1ci(xi) + λ[x − xi]

i=1

Если xj(x) > 0, то dcj(xj(x)) = λ

dxj

Введем обозначение:

I(x) = {i | xi(x) > 0}

тогда

c(x) =

ci(xi(x)) +

ck(0)

i I(x)

k /I(x)

dc(x)

= i PI(x)

dc (x (x)) dxi(x)

= λ i PI(x)

dxi(x)

i i

dxi

∂xi(x)

= {x = i PI(x) xi(x)

– дифференцируем по

1 = i PI(x)

} = λ

∂x

Замечание. Если фирма ничего не выпускает (xj(x) = 0), то предельные издержки должны

быть выше чем (

dcj(0)

dc(x)

dxj

Лемма.

dc (x )

6 j I(x )

j I(x)

dxj

Pdx

x )

dxj

min

dc(

max

i=1 i

Здесь x , ..., x — равновесие по Нэшу вмодели Курно, x =

x , I(x ) =

{

x > 0

}

Доказательство.

ci(xi)| n

xi = x, xi 6 0)

c(x) = min ( n

xi(

xj ) 6= xi

i=1

Пусть

dc (x )

dci

j=1 xj !!

dxi

a)xi

j=1 xj !

dxi

> 0

)

dci

j=1 xj !

(x )

dxi

Из вогнутости следует, что

	n
xi	Xj	xj	< xi
xi		xj	< xi
	=1

b)xi	j=1 xj !	= 0 6 xi
	n
	P

n		n			n
Xi	xi	X	xj	<	X
	xi		xj	<	xi
=1		j=1			i=1

P (xc) =

P (x)x − c(x) −→ max — монополист максимизирует свою прибыль.

χµ — решение задачи дополнительности, χµ > 0 :
( χµ[P 0(χµ)χµ + P (χµ) −c(χµ)		] = 0
P 0(χµ)χµ + P (χµ)	c(χµ)		6	0
	dχ
−
	dχ

3.3.3 Совершенная конкуренция

pxi − ci(xi) −→ maxxi>0 — для каждого производитьеля.

p – цены, i = 1, ..., n. p считаем фиксированным, находим xi, xˆi(p) – решение задачи.

Определение. pc — назвается ценой совершенной конкуренции, если

P ( xˆi(pc)) = pc

i=1

xc = xˆi(pc) — выпуск в условиях совершенной конкуренции.

i=1

Задача. Если xc является выпуском в условиях совершенной конкуренции, то dc(xc)

{Предельные издержки установятся на уровне цены}

Из этого упражнения следует следующий факт: xµ < xc

Доказательство.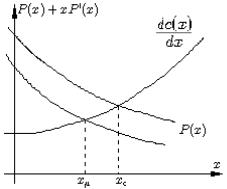

Рис. 3.3:

На рисунке 3.3 дана иллюстрация.


P (X) −	dc(x)	— монотонно убывает. Достаточно доказать, что P (xµ) −						dc(xµ)	> 0 т.к.
P (X) −	dx	— монотонно убывает. Достаточно доказать, что P (xµ) −						dxµ	> 0 т.к.
		xµ < xv		P (xµ) −		dc(xµ)	> 0
		xµ < xv		P (xµ) −		xµ	> 0
А это верно, так как			dc(xµ)
			dc(xµ)
		P (xµ) −			= −xµP 0(xµ) > 0
		P (xµ) −	xµ		= −xµP 0(xµ) > 0

Рассмотрим {p~ , ~x1, ..., ~xm, ~y1 , ..., ~yn} :

1) ˜

j = 1, ..., n ~yj ψj(p~ ) = arg max p~ ~y

~y Yi

2) i = 1, ..., m ~xi ϕ˜i(p~ ) = arg max{ui(vx) | p~ ~x 6 p~ w~(i) + P αijπ˜j(p~ ), ~x 6 0}

m	m	n
Xi	X	X
~xi 6		w~(i) + ~yi
=1	i=1	j=1
m	n	m

(3.1)

XX X

(p~ ,	w~(i) +	~yj −	~xi ) = 0	(3.2)
	i=1	j=1	i=1

3.3.4 Модификация функций спроса и предложения.

Теорема (Эрроу–Дебре). Пусть выполнены следующие условия :

P1	Yj являются выпуклыми замкнутыми множествами, 0 Yj (j = 1, ...n)
C1	ui(~x) – вогнутая непрерывная на R+l ненасыщаемая функция (i = 1, ..., n)
C2	w~(i) > 0 (i = 1, ..., m)
	n
P2	Y = j=1 Yj – алгебраическая сумма множеств, Y ∩ R+l = {0} (условие отсутствия
	рога изобилия)P
P3	Y ∩ (−Y ) = {0} (условие необратимости технологических процессов)
	m
C-P	P αij = 1 (j = 1, ..., n) (прибыль производителей полностью распределена между по-

i=1

требителями),

тогда существует конкурентное равновесие.

Рассмотрим для каждого производителя вспомогательное множество :

m			X
X		(i)	X
˜	w~	(i)	+ ~yk + ~y > 0, ~yk Yk k 6= j}
Yj = {~y Yj\|	w~		+ ~yk + ~y > 0, ~yk Yk k 6= j}
i=1			k6=j

— множество наборов, которые могут быть реализованы, используя запасы потребителя и технологии так, что ~y обеспечивается ресурсами. Если реализуется конкурентное равновесие,

то ˜ (из (3.1)) ограничимся только теми наборами, которые могут быть реализованы,

~yj Yj

т.е.

				m				n
	˜			Xi		(i)		X
	X = {~x > 0 \| ~yj Yj (j = 1, ..., n)				w~		+	~yj > ~x}		(3.3)
				=1				j=1
Лемма.	Множества	˜ ˜
Лемма.	Множества	Yj, X являются ограниченными.
			˜	– ограничено, т.к. в (3.3) w~					(i)	– фиксировано,
Доказательство. Достаточно доказать, что Yj				– ограничено, т.к. в (3.3) w~						– фиксировано,
		˜	˜
~yj – ограничено в силу ограниченности Yj X – ограничено.

Докажем ограниченность всех ˜ от противного :

X	X
~yj(ν) Yj	w~(i) + ~yj(ν) > 0	(3.4)
i=1	j=1

Пусть

µ(ν) =

max ~y (ν)

> 0

16j6n k

νlim µ(ν) = +∞

(3.5)

Поделим (3.4) на µ(ν)

→∞

~yj(ν)

> 0

µ(ν)

w~(i) +

µ(ν)

(3.6)

j=1

по построению

~yj(nu)

1 последовательность ограничена, следовательно можно выделить

µ(ν)

сходящуюся

подпоследовательность :

~yj(ν(t))

lim

= ~yj

(3.7)

t→∞ µ(ν(t))

По предположению Yj – выпукло :

~yj(ν(t))

~yj

1 −

0 Yj, т.к. 0, ~yj

Yj, 0 <

< 1 ( в силу (3.5) )

µ(ν(t))

Переходя к пределу в (3.6), получим

– замкнуто ~yj Yj

(3.8)

~yj >

По построению µ(ν) по крайней мере при одном j

~yj(ν)

= 1

µ(ν)

: ~y

= 0

(3.9)

существует по крайней мере одно

Воспользуемся предположениями теоремы Эрроу–Дебре.

n ˆ

= 0

По условию P2 (Y ∩ R+ = {0}) j=1 ~yj

= ~ys +

~yj + 0 −Y

(по (3.8)) ~ys Y ∩ (−Y ) по P3

~ys

k6=s

0 Y =

Yj −~ys =

j6=s

~ys = 0, что противоречит (3.9)

Выберем достаточно большой замкнутый параллелепипед E Rl Хотим, чтобы

int E

(3.10)

Yj int E, X int E, 0

E = {~x |~a

6 ~xb}, a и b выбирем из (3.10) (это можно сделать, т.к. X и

Yj – ограничены).

Рассмотрим вспомагательные задачи, в которых можество затрат–выпусков ограничено параллелепипедом E.

ψj(p~) = arg max p~y. Этот максимум достигается, т.к. Yj ∩ E – компакт, p~y – линейная непре-

~y Yj∩E

рывная функция.

πj(p~) = max p~y

y~ Yj∩E

Функцию спроса и предложения можно переписать в виде :

ϕi(p~) = arg max{ui(~x) \| ~x > 0 и p~x 6 p~w(i) +				n
ϕi(p~) = arg max{ui(~x) \| ~x > 0 и p~x 6 p~w(i) +				=1 αijπj(p~), ~x E}
Функция избыточного предложения :				jP
χ(p~) =	m	m	n
χ(p~) =	=1 w~(i) + j=1		ψj(p~) − i=1 ϕi(p~)
	iP	P	P

Лемма. Пусть p~ > 0, p~ 6= 0 такой, что χ(p~ ) ∩ Rl+ 6= , тогда существует конкурентное равновесие с ценами p~

Доказательство. ~xi ϕ(p~ ),

~yj ψ(p~ )

=1 w~(i) + j=1 ~yj − i=1 ~xi > 0

{

является конкурентным равновесием.

iPp~ , ~x , ...,P~x

, ~y

, ...P, ~y

Докажем, что ~yj ψ˜j(p~ ) от противного :

~yj Y˜j intE

по построению ~y˜j

: p~ ~y˜j

> p~ ~yj

~y(t) = t~y

+ (1

−

t)~y˜

p~ ~y(t) > p~ ~y

(0, 1]

0 < t < 1: ~y(t) Yj ∩ E, что противоречит ~yj ψ(p~ )

~y ψ˜j(p~ ), πj(p~ ) = π˜j(p~ )

Докажем, что ~xi ϕ˜i(p~ ) :

~x˜

0, p~ ~x

p~w(i)

π˜

(p~) и u (~x˜) > u

(~x )

предположим противное

~x(t) = t~x

+ (1

−

t)~y

0 t

(0, 1]

По неравенству Иенсена для вогнутых функций :

u (~x(t))

(~x ) + (1

−

t)u (~x˜) > u

(~x ) t

(0, 1]

~xi X˜ intE

0 < t0 < 1 : ~x(t0) E

p~ ~x(t)

p~ w~ +

π˜

(p~), т.е. ~x(t)

~x,˜ ~x – удовлетворяют бюджетным ограничениям

j=1

, т.к.

тоже удовлетворяет бюджетным ограничениям

что

~xi

ϕ(p~ )

противоречие с те,P

нашли точку, которая лучше.

w~(i)[s] +

~y [s]

~x [s] = 0

Если p~ > 0, то

i=1

j=1

− i=1

Неравенство p~ ~xi 6 p~ w~i

+ αijπ˜j(p~ ) превращается в равенство

Задача. Доказать это.

p~ = p~ w~ +

P P

α π˜ (p~ ) = p~ w~ + (p~ ) = p~ w~ + p~ ~y

i=1

i=1 j=1

i=1

j=1

i=1

j=1

Лемма (Закон Вальраса в широком смысле). Пусть ~u χ(p~), где p~ > 0, p~ 6= 0, то p~u > 0

Задача. Доказать лемму.

Лемма (Гейл–Никайдо–Дебре). Пусть S = {(p1, ..., pl) > 0| P ps = 1}, χ: S → 2 , где –

s=1

выпуклый компакт в Rl. Если

1)p~ S χ(p~) – непустое выпуклое множество;

2)χ – замкнутое отображение;

3) p~ S, u χ(p~)				p~u > 0
Тогда	p~	S: χ(p~ )		l	=
			∩ R+		6
Доказательство. Вспомним точечное отображение :
p~ S, ~u ставится в соответствие вектор из S
				θi(p,~ ~u) =		pi + max(0, −ui)		, i = 1, ..., l	(3.11)
							l
						sP
						1 +	=1 max(0, −us)

θi = 1, т.к. pi = 1

θ : S × → S непрерывно и однозначно.
~	×	χ: S	×	→	2S×
Декартово произведение θ~

(θ(p,~ ~u), χ(p~)) S ×

~ × : × → S× непустое выпуклое отображение,

θ χ S 2

~× – замкнутое отображение,

θχ

S × – выпуклый компакт по теореме Какутани существует неподвижная точка p~ S,

: ~ , (3.11) примет вид :

~u θ(p~ , ~u ) = p~ ~u χ(p~ )

+ max(0,

u )

− i

= pi

1 +

=1 max(0, −us)

u ) = max(0,

u )

max(0,

(3.12)

− s

− i

s=1

Умножим (3.12) на ui и просуммируем :

max(0,

u ) =

u ))2

p~ ~u

u ) =

u max(0,

−

(max(0,

s=1

− s

− i

i=1

max(0, −ui ) = 0 ui > 0 i = 1, ..., l ~u > 0 χ(p~ ) ∩ Rl+ 6=

Задача. Доказать 2).

Пример (Эрроу). l = 2, m = 2, n = 1, Y = {0}

u1(x1, x2) = x1, w~(1) = (1, 1),

u2(x1, x2) = x1 + x2, w~(2) = (0, 1). Конкурентное равновесие не существует. Пусть существуют равновесные цены p1 и p2.

p2 = 0 неограниченный спрос на второй товар у второго потребителя, а его запас ограничен равновесия не существует.

Теорема (Первая теорема теории благосостояния). Пусть {p~ , ~x1, ..., ~xm, ~y1 , ..., ~yn} – конкурентное равновесие. Тогда оно оптимально по Паретто, т.е.

6 ~x1, ..., ~xm, ~y1, ..., vyn :

1)	~yj	Yj j = 1, ..., n
2)	m			n	m
2)	iP	w~(i) + ~yj > xi
	iP			P	P
	=1			j=1	i=1
3)	u (~x )		>	u (~x ) (i = 1, ..., m)		u	i0	(~x ) > u	i0	(~x )
	i	i	>	i i			i0	i	i0	i

Задача. Доказать эту теорему.

<<< < Предыдущая 1 2 3 4 56 / 66

Соседние файлы в папке ЭКОНОМЕТРИКА и математическая экономика

#
20.04.2015151.4 Кб76Моисеев С.Р. Аналитика центральных банков. Обзор эконометрических моделей. 2003.pdf
#
20.04.201529.59 Mб77Мур Дж. и др. Экономическое моделирование в Microsoft Excel. 2004.djvu
#
20.04.201511.63 Mб97Орлова И.В. Экономико-мататематические методы и модели. Выполнение расчетов в среде Excel. 2000.pdf
#
20.04.2015578.01 Кб73Солопахо А.В. Математика в экономике (ТамбовГТУ).pdf
#
20.04.20151.91 Mб170Тихонов Э.Е. Методы прогнозирования в условиях рынка.pdf
#
20.04.2015467.72 Кб176Шананин А.А. Математические модели в экономике. 1999.pdf
#
20.04.20153.81 Mб77Эконометрика. Под.ред. И.И.Елисеевой. 2003.djvu
#
20.04.20154.02 Mб512Эконометрика. Учебник продвинутый (2005).pdf