Иллюстративный материал к Лекции 1

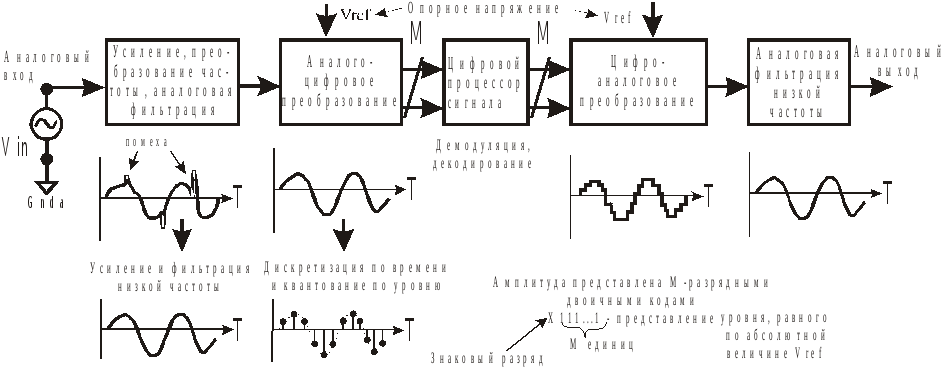
Примеры аналоговых операций над сигналом с

применением Операционных Усилителей (ОУ)

Активный RC интегратор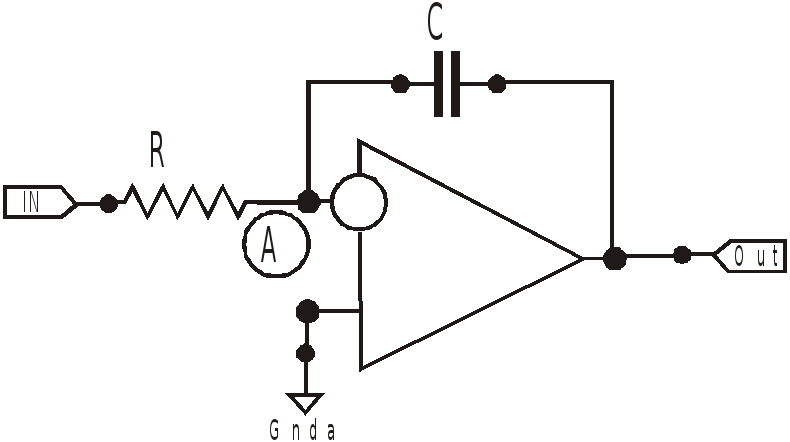

В S-области: - передаточная функция активного RC интегратора

Пассивная RC интегрирующая цепочка

Определим модуль и фазу передаточной функции (ПФ). Для этого переменная s заменяется на jω:

tg(φ)=ωRC

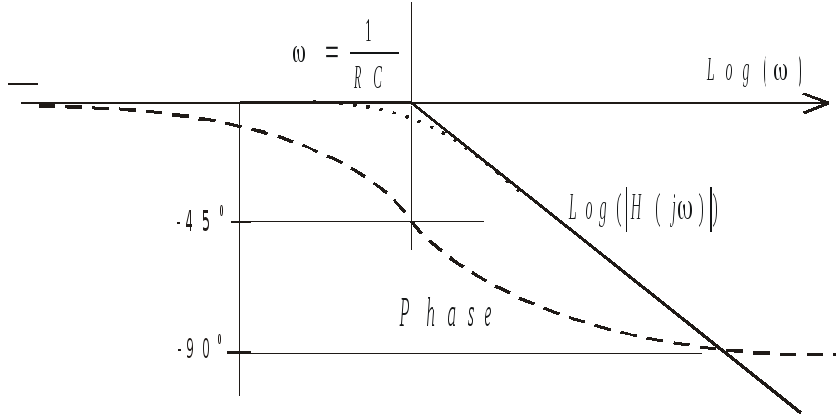
При анализе модуль ПФ аппроксимируют асимптотами. Принимают, что для - , а для - модуль ПФ уменьшается обратно пропорционально частоте. Для точных оценок имеют в виду, что при модуль равен или -3 дБ.

А

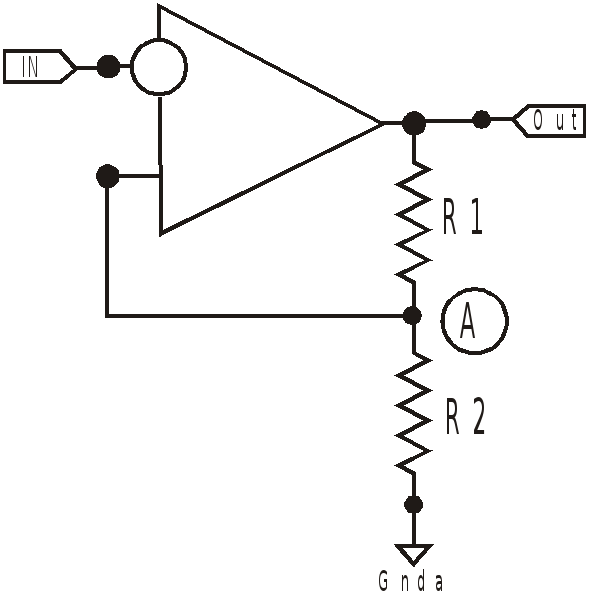
Неинвертирующий

усилитель

Инвертирующий

усилитель

налогично находится модуль и фаза ПФ для активного RC интегратора При идеальном ОУ: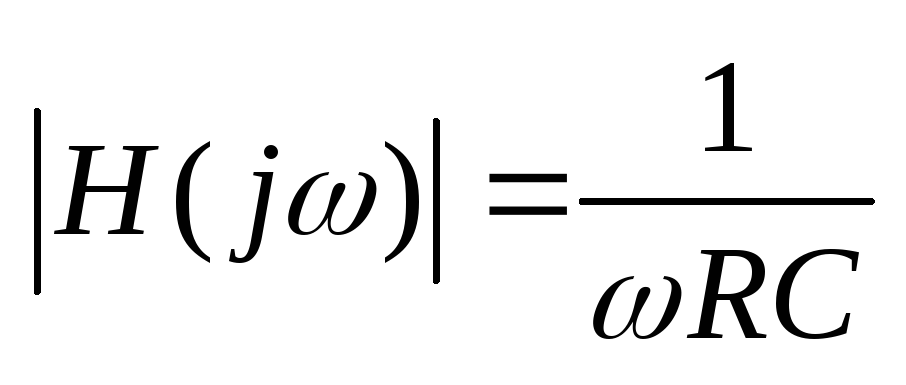; Фаза равна -90^О. При неидеальном ОУ. пусть его усиление равно К_О. Имеем уравнения: (1).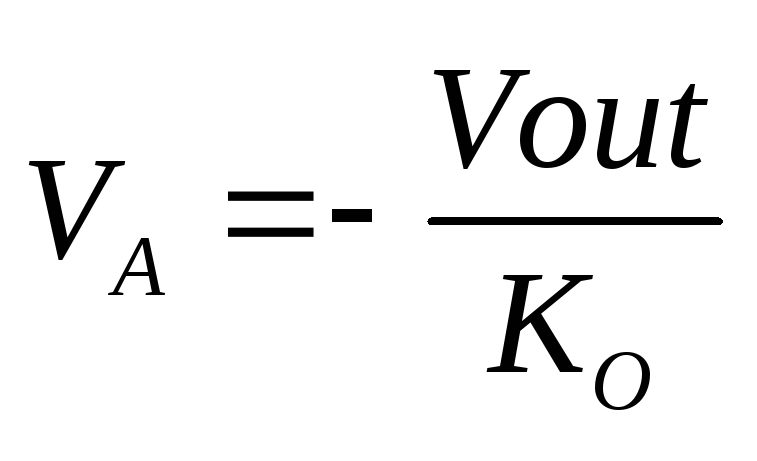; (2).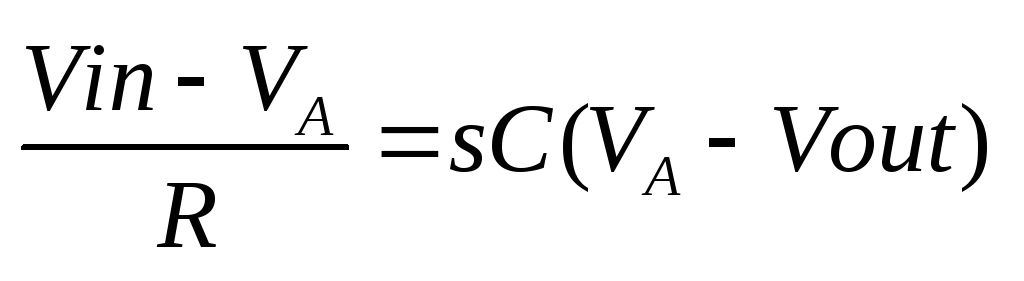. Решением является:

Для полагают, что при усиление интегратора (т.е. модуль ПФ) равен , а для - модуль ПФ уменьшается обратно пропорционально частоте

ВВЕДЕНИЕ В АКТИВНЫЕ RC ФИЛЬТРЫ (ARC ФИЛЬТРЫ)

Известно, что ПФ фильтра в общем выражается отношением полиномов: (1-1) где, как правило, . При действительных коэффициентах корни полиномов могут быть либо действительными, либо комплексно–сопряженными, поэтому одним из способов реализации фильтра является разложение на произведение М простых дробей, в которых числители и знаменатели являются полиномами не выше второго порядка: (1-2). Как интерпретировать такой вид ПФ? Рассмотрим систему, в которой друг за другом включены М подсистем, так что выход предыдущей является входом последующей. Тогда ПФ системы равна:

(1-2) Из выражения очевидно, что если ПФ всей системы равна произведению всех ПФ всех подсистем, то подсистемы включены последовательно друг за другом. Итак, необходимо уметь реализовать подсистему фильтра, описываемого рациональной дробью с числителем и знаменателем 2 – го порядка. Такой фильтр называется биквадом.

Имеем ПФ биквада: 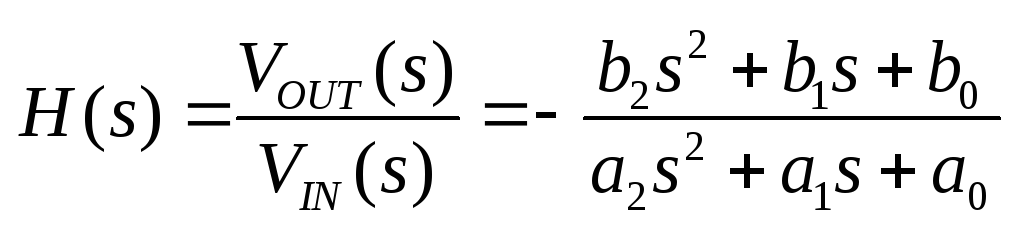. (1-3). Знак «минус» перед дробью не играет принципиальной роли, но с ним реализация получается проще. Итак, имеем:

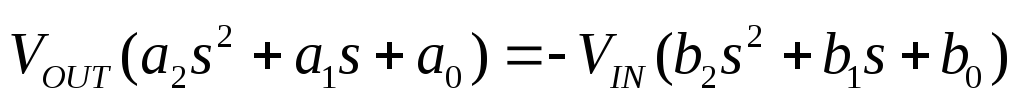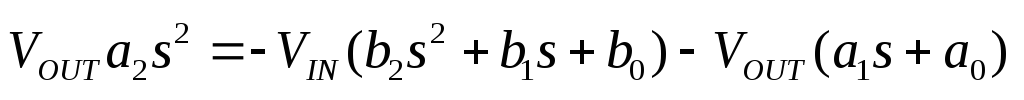или ;

, или

(1-4)

Элемент подразумевает применение активного RC интегратора; элемент типа является параллельным соединением резистора и конденсатора; элемент типа является проводимостью, т.е обратным резистором. Об этом - в следующей лекции.