2.3. Организация ветвлений

Очень распространенной задачей является программирование процессов с несколькими исходами – ветвящихся процессов.

Задача 1. Для произвольного аргумента Х вычислить значение кусочно-ломаной функции Y(X) (рис. 2.3.1).

5+X при Х<0

Y = 5 при 0<=Х<10

10–0,5X при X>=10

Одно из возможных решений задачи приведено на рис.2.3.2 и 2.3.3. Здесь имена переменных отображены строчными буквами, а ключевые слова – прописными только для наглядности. Как уже указывалось, регистр букв безразличен – в Бейсике они воспринимаются одинаково.

Программа к задаче 1

Input “Укажите х”, X

IF x<0 THEN y=5+x: GOTO 2

IF x<10 THEN y=5: GOTO 2

y=10–0.5*x

2 PRINT y

END

Рис. 2.3.2

Здесь используется помеченный оператор (2 PRINT y). Необходимость в этом возникла вследствие потребности перейти к печати от операторов IF, минуя оператор y=10-0.5*x. В данном случае метка может быть любым числом, а не только 2. Замечание. В блок-схеме на связях имеющих очевидное направление стрелки можно не указывать.

Следует отметить, что практически любая задача может быть запрограммирована различными способами. Например, здесь возможно и такое решение.

INPUT x

IF x<0 THEN y=5+x: PRINT y: END

IF x<10 THEN y=5: PRINT y: END

y=10-0.5*x: PRINT y

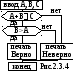
Задача 2. Даны три произвольных числа А, В, С. Составить программу, которая анализирует их и, если сумма первых двух чисел не меньше третьего, а второе число больше первого – выдает сообщение ВЕРНО. Если хотя бы одно из условий не выполняется – то сообщение НЕВЕРНО. Иными словами

“ВЕРНО” если А+В>=C и В>A

“НЕВЕРНО” – в противном случае

На рис. 2.3.4 и 2.3.5 представлено решение (блок-схема и программа), полностью адекватное условию. Однако в некоторых случаях решение удобно искать, преобразовав условие на обратное, т.е.

“НЕВЕРНО” если А+В<C или В<=A

“ВЕРНО” – в противном случае

Это позволяет иногда упростить программирование. Программа для этого случая приведена на рис. 2.3.6.

Программы к задаче 2.

INPUT a,b,c INPUT a,b,c

IF a+b>=c GOTO 7 IF a+b<c GOTO 15

? “Неверно”: END IF b<=a GOTO 15

7 IF b>a THEN ? “Верно” ? “Верно”: END

15 ? “Неверно”

Рис. 2.3.5 Рис. 2.3.6

ЛОГИЧЕСКИЕ ФУНКЦИИ. При необходимости выполнять анализ одновременно нескольких условий удобно воспользоваться логическими функциями. Аргументами логических функций являются высказывания, в отношении которых всегда можно сказать истинны они или ложны. К таким высказываниям относятся математические операции сравнения – равно, больше, меньше и т.д. Так, например, выражение вида Х=Y всегда может быть только истинным или только ложным. Программисту доступны следующие шесть логических операций (таблица 2.3.1):

Функция	Название	Определение
NOT	Отрицание НЕ	Выражение NOT Aистинно тогда и только тогда, когда А ложно
AND	Логическое умножение И	A AND Bистинно тогда и только тогда, когда истинно и А и истинно В
OR	Логическое сложение ИЛИ	A OR Bистинно тогда и только тогда, когда хотя бы одно из А и В истинно
XOR	Исключающее ИЛИ	A XOR Bистинно тогда и только тогда, когда значения аргументов не совпадают
EQV	Эквивален- тность	A EQV Bистинно тогда и только тогда, когда оба аргументы истинны или оба ложны
IMP	Импликация	A IMP Bпринимает значение ложь, если А истинно, а В ложно, и истина в других случаях

Таблица 2.3.1

Важнейшими для нас являются функции И, ИЛИ, НЕ, которые образует так называемый основной полный набор логических функций, т.е. только с их помощью (без привлечения других элементарных логических функций) можно описать какие угодно сложные логические зависимости. Остановимся на них подробнее. Функция НЕ (NOT) – является функцией одного аргумента. Другие названия функции НЕ – функция инверсии, поскольку ее значение всегда обратно аргументу. Поведение функции описывает таблица 2.3.2. Например, следующие два оператора полностью идентичны

IF X<10 THEN Y=5 IF NOT X>=10 THEN Y=5

Поведение логических функций И, ИЛИ описывает таблица 2.3.3. Эти функции требуют двух аргументов. Функция И (AND) истинна тогда и только тогда, когда истинны все ее аргументы. Функция ИЛИ (OR) истинна тогда, когда истинен хотя бы один из ее аргументов. Если нет скобок, функции вычисляются в следующей последовательности: НЕ, И, ИЛИ.

В качестве примера снова рассмотрим задачу 2 в исходной формулировке. Теперь ее решение сводится практически к одной строке и приведено ниже.

INPUT a,b,c

IF a+b>=c AND b^2>a THEN ? “Верно” ELSE ? “Неверно”

Аргумент	Функция НЕ		Первый аргумент	Второй аргумент	Функция И	Функция ИЛИ
Ложь	Истина		Ложь	Ложь	Ложь	Ложь
Истина	Ложь		Ложь	Истина	Ложь	Истина
			Истина	Ложь	Ложь	Истина
			Истина	Истина	Истина	Истина
Таблица 2.3.2				Таблица	2.3.3

Другой пример. Для произвольных чисел А, В, С выяснить, правда ли что первое число самое большое, а последнее – самое маленькое.

IF a>b AND a>c AND c<a AND c<b

THEN ? “Верно” ELSE ? “Неверно”

Еще. Правда ли, что среди чисел А, В, С имеется ровно одна единица.

IF (a=1 AND b<>1 AND c<>1) OR

(a<>1 AND b=1 AND c<>1) OR

(a<>1 AND b<>1 AND c=1)

THEN ? “Верно” ELSE ? “Неверно”

Здесь скобки введены только для наглядности поскольку операция AND все равно выполняется прежде операции OR.

 Тест. 2.3.1. Укажите результат, выдаваемый программой 1). 1, 2) 2.

x=2: y=4: z=3

if x>y or y>z then print 1 else print 2

 Контрольная задача. В устройстве ввода ЭВМ подготовлено четыре произвольных числа: A,B,C,D. ЭВМ должна ответить на вопрос: Правда ли что ...? (вопрос берется из таблицы). Ответ ЭВМ должна вывести в виде текста: слова ”Правда” или ”Неправда”. Составить блок-схему, программы. Сделать проверку для произвольных аргументов.

Вопрос

Все числа положительны?

Ни одно из чисел не превышает число 90?

Каждое из первых двух чисел больше каждого из последних двух?

Первое число меньше остальных?

Эти числа расположены в возрастающей последовательности?

Эти числа расположены в убывающей последовательности?

Среди этих чисел есть равные?

Среди этих чисел нет равных?

Первое число не самое маленькое?

Все четыре числа равны между собой?