4.1. Линейная регрессия

Самый простой и популярной является аппроксимация прямой линией – линейная регрессия.

Пусть мы имеем фактическую информацию об уровнях прибыли Y в зависимости от размера X капиталовложений – Y(X). На рис. 4.1-1 показаны четыре такие точки М(Y,X). Пусть также у нас имеются основания предполагать, что зависимость эта линейная, т.е. имеет вид Y=А+ВX. Если бы нам удалось найти коэффициенты A и B и по ним построить прямую (например, такую, как на рисунке), в дальнейшем мы могли бы сделать осознанные предположения о динамике бизнеса и возможном коммерческом состоянии предприятия в будущем. Нас бы устроила прямая, находящаяся как можно ближе к известным точкам М(Y,X), т.е. имеющая минимальную сумму отклонений или сумму ошибок (на рисунке отклонения показаны пунктирами). Известно, что существует только одна такая прямая. Для решения этой задачи используют метод наименьших квадратов ошибок. Разность (ошибка) между известным значением Y₁ точки М₁(Y₁,X₁) и значением Y(X₁), вычисленным по уравнению прямой для того же значения X₁, составит

₁ = Y₁ – A – B•X₁.

Такая же разность

для X=X₂ составит ₂ = Y₂ – A – B•X₂;

для X=X₃ ₃ = Y₃ – A – B•X₃;

и для X=X₄ ₄ = Y₄ – A – B•X₄.

Запишем выражение для суммы квадратов этих ошибок

Ф(A,В)=(Y1–A–B•X1)²+(Y2–A–B•X2)²+(Y3–A–B•X3)²+(Y4–A–B•X4)²

4

или сокращенно Ф(B,A)=(Yi – A – BXi)².

i=1

Здесь нам известны все X и Y и неизвестны коэффициенты A и B. Проведем искомую прямую так (т.е. выберем A и B такими), чтобы эта сумма квадратов ошибок Ф(A,B) была минимальной. Условиями минимальности являются известные соотношения

Ф(A,B)/A=0 и Ф(A,B)/B=0.

Выведем эти выражения (индексы при знаке суммы опускаем):

[(Yi–A–B•Xi)²]/A =(Yi–A–B•Xi)(–1)

[(Yi–A–B•Xi)²]/B =(Yi–A–B•Xi)(–Xi).

Преобразуем полученные формулы и приравняем их нулю

2(–Yi +B•Xi +A) = 0

2(–Xi•Yi +B•Xi² +A•Xi) = 0.

Сократим выражения на 2 и раскроем скобки. Тогда

–Yi + BXi + A= 0

–Xi•Yi+BXi²+AXi= 0.

Мы получили систему из двух линейных алгебраических уравнений, в которой неизвестными являются A и B, а сумма N единиц равна N (в нашем случае 1=4). Перенесем свободные члены в правую часть и для упрощения записи опустим индексы при знаке суммирования. Окончательно получим:

B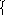X+NA=Y

BX²+AX=XY.

Решив эту систему с помощью любого известного метода линейной алгебры, получим

В=(N•XY–X•Y)/( N•X²–X•X), А=(N•X²–X•X)/(N•X²–X•X).

В случае, если величина Y зависит не от одного, а от нескольких параметров Y(x,z, ...w), задача нахождения коэффициентов решается аналогично и называется задачей множественной регрессии.

Оценить функциональную близость (в линейном смысле) значений Х и Y можно с помощью коэффициента корреляции R, который находится по следующей формуле

R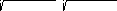=(N•XY –X•Y)/( N•X²–X•X•N•Y²–Y•Y ).

Cчитается что при R0,3 наблюдается слабая линейная связь, при R= 0,30,7 – средняя, при R0,7 – сильная, при R0,9 – весьма сильная связь, при R=1 – полная функциональная связь (все точкиY(X) лежат на одной прямой).

В Excel имеются функции для нахождения коэффициентов уравнения линейной регрессии.

 ЛИНЕЙН(известное Y; известное X)– вычисляет два коэффициента линейного уравнения регрессии для множества значений независимой переменной Х и зависимой переменной Y. Результат выводится в две смежные ячейки – сначала коэффициент при Х, затем – свободный член. Функция должна вводиться как функция обработки массива: выделяются две ячейки для результата, вводится функция и нажимаются клавиши Ctrl+Shift+Enter (вместо обычного Enter).

Пример. Если исходные данные расположены, как показано на рис. 4.1-2, и в C3:D3 введена функция {=ЛИНЕЙН(B2:B11;A1:A11)}, резуль­таты в C3 и D3 можно интерпретировать как коэффициенты линейного уравнения регрессии y=0,6364x+1,8. Таким образом, если нам понадобится вычислить ожидаемое значение прибыли Y в будущем, например, при капитало­вложениях в сумме 20 единиц, нужно подставить их в найденную функцию Y=0,64+1,8*20=36,64.

 ТЕНДЕНЦИЯ(известное Y; известное X; новое X) – вычисляет ожидае­мое новое значение Y для нового Х, если известны некоторые опытные значения X и Y и в предположении, что Х и Y зависят линейно.

	А	В	С	D
1	Х	Y
2	1	1	ЛИНЕЙН
3	2	5	0,64	1,8
4	3	6
5	4	5
6	5	4	ТЕНДЕНЦИЯ
7	6	3	12	9,44
8	7	4	4,5	4,66
9	8	6
10	9	9
11	10	10	Ри	с.4.1.2

Пример: Исходные данные расположены (рис. 4.1-2) вC7 иC8, результаты – в

D7=ТЕНДЕНЦИЯ(B2:B11;A1:A11;G4) и

D8=ТЕНДЕНЦИЯ( B2:B11; A1:A11;G5).

Таким образом, при Х=12 ожидается Y=9,44, а при Х=4,5; Y=4,66.

Используя значения X и Y с помощью Excel, построим график, совмещенный с линией регрессии (линией тренда), как показано на рис.4.1.3.

 В Excel имеется очень простой способ строить линейную аппрокси­ма­цию равноотстоящих значений аргумента. Для этого нужно выделить известные значения прогнозируемой величины и потянуть за маркер запол­нения, удерживая правую кнопку мыши. Затем, из появившегося контекстного меню выбрать пункт Линейное приближение. В заполняе­мых клетках мы обнаружим значения, вычисленные системой для самостоятельно найденного ею линейного уравнения регрессии. На рис.4.1.4 исходными значениями являются 2, 4, 5. Остальные числа являются вычисленным прогнозом в предположении линейной связи аргументов в соответствии с найденным Excel уравнением. Здесь же (рис.10.1.5), при необходимости, можно выбрать и Экспо­ненциальное приближение.

2	4	5	6,67	8,17	9,67	11,17	12,67	Рис. 4.1.4
2	4	5	8,55	13,52	21,37	33,80	53,44	Рис. 4.1.5

Спомощью средств деловой графикиExcel можно не только построить необходимые кривые, но получить линии тренда и соответствующие им уравнения Y(X) (здесь y=1,5x+0,6667 для линейного закона, y=1,368e^0,4581x – для экспоненты). Экспоненциальная аппроксимация обозначена прямоугольными точками, линейная – кружками. Исходные точки обведены овалом.