3.2. Численное интегрирование функций

Известные методы численного нахождения определенного интеграла Sв диапазоне от Хн до Хк

Xкn-1

S=_Y(x)dxSпрxY_i(метод прямоугольников)

Хнi=0

легко реализуются в Excel (рис.3.2а).

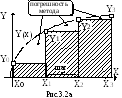
Определенный интеграл функции Y(X) пропорционален площади под кривой. Простейший способ ее нахождения – метод прямоугольников.

	A	B	C	D	E
1		0,1
2	Хн=	0		М е т о д:
3	Шаг	X	f(x)	пря- моуг.	трапе- ций
4	1	0,0	0	0	0
5	2	0,1	0,01	0,000	0,001
6	3	0,2	0,04	0,001	0,003
7	4	0,3	0,09	0,005	0,010
8	5	0,4	0,16	0,014	0,022
9	6	0,5	0,25	0,030	0,043
10	7	0,6	0,36	0,055	0,073
11	8	0,7	0,49	0,091	0,116
12	9	0,8	0,64	0,140	0,172
13	10	0,9	0,81	0,204	0,245
14	11	1,0	1,00	0,285	0,335
			Рис	.3.2в

Если разбить диапазон интегрирования на отрезки с равным шагом x, то суммаSпр площадей прямоугольников, построен­ных на этих отрезках с высотой, равной ординате в начальной точке отрезка, даст приближенное значение искомого интеграла (заштриховано). Из рисунка видно, что вычисления могут сопровождаться значи­тельными ошибками – между верхней площадкой прямоугольника и кривой остается неучтенный сегмент. Для снижения погрешности следует умень­шить шаг интегрирования, либо использовать более точные методы. Таким методом является, также весьма простой, метод трапеций (рис. 3.2б). Здесь элементарной площадкой является трапеция. Площадь такой фигуры определяется как средняя сумма ординат на ее краях, умноженная на ширину основания (ширину шага). Таким образом

SтрX• [(X₀+X₁)/2+(X₁+X₂)/2+(X₂+X₃)/2+ ...(X_n-1+X_n)/2]

n-1

или Sтр x Y_i+Y_i+1)/2.

i=0

	A	B	C	D	E
1	Х=	0,1
2	Хн=	0		М е	т о д:
3	Шаг	X	Y(x)	прямоуг.	трапеций
4	1	0,00	=B4^2	0	0
5	=A4+1	=B4+B$1	=B5^2	=D4+C4*B$1	=E4+(C4+C5)*B$1/2
6	=A5+1	=B5+B$1	=B6^2	=D5+C5*B$1	=E5+(C5+C6)*B$1/2
				Рис.3.2г

На рис.3.2в приведено решение методами прямоугольников и трапеций для функции Y=X², а на рис.3.2г – используемые формулы. Шаг интегрирования и нижний предел интегрирования занесены в клетки В1 и В2. В столбце А формируется номер шага, а в столбце В – очередное значение независимой переменной Х. В столбце С вычисляется текущее значение подинтегральной функции Y(X), в столбцах D и Е накапливаются результаты интегрирования. На рис.3.2в интегрирование с шагом 0,1 доведено до X=1. При необходимости расширить диапазон интегрирования следует скопировать вниз последнюю строку таблицы до достижения желаемого значения верхнего предела интегрирования (Х). Шаг интегрирования может быть изменен непосредственно в ячейке В1. Формульное представление фрагмента таблицы – на рис.3.2г.

С целью проверки результатов можно вычислить определенный интеграл вручную. Видим, что результат, полученный методом трапеций, уже весьма близок к точному.

1 1

S = _Х²dx= Х³/3 = 1/3=0,333.

_{0 0}

Замечание. Сравните с решением той же задачи путем программирования.

 Тест. 3.2.1. Почему прибегают к численному интегрированию функций вместо аналитического? 1). это делается быстрее, 2). аналитическое решение не всегда возможно, 3) повышается точность решения.