Вторая теорема двойственности

Пусть имеется симметричная пара двойственных задач

, , , .

, , .

Теорема 4. Для того чтобы допустимые решения ,являлись оптимальными решениями пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие равенства:

;

.

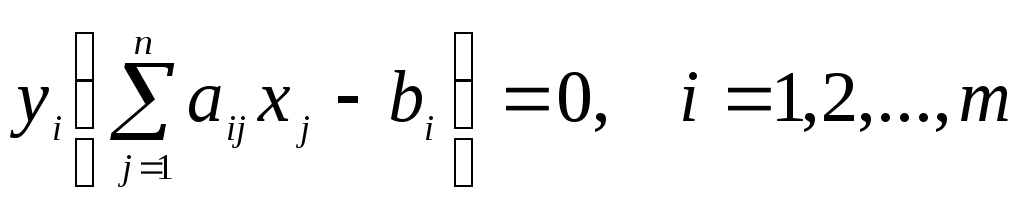Иначе, если при подстановке оптимального решения в систему ограничений ограничение исходной задачи выполняется как строгое неравенство, токоордината оптимального решения двойственной задачи равна нулю, и, наоборот, есликоордината оптимального решения двойственной задачи отлична от нуля, тоограничение исходной задачи удовлетворяется оптимальным решением как равенство.

Пример.

Исходная задача	Двойственная задача
При ограничениях	При ограничениях

Решая исходную задачу графическим методом, получим , при этом.

По 2-ой теореме двойственности систему ограничений двойственной задачи можно записать в виде равенств:

Подставим в систему ограничений исходной задачи:

Тогда система ограничений двойственной задачи примет вид

Откуда . При этом.

Пусть дано решение двойственной задачи ,, найдем решение исходной. По 1-ой теореме двойственности . Так как , то по 2-ой теореме двойственности второе и третье неравенства исходной задачи обращаются в равенства;

Откуда , при этом .

§1.5 Транспортная задача линейного программирования.

1. Математическая модель.

Однородный груз сосредоточен у m поставщиков в объемах . Данный груз необходимо доставить n потребителям в объемах . Известны () – стоимости перевозки единицы груза от каждого i-го поставщика каждому j-му потребителю. Требуется составить такой план перевозок, при котором запасы всех поставщиков вывозятся полностью, запросы всех потребителей удовлетворяются полностью и суммарные затраты на перевозку всех грузов минимальны.

Исходные данные транспортной задачи записываются в таблице вида

			…
			…
…	…	…	…	…
			…

Переменными (неизвестными) транспортной задачи являются () – объемы перевозок от каждого i-го поставщика каждому j-му потребителю. Эти переменные могут быть записаны в виде матрицы перевозок

.

Математическая модель транспортной задачи в общем случае имеет вид.

, (1)

, (2)

(3)

, . (4)

Целевая функция задачи выражает требование обеспечить минимум суммарных затрат на перевозку всех грузов. Равенство (2) из m уравнений описывает тот факт, что запасы всех m поставщиков вывозятся полностью. Вторая группа из n уравнений в равенстве (3) выражает требование полностью удовлетворить запросы всех n потребителей. Неравенство (4) является условием неотрицательности всех переменных задачи.

Т.о. математическая формулировка транспортной задачи состоит в следующем: найти переменные задачи , , удовлетворяющие системам ограничений , , условиям неотрицательности и обеспечивающие минимум целевой функции .

В рассмотренной модели транспортной задачи предполагается, что суммарные запасы поставщиков равны суммарным запросам потребителей, т.е. . Такая задача называется задачей с правильным балансом, а ее модель – закрытой. Если же это равенство не выполняется, то задача называется задачей с неправильным балансом, а ее модель – открытой.

Для того чтобы транспортная задача линейного программирования имела решение, необходимо и достаточно, чтобы суммарные запасы поставщиков равнялись суммарным запросам потребителей, т.е. задача должна быть с правильным балансом.

Пример. Составить математическую модель транспортной задачи. Исходные данные которой представлены в таблице.

	50	70	80
90	9	5	3
110	4	6	8

Решение.

Введем переменные задачи (матрицу перевозок)

.

Запишем матрицу стоимостей

.

Целевая функция задачи:

Данная функция, определяющая суммарные затраты на все перевозки, должна достигать минимального значения.

Составим систему ограничений. Сумма перевозок, стоящих в первой строке матрицы Х, должна равняться запасам первого поставщика, а сумма перевозок во второй строке матрицы Х – запасам второго поставщика:

.

Это означает, что все запасы поставщиков вывозятся полностью.

Суммы перевозок, стоящих в каждом столбце матрицы Х, должны быть равны запросам соответствующих потребителей:

Это означает, что запросы потребителей удовлетворяются полностью. Необходимо также учитывать, что перевозки не могут быть отрицательными.

Ответ: математическая модель задачи формулируется следующим образом: найти переменные задачи, обеспечивающие минимум функции

и удовлетворяющие условию системе ограничений

и условиям неотрицательности , .