§5.2 Решение игр в смешанных стратегиях.

Если игра не имеет седловой, то применение чистых стратегий не дает оптимального решения игры. В таком случае можно получить оптимальное решение, случайным образом чередуя чистые стратегии.

Смешанной тратегией игрока А называется применение чистых стратегий с вероятностями , причем сума вероятностей равна единицы. Смешаные стратегии игрока А записываются в виде матрицы

или в виде строки . Аналогично смешанные стратегии игрока B обозначаются

или , где .

Чистые стратегии можно считать частным случаем смешанных и задавать строкой, в которой единица соответствует чистой стратегии. На основании принципа минимакса определяется оптимальное решение. Цена игры удовлетворяет неравенству

,

где β – нижняя и верхняя цены игры.

Основная теорема теории игр – теорема Неймана. Каждая конечная игра имеет по крайней мере одно оптимальное решение, возможно, среди смешанных стратегий.

Пусть и – пара оптимальных стратегий. Если чистая стратегия входит в оптимальную смешанную стратегию с отличной от нуля вероятностью, то она называется активной.

Теорема 6 (об активных стратегиях). Если один из игроков придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры , если второй игрок не выходит за пределы своих активных стратегий.

Игра размера 2 х 2 является простейшим случаем конечной игры. Если такая игра имеет седловую точку, то оптимальное решение – это пара чистых стратегий, соответствующих этой точке.

В игре, в которой отсутствует седловая точка, в соответсвии с основной теоремой игр оптимальное решение существует и определяется парой смешанных стратегий и .

Для того чтобы их найти, воспользуемся теоремой об активных стратегиях. Если игрок A придерживается своей оптимальной стратегии , то его средний выигрыш будет равен цене игры , какой бы активной стратегией ни пользовался игрок B. Для игры 22 любая чистая стратегия противника является активной, если отсутствует седловая точка. Выигрыш игрока A (проигрыш игрока B) – случайная величина, математическое ожидание (среднее значение) которой является ценой игры. Поэтому средний выигрыш игрока A (оптимальная стратегия) будет равен и для первой, и для второй стратегии противника.

Пусть игра задана платежной матрицей

,

а игроки A и B используют оптимальные смешанные стратегии

; .

Эти стратегии и цена игры определяются из систем уравнений

решения которых

, ,

, ,

.

Пример. Найти оптимальные стратегии игры, заданной платежной матрицей .

Решение. Т.к. , , поэтоиу решение ищем в смешанных стратегиях. Для игрока А стредний выйгрыш равен цене игры v (при ). Для игрока В средний проигрыш равен цене игры v (при ). Системы уравнений, записанные ранее, в этом случае имеют вид

.

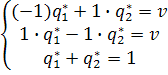Решая эти системы, получаем , .

Это означает, что оптимальная стратегия каждого игрока состоит в том, чтобы чередовать свои чистые стратегии случайным образом, при этом средний выйгрыш равен 0.

Пусть игра m x n , без седловой точки задана платежной матрицей , i = 1, 2, … , m; j = 1, 2, … , n. Игрок A обладает стратегиями , , … , , а игрок B – стратегиями , , … , . Необходимо определить оптимальные стратегии и

Цель игрока A (B) – максимизировать (минимизировать) гарантированный выигрыш (проигрыш), т.е. цену игры ν, или минимизировать (максимизировать) величину 1/ν.

При такой постановке оптимальной стратегии и определяются как решения двух взаимно двойственных задач линейного программирования:

при ограничениях

, , … , ,

где ,

при ограничениях

, , … , ,

где .

При этом цена игры

.

Пример. Предприятие может выпускать три вида продукции , получая при этом прибыль, зависящую от спроса, который может быть в одном из четырех состояний . Дана матрица, ее элементы характеризует прибыль, которую получит предприятие при выпуске i-й продукуции с j-м состоянием спроса.

	3	3	6	8
	9	10	4	2
	7	7	5	4

Определить оптимальные пропорции в выпускаемой продукции, гарантирующие среднюю величину прибыли при любом состоянии спроса, считая его неопределенным.

Решение. Задача сводится к игровой модели, в которой игра предприятия A против спроса B задана платежной матрицей. Прежде чем решать задачу, можно попытаться упростить игру, проведя анализ платежной матрицы и отбросив стратегии, заведомо невыгодные или дублирующие. Так, вторая стратегия (второй столбец матрицы) является явно невыгодной для игрока B по сравнению с первой (элементы второго столбца не меньше элементов первого столбца), так как цель игрока B – уменьшить выигрыш игрока A. Поэтому второй столбец можно отбросить. Получим матрицу P размера 3 х 3:

.

спрос вид продукции
	3	6	8	3
	9	4	2	2
	7	5	4	4
	9	6	8	4 6

Определим нижнюю и верхнюю цены игры в таблице.

Так как , то седловая точка отсутствует и оптимальное решение следует искать в смешанных стратегиях игроков:

и .

Обозначим , i = 1, 2, 3 и , j = 1, 2, 3, составим две взаимно двойственные задачи линейного программирования.

Задача 1

, i = 1, 2, 3

.

Задача 2

, j = 1, 2, 3

.

Решая каждую задачу симплексным методом, получаем

при оптимальном базисном решении

Из соотношений находим цену игры

.

По формулам ,

;

, т.е.

.

Итак, предприятие должно выпустить 40% продукции и 60% продукции , а продукцию не выпускать.

;

;

, т.е.

.

(учтено исключение второго столбца исходной матрицы).

Итак, оптимальный спрос в 20% случаев находится в состоянии и 80% – в состоянии .