-Федеральное агентство по образованию

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ТЕХНОЛОГИЙ И УПРАВЛЕНИЯ

(образован в 1953 году)

Кафедра высшей математики

А.А.Копанева, А.В.Овсянникова, И.Ф.Авдеев

МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ЭКОНОМИКЕ

Учебно-методическое пособие для студентов специальностей 080105 (0604), 080109 (0605) 080102 (0606), 080502 (0608),080507 (0611), всех форм обучения

www.mgutm.ru

2010г.

Москва 2009

УДК

 А.А.Копанева, А.В. Овсянникова, И.Ф.Авдеев Математические методы в экономике. Учебно-методическое пособие для студентов экономических специальностей.- М.: МГУТУ, 2009.

Данное учебно-методическое пособие включает программу по высшей математике 2 курса четвертого семестра для студентов дневной формы обучения. Содержит теоретические сведения, разобранные примеры задач и список рекомендуемой литературы. Может быть использовано для студентов всех форм обучения и аспирантов, а также исследователями в различных областях науки, применяющими математические методы при решении экономических задач.

Авторы: А.А.Копанева, А.В. Овсянникова, И.Ф.Авдеев

Рецензент: д.ф.-м.н., Зуев Ю.А.

Редактор: Свешникова Н.И.

Московский государственный университет технологий и управления, 2009

109004, Москва, Земляной вал, 73

Содержание

Тема 1 Линейное и целочисленное программирование……………………….4

§1.1 Общая постановка задачи линейного программирования. Классические задачи…………………………………………………………………………………4

§1.2 Решение задач линейного программирования графическим методом……...7

§1.3 Симплекс-метод. Метод искусственного базиса……………………………..9

§1.4 Двойственные задачи…………………………………………………………15

§1.5 Транспортная задача линейного программирования……………………….18

§1.6 Целочисленные задачи линейного программирования. Метод Гомори…..27

Тема 2 Задачи нелинейной оптимизации и динамического программирования………………………………………………………………..33

§2.1 Понятие о параметрическом и стохастическом программировании………33

§2.2 Динамическое программирование. Принцип оптимальности Беллмана….34

Тема 3 Сетевые методы в экономике…………………………………………..37

§3.1 Сетевая модель и ее основные элементы……………………………………37

§3.2 Временные параметры сетевых графиков и их оптимизация……………40

Тема 4 Системы массового обслуживания…………………………………..44

§4.1 Марковские случайные процессы. Понятие системы массового обслуживания. Классификация систем…………………………………………...44

Тема 5 Теория игр……………………………………………………………….48

§5.1 Игровые модели. Платежная матрица. Нижняя и верхняя цена игры…….48

§5.2 Решение игр в смешанных стратегиях………………………………………52

Литература…………………………………………………………………………57

Тема 1 Линейное и целочисленное программирование.

§1.1 Общая постановка задачи линейного программирования. Классические задачи.

Общая задача линейного программирования формулируется следующим образом.

Даны система m линейных уравнений и неравенств с n переменными

и линейная функция .

Необходимо найти такое решение системы , где (j=1,2,…,l, l), при котором линейная функция F принимает оптимальное значение (т.е. максимальное или минимальное).

Записанная выше система называется системой ограничений, а функция F – линейной функцией, линейной формой, целевой функций или функцией цели.

Оптимальным решением (или оптимальным планом) задачи линейного программирования называется решение системы ограничений, удовлетворяющее условию неотрицательности переменных, при котором линейная функция F принимает оптимальное значение.

Каноническая задача линейного программирования имеет вид

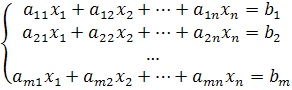, (j=1,2,…,l, l)

и линейная функция F .

Она отличается от других задач тем, что ее система ограничений является системой уравнений и все переменные неотрицательные.

При необходимости перехода от неравенства к уравнению вводятся дополнительные переменные. Неравенство заменяется уравнением и условием неотрицательности дополнительной переменной , а неравенство - уравнением . Дополнительные переменные вводят в целевую функцию с коэффициентом, равным нулю.

В канонической задаче целевая функция может как минимизироваться, так и максимизироваться. Для того чтобы перейти от нахождения максимума к нахождению минимума или наоборот, достаточно изменить знаки коэффициентов целевой функции. Полученная в результате этого задача и исходная задача имеют одно и тоже оптимальное решение, а значения целевых функций на этом решении отличаются только знаком.

Моделью будем называть условный образ какого-либо объекта, приближенно воссоздающий этот объект с помощью некоторого языка. В экономико-математических моделях таким объектом является экономический процесс, а языком – классические и специально разработанные математические методы.

Экономико-математическая модель – математическое описание исследуемого экономического процесса или объекта, которое выражает закономерности экономического процесса в абстрактном виде с помощью математических соотношений.

Для составления модели задачи линейного программирования, заданной в текстовой форме, необходимо:

1. ввести обозначение для неизвестных задачи

2. проанализировать ограничения для них (например, неотрицательность)

3. составить систему ограничений

4. составить целевую функцию и установить вид экстремума.

Этапы экономико-математического моделирования:

1. Постановка цели и задачи исследования. Качественное описание объекта в виде экономической модели.

2. Формирование математической модели, изучаемого объекта. Выбор или разработка методов исследования.

3. Анализ математической модели и полученных результатов.

Построение математических моделей простейших экономических задач.

1. Задача об использовании ресурсов (задача планирования производства)

Для изготовления двух видов продукции и используют четыре вида ресурсов, , и . Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице.

Вид ресурса	Запас ресурса	Число единиц ресурсов, затрачиваемых на изготовление единицы продукции
	18	1	3
	16	2	1
	5	-	1
	21	3	-

Прибыль, получаемая от единицы продукции и – соответственно 2 и 3 руб.

Необходимо составить такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

Решение.

Составим экономико-математическую модель.

Пусть и – число единиц продукции соответственно изапланированных к производству. Для их изготовления потребуется единиц ресурса , 2 единиц ресурса , , единиц ресурса и единиц ресурса .

Так как потребление ресурсов , и не должно превышать их запасов, соответственно 18,16,5 и 21 ед., то связь между потреблением ресурсов и их запасами выразится системой неравенств

По смыслу задачи переменные , .

Суммарная прибыль F составит руб. от реализации продукции и – от реализации продукции , т.е. .

Экономико-математическая модель задачи: найти такой план выпуска продукции , удовлетворяющий записанной системе неравенств при котором функция F принимает максимальное значение.

2. Задача составления рациона (задача о диете, задача о смесях).

Имеется два вида корма I и II, содержащих питательные вещества (витамины) , . Содержание числа единиц питательных веществ в 1 кг каждого вида корма необходимы минимум питательных веществ приведены в таблице.

Питательное вещество	Необходимый минимум питательных веществ	Число единиц питательных веществ в 1 кг корма
		I	II
	9	3	1
	8	1	2
	12	1	6

Стоимость 1 кг корма I и II соответственно равна 4 и 6 руб.

Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела.

Решение.

Составим экономико-математическую модель.

Пусть и – количество кормов I и II, входящих в дневной рацион. Тогда этот рацион будет включать 3 единиц питательного вещества , единиц питательного вещества , , единиц питательного вещества . Так как содержание питательных веществ , в рационе должно быть не менее соответственно 9, 8, и 12 единиц, то получим систему неравенств:

При этом переменные , .

Общая стоимость рациона F .

Экономико-математическая модель: составить дневной рацион , удовлетворяющий записанной выше системе с условием , , при котором функция принимает минимальное значение.