К задаче 6.6

	1	3	5	7
10	2	8	5	–	15
15	8	12	25	5	50
20	–	10	10	15	35
	10	10	40	20

Было произведено измерений, в каждом из которых измерялись две величины и. При большом числе измерений одно и то же значениеможет встретитьсяраз, одно и то же значение– раз, одна и та же пара чисел – раз. Поэтому данные наблюдений группируют, то есть подсчитывают частоты 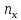,,. Сгруппированные данные записывают в виде так называемой корреляционной таблицы.

В первой строке таблицы указаны наблюдаемые значения переменной, а в первом столбце – наблюдаемые значенияпеременной. На пересечении строк и столбцов находятся частоты наблюдаемых пар значений переменных. Все частоты размещены в жирном прямоугольнике. Например, частота 12 указывает, что пара чисел наблюдалась 12 раз.

В последнем столбце записаны суммы частот строк. Например, сумма частот первой строки жирного прямоугольнике равна 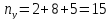, то есть значение переменной , равное 10 (в сочетании с различными значениями переменной), наблюдалось 15 раз.

В последней строк записаны суммы частот столбцов. Например, число 40 указывает, что значение переменной , равное 5 (в сочетании с различными значениями переменной), наблюдалось 40 раз.

В правой нижней клетке таблицы помещена сумма всех частот (общее число всех наблюдений). Очевидно, что .

В данном примере

, .

Составим корреляционную таблицу в условных переменных :

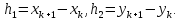
Выбрав (ложные нули), при, получим значениядля переменной,– для переменной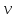. Корреляционная таблица в условных переменных примет вид:

	–2	–1	0	1
–1	2	8	5	–	15
0	8	12	25	5	50
1	–	10	10	15	35
	10	10	40	20

Вычислим и :

Находим вспомогательные величины:

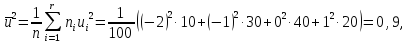
Находим выборочные среднеквадратические отклонения:

Коэффициент корреляции вычисляем по формуле

в которой все величины, кроме суммы, известны.

Для вычисления этой суммы составим расчетную таблицу:

	–2	–1	0	1
–1	2	8	5	–	–12	12
0	8	12	25	5	–23	0
1	–	10	10	15	5	5
	–2	2	5	15
	4	–2	0	15

В клетках последнего столбца записаны суммы произведений частот строки на соответствующие этим частотам значения переменной:. Например, число 12 получается суммированием произведений чисел в первой строке «жирного» прямоугольника на соответствующие значения переменной

Умножаем переменную на, и полученное произведение записываем в последнюю клетку той же строки, то есть в клетку столбца. Например, для первой строки,, следовательно,.

Сложив все числа столбца 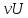, получим сумму, которая равна искомой сумме.

Для контроля аналогичные вычисления выполняют по столбцам. Сложив все числа в последней строке 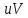, получим сумму которая при правильных вычислениях должна быть равна.

Искомая нами сумма:

Теперь вычисляем коэффициент корреляции:

Найдем остальные величины, входящие в уравнение регрессии:

В результате выборочное уравнение регрессии имеет вид

или окончательно