
- •Кафедра высшей математики
- •Содержание
- •Тематическое содержание рабочей программы по дисциплине «Математика» для специальности 2102 Математический анализ Кратные, криволинейные и поверхностные интегралы
- •Дифференциальные уравнения
- •Модели случайных процессов
- •Тематическое содержание рабочей программы по дисциплине «Математика» для специальности 0702 Математический анализ Кратные, криволинейные и поверхностные интегралы
- •Дифференциальные уравнения
- •Модели случайных процессов
- •Тематическое содержание рабочей программы по дисциплине «Математика» для специальностей 1706, 2713 Математический анализ Кратные и криволинейные интегралы
- •Обыкновенные дифференциальные уравнения
- •Теория вероятностей Элементарная теория вероятностей
- •Случайные величины
- •Математическая статистика Выборки и их характеристики
- •Элементы теории оценок и проверки гипотез
- •Статистические методы обработки экспериментальных данных
- •Указания по выполнению контрольных работ
- •Указания к решению задач контрольной работы №5
- •Указания к решению задач контрольной работы №6
- •К задаче 6.5
- •К задаче 6.6
- •Приложения
- •Список литературы
- •Для заметок
- •Математика
Теория вероятностей Элементарная теория вероятностей
Случайные события, виды событий. Классическое определение вероятности. Геометрическое определение вероятности.
Условная вероятность. Основные теоремы теории вероятностей. Формула полной вероятности. Формула Байеса. Повторные испытания. Формула Бернулли.
Случайные величины
Дискретные случайные величины. Закон распределения дискретной случайной величины. Функция распределения, ее свойства, график. Биномиальное распределение, распределение Пуассона, геометрическое распределение.
Непрерывные случайные величины. Плотность распределения случайной величины. Равномерное, нормальное, экспоненциальное распределения.
Математическое ожидание и дисперсия дискретной и непрерывной случайной величины, их свойства. Среднее квадратическое отклонение.
Предельные теоремы. Неравенство Чебышева. Закон больших чисел. Теорема Бернулли. Центральная предельная теорема.
Математическая статистика Выборки и их характеристики
Генеральная и выборочная совокупности, повторная и бесповторная выборки. Репрезентативная выборка. Статистическая функция распределения выборки. Статистический ряд. Гистограмма и полигон частот. Числовые характеристики статистического распределения.
Элементы теории оценок и проверки гипотез
Точечные и интервальные оценки математического ожидания и дисперсии. Метод наибольшего правдоподобия.
Статистические гипотезы. Математические методы проверки статистических гипотез. Основная и конкурирующая гипотезы, уровень значимости, ошибки первого и второго родов, критическая область, мощность критерия.
Статистические методы обработки экспериментальных данных
Дисперсионный анализ. Основные понятия дисперсионного анализа. Однофакторный дисперсионный анализ.
Корреляционный анализ. Основные понятия корреляционного анализа. Точечные оценки двумерной корреляционной модели. Проверка значимости генерального коэффициента корреляции. Интервальная оценка генерального коэффициента корреляции.
Регрессионный анализ. Основные понятия регрессионного анализа. Планирование регрессионного эксперимента. Обработка результатов активного эксперимента методом регрессионного анализа.
Указания по выполнению контрольных работ
По дисциплине «Математика» студенты II курса заочной полной и сокращенной форм обучения должны выполнить две контрольные работы – №5 и №6. Контрольные работы выполняются по следующим разделам и темам рабочей программы:
№5 – математический анализ: двойные интегралы, ряды и дифференциальные уравнения;
№6 – теория вероятностей и математическая статистика.
Ниже приведены варианты заданий контрольных работ. Индивидуальный номер варианта соответствует последней цифре номера зачетной книжки. Последняя цифра «0» соответствует десятому варианту.
Студенты специальностей 0702, 1706 и 2713 задания 5.4 и 5.5 контрольной работы №5 не выполняют.
Контрольная работа №5
Задача 5.1. Изменить порядок интегрирования в двойном интеграле. Сделать чертеж области интегрирования.
1.
 . 2.
. 2. .
.
3.
 . 4.
. 4. .
.
5.
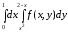 . 6.
. 6. .
.
7.
 . 8.
. 8. .
.
9.
 . 10.
. 10. .
.
Задача
5.2. Вычислить
объем тела, ограниченного указанными
поверхностями. Сделать рисунок данного
тела и его проекции на плоскость
 .
.
1.
 .
.
2.
 .
.
3.
 .
.
4.
 .
.
5.
 .
.
6.
 .
.
7.
 .
.
8.
 .
.
9.
 .
.
10.
 .
.
Задача 5.3.
В вариантах 1 – 4 найти координаты центра тяжести однородной фигуры, ограниченной линиями:
1.
 .
.
2.
 .
.
3.
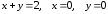 .
.
4.
 .
.
В вариантах 5 – 7 найти момент инерции относительно оси Oy однородной пластины, ограниченной линиями:
5.
 .
.
6.
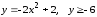 .
.
7.
 .
.
В вариантах 8 – 10 найти момент инерции относительно оси Ox однородной пластины, ограниченной линиями:
8.
 .
.
9.
 .
.
10.
 .
.
Задача 5.4. Исследовать на сходимость числовой ряд с помощью достаточных признаков сходимости.
1.
а)
 ; б)
; б) .
.
2.
а) ; б)
; б) .
.
3.
а)
 ; б)
; б) .
.
4.
а)
 ; б)
; б) .
.
5.
а)
 ; б)
; б) .
.
6.
а)
 ; б)
; б) .
.
7.
а)
 ; б)
; б) .
.
8.
а)
 ; б)
; б) .
.
9.
а)
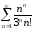 б)
б) .
.
10.
а)
 ; б)
; б) .
.
Задача 5.5. Найти область сходимости степенного ряда.
1.
 2.
2.
3.
 4.
4.
5.
 6.
6.
7.
 8.
8.
9.
 10.
10.
Задача 5.6. Найти частное решение дифференциального уравнения, удовлетворяющее начальному условию.
1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

Задача 5.7. Найти общее решение дифференциального уравнения.
1.
 2.
2.
3.
 4.
4.
5.
 . 6.
. 6.
7.
 8.
8.
9.
 10.
10. .
.
Задача 5.8. Найти частное решение дифференциального уравнения, удовлетворяющее начальным условиям.
1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

