Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет технологий и управления им. К.Г. Разумовского

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

II курс методички / Матаматика / математика ряды.doc

Скачиваний:

178

Добавлен:

20.04.2015

Размер:

1.49 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

Задания для самостоятельной работы

Разложить в ряд Фурье функцию с периодом .Изобразить график функции:

Разложить в ряд Фурье функцию с периодомв заданном интервале.Изобразить график функции:

1) ;

2) ;

3) ;

4) .

Разложить в ряд Фурье функцию 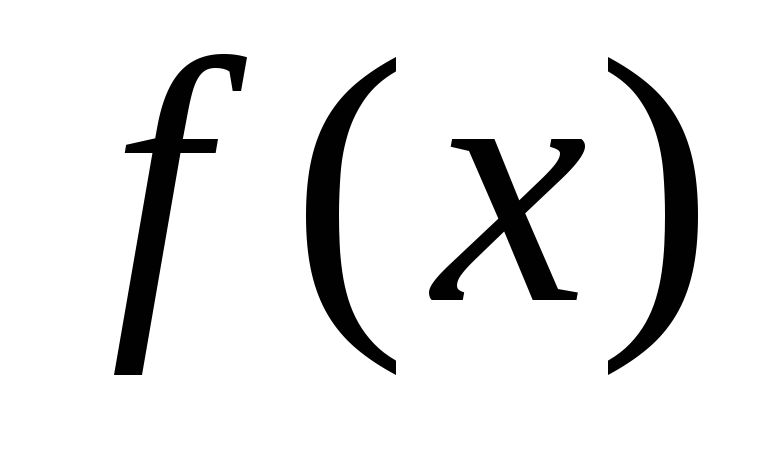с периодом в заданном интервале. Изобразить график функции:

1);

2) ;

3) ;

2) .

Разложить в ряд Фурье функцию в заданном интервале. Изобразить график функции:

1) ;

2) ;

3) .

Приложение 1. Числовые ряды

1	Числовой ряд:
2	n-я частичная сумма ряда:
3	Ряд сходящийся:
4	Необходимое условие сходимости ряда	Если ряд сходится, то сходимости ряда
5	Достаточное условие расходимости ряда
6	Геометрический ряд	, ряд сходится при , , ряд расходится при .
7	Гармонический ряд	, ряд расходящийся
8	Обобщенный гармонический ряд	, , ряд сходящийся при , ряд расходящийся при .
9	Знакоположительный ряд	,
10	Признаки сравнения для рядов (1) и (2),	а) , если ряд (2) сходящийся, то ряд (1) сходящийся; если ряд (1) расходящийся, то ряд (2) расходящийся б) если , то оба ряда сходящиеся, или оба ряда расходящиеся

Достаточные признаки сходимости для ряда ,
11	Признак Даламбера		, −ряд сходящийся, −ряд расходящийся, −дополнительное исследование
12	Радикальный признак Коши		, −ряд сходящийся, −ряд расходящийся, −дополнительное исследование
13	Интегральный признак Коши		, Сущ. такая, что , . Тогда интеграл сходящийся (или расходящийся) одновременно с данным рядом.
14	Знакопеременный ряд		, где − данные числа, как положительные, так и отрицательные
15	Знакочередующийся ряд
16	Признак Лейбница		Ряд сходится, если и .
18	Достаточный признак сходимости		Если ряд сходится, то сходится и ряд
19	Ряд абсолютно сходящийся		Если ряд сходящийся.
20	Ряд условно сходящийся		Если ряд сходящийся, а ряд расходящийся.

Приложение 2. Функциональные ряды. Степенные ряды

1	Функциональный ряд
2	n-я частичная сумма ряда
3	Сумма ряда
4	n-й остаток ряда
5	Степенной ряд	или , где − действительные числа
6	Радиус сходимости степенного ряда	или
7	Ряд Тейлора для функции
8	Ряд Маклорена для функции
Формулы разложения элементарных функций в ряд Маклорена
9	,
10
11	,
12	,
13	,
14	,
15	,
16	,
17	,

Приложение 3. Ряды Фурье

1	Ряд Фурье для периодической функции с периодом	, где , , ,
2	Ряд Фурье для четной периодической функции с периодом	, где , ,
3	Ряд Фурье для нечетной периодической функции с периодом	, где ,
4	Ряд Фурье для периодической функции с периодом	, где , , ,
5	Ряд Фурье для четной периодической функции с периодом	, где , ,
6	Ряд Фурье для нечетной периодической функции с периодом	, где ,