2.2. Задания для самостоятельной работы студентов
2.2.1. Вопросы для самоконтроля знаний студентов
Системы линейных уравнений и матрицы
Что называется матрицей размера
?Какая матрица называется квадратной; нулевой; диагональной; единичной?
Что называется суммой двух матриц; разностью, произведением числа
на матрицу А;
произведением матрицы А
на матрицу В?Выполняется ли переместительный закон по отношению к произведению двух матриц?
Перечислите свойства операций над матрицами.
Какая матрица называется транспонированной к данной матрице А?
Что называется дополнительным минором элемента матрицы n-го порядка?
Что называется алгебраическим дополнением элемента матрицы n-го порядка?
Какая матрица называется обратной по отношению к матрице А?
Сформулируйте необходимое и достаточное условие существования обратной матрицы.
Приведите формулу, с помощью которой находится обратная матрица.
Что называется рангом матрицы?
Какие преобразования матриц называются элементарными?
Какая система линейных уравнений называется линейной?
Что называется основной матрицей системы и расширенной?
Сформулируйте теорему Кронекера-Капелли – критерий существования системы линейных уравнений.
В каком случае система линейных уравнений имеет единственное решение; бесконечное множество решений; не имеет решений?
Опишите матричный метод решения невырожденных систем линейных уравнений.
Опишите правило Крамера решения невырожденных систем линейных уравнений.
Опишите метод Гаусса решения систем линейных уравнений
Векторная алгебра
Что называется вектором?
Какие векторы называются коллинеарными; компланарными?
Какие операции над векторами называются линейными?
Что называется суммой двух векторов; произведением вектора
на число 
.Что называется декартовой прямоугольной системой координат в пространстве?
Что называется радиус-вектором точки М относительно декартовой прямоугольной системы координат в пространстве?
Пусть в декартовой прямоугольной системе координат заданы точки
и 
.
Чему равны координаты вектора 
в этой системе координат?Что называется скалярным произведением двух векторов?
Перечислите свойства скалярного произведения векторов.
Как определяется проекция одного вектора на направление другого вектора?
Запишите формулу для вычисления длины вектора.
Как определяется скалярное произведение векторов через координаты векторов в декартовой системе координат?
Чему равен угол
между ненулевыми векторами 
и 
?В чем состоит условие ортогональности (перпендикулярности) векторов
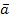и 
;
условие коллинеарности векторов 
и 
?Что называется векторным произведением двух векторов?
В чем состоит геометрический смысл модуля векторного произведения двух неколлинеарных векторов?
Перечислите свойства векторного произведения.
Запишите формулу для вычисления векторного произведения векторов
и 
.Что называется смешанным произведением трех векторов?
Каков геометрический смысл модуля смешанного произведения трех некомпланарных векторов?
В чем состоит необходимое и достаточное условие компланарности трех векторов?
Как выражается смешанное произведение трех векторов через координаты векторов в декартовой системе координат?
Аналитическая геометрия на плоскости
Запишите общее уравнение прямой на плоскости.
Какой геометрический смысл коэффициентов при x и y в общем уравнении прямой на плоскости?
Запишите уравнение прямой на плоскости, проходящей через точку
перпендикулярно вектору 
.Запишите каноническое уравнение прямой на плоскости и указать геометрический смысл входящих в него параметров.
Запишите уравнение прямой с угловым коэффициентом и указать геометрический смысл входящих в него параметров.
Уравнения каких прямых не могут быть записаны в виде уравнения с угловым коэффициентом?
Запишите условие параллельности и условие перпендикулярности двух прямых, заданных уравнениями
и 
.Запишите условие параллельности и условие перпендикулярности двух прямых, заданных уравнениям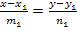и
и 
.Как найти расстояние от точки до прямой на плоскости?
Что называется эллипсом?
Запишите каноническое уравнение эллипса. Указать его оси симметрии, вершины и фокусы.
Что называется гиперболой?
Запишите каноническое уравнение гиперболы. Указать ее оси симметрии, вершины, фокусы, действительную ось, мнимую ось, асимптоты.
Что называется параболой?
Запишите каноническое уравнение параболы. Указать ее вершину, директрису, фокус, ось симметрии.
Что называется эксцентриситетом эллипса; гиперболы; параболы?
Запишите общее уравнение кривой второго порядка на плоскости. В каком случае это уравнение является уравнением эллиптического типа; гиперболического типа; параболического типа?
Аналитическая геометрия в пространстве
Запишите уравнение плоскости, проходящей через точку
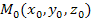перпендикулярно вектору 
.Запишите уравнение плоскости, проходящей через три точки.
С помощью какой формулы можно найти угол между плоскостями?
Запишите условие параллельности и перпендикулярности плоскостей
и 
.Как найти расстояние от точки до плоскости; от точки до прямой в пространстве?
Запишите канонические уравнения прямой в пространстве и указать геометрический смысл входящих в них параметров.
Запишите параметрические уравнения прямой в пространстве.
Запишите уравнение прямой в пространстве, проходящей через две данные точки
и 
.С помощью какой формулы можно найти угол между прямыми в пространстве?
Запишите условие параллельности и условие перпендикулярности прямых в пространстве, заданных в каноническом виде.
Как найти угол между прямой в пространстве и плоскостью?
Запишите условие параллельности и перпендикулярности прямой в пространстве и плоскости.
Какая поверхность называется цилиндрической?
Какая поверхность называется конической?
Какая поверхность называется поверхностью вращения?
Запишите общее уравнение поверхности второго порядка. Перечислите поверхности, которые может определять общее уравнение прямой.
Дискретная математика
Формулы перестановок, размещений, сочетаний и разбиений.
Формула бинома.
Полиномиальная формула.
Формулы включения и исключения.
Приложения к теории вероятностей.
Производящие функции.
Рекуррентные соотношения.
Перечисление классов эквивалентности.
Лемма Бернсайда.
Теорема Пойа.
Основные понятия теории графов.
Алгоритмы в дискретной математике.
Минимальное остовное дерево.
Кратчайший путь между двумя вершинами.
Задача коммивояжера.
Метод «ветвей и границ».
Паросочетания в двудольных графах.
Потоки в сетях.
Введение в анализ
Что называется функцией?
Что называется областью определения и множеством значений функции.
Какая функция называется монотонной; строго монотонной?
Дайте определение четной (нечетной) функции.
Что такое периодическая функция, период?
Перечислите основные элементарные функции.
Что называется пределом функции?
Определите понятие предела функции на бесконечности.
Сформулируйте определения односторонних пределов.
Сформулируйте первый замечательный предел; второй замечательный предел.
Что такое бесконечно малые функции? Перечислите их свойства.
Как сравнивают бесконечно малые функции?
Какие бесконечно малые функции называются эквивалентными?
Запишите цепочку эквивалентных бесконечно малых.
Что называется функцией, непрерывной в точке?
Что такое точки разрыва функции? Приведите классификацию точек разрыва функции.
Сформулируйте понятие непрерывности функции на отрезке.
Перечислите свойства функций, непрерывных на отрезке.
Дифференциальное исчисление функций одной переменной
Что называется производной функции?
В чем состоит геометрический и механический смысл производной?
Чему равна производная суммы, произведения и частного двух функций?
Запишите формулы дифференцирования степенной и показательной функции.
Что называется логарифмическим дифференцированием?
Как найти производную показательно-степенной функции?
Сформулируйте определение дифференциала. Какой его геометрический смысл?
Как используется дифференциал в приближенных вычислениях?
Сформулируйте определение производной n-го порядка.
Запишите формулу Лейбница для производной n-го порядка произведения функций.
Как найти производные первого и второго порядков функции, заданной параметрически; неявной функции?
Что называется дифференциалом n-го порядка?
Сформулируйте теорему Ролля. Укажите ее геометрический смысл.
Сформулируйте теорему Лагранжа. Укажите ее геометрический смысл.
Сформулируйте правило Лопиталя для раскрытия неопределенностей типа
и 
.Как раскрываются неопределенности типа
и 
с использованием правила Лопиталя?Как раскрываются степенные неопределенности с использованием правила Лопиталя?
Запишите формулу Тейлора с остаточным членом в форме Лагранжа.
Запишите формулу Маклорена.
Как найти интервалы возрастания и убывания функции?
Какое необходимое условие локального экстремума?
Какие точки называются критическими?
Сформулируйте достаточное условие существования экстремума функции, связанное с производной первого порядка.
Сформулируйте достаточное условие существования экстремума функции, связанное с производной второго порядка.
Как найти промежутки выпуклости, вогнутости, точки перегиба?
Как найти вертикальные асимптоты графика функции; наклонные асимптоты?
Как найти наибольшее и наименьшее значение функции на отрезке?
Дифференциальное исчисление функций нескольких переменных
Сформулируйте определение функции n переменных, ее области определения и множества значений.
Сформулируйте определение функции двух переменных и ее области определения. Каков геометрический смысл этих понятий?
Что называется линией уровня функции двух переменных?
Сформулируйте определение поверхности уровня функции
.Сформулируйте определение частных производных функции двух переменных.
Сформулируйте определение полного дифференциала функции n переменных; двух переменных.
Как используется полный дифференциал в приближенных вычислениях?
Сформулируйте определение производной по направлению.
Сформулируйте определение градиента функции.
Как связана производная по направлению с градиентом?
Определите и укажите правила нахождения производных и дифференциалов высших порядков.
Неопределенный интеграл
Дайте определение первообразной для функции f(x) на промежутке (a; b).
График какой первообразной для функции
пройдет через точку с координатами (1;
2π)?Поясните смысл операции «введение под знак дифференциала»?
Укажите правило применения замены переменной в неопределенном интеграле.
Запишите формулу интегрирования по частям.
Что обозначает термин «выделить целую часть неправильной дроби»?
На какие простейшие дроби раскладывается дробь
?Как рационализируется интеграл
?
Почему подстановка 
называется универсальной?Как вычисляется интеграл вида
в зависимости от четности и нечетности
показателей n и m?Как вычисляется интеграл вида
?При помощи каких подстановок можно вычислить интегралы
Определенный интеграл
Дайте определение определённого интеграла, укажите его геометрический смысл.
Перечислите основные свойства определённого интеграла.
Запишите формулу Ньютона-Лейбница.
Укажите правило применения замены переменной в определенном интеграле.
Выпишите формулу интегрирования по частям для определенного интеграла.
Дайте определение несобственного интеграла I рода и укажите его геометрический смысл.
Дайте определение несобственного интеграла II рода и укажите его геометрический смысл.
Сформулируйте признаки сходимости несобственного интеграла I рода.
Сформулируйте признаки сходимости несобственного интеграла II рода.
Как вычислить площадь плоской фигуры с помощью определенного интеграла?
Как вычислить длину дуги кривой в декартовой системе координат; в полярных координатах; в случае, если кривая задана параметрическими уравнениями?
Запишите формулу вычисления объёма тела по площадям его параллельных сечений.
Приведите формулу для объёмов тел вращений вокруг оси Ох, вокруг оси Оу.
Запишите формулу вычисления площади поверхности тела вращения.
Как найти массу неоднородного стержня?
По каким формулам находятся координаты центра тяжести плоской кривой и криволинейной трапеции?
Запишите формулу для вычисления работы переменной силы F(x).
Кратные, криволинейные и поверхностные интегралы
Дайте определение двойного интеграла.
Приведите примеры области D, для которой не существует двойного интеграла.
Какая область называется правильной в направлении оси Ох и в направлении оси Оу?
Как вычислить двойной интеграл?
Каковы пределы интегрирования для области D, являющейся прямоугольником?
Запишите общую формулу замены переменной в двойном интеграле.
Какие координаты называются обобщёнными полярными координатами? Чему равен для таких координат якобиан?
Дайте определение тройного интеграла и сформулируйте условия существования тройного интеграла.
Как вычислить тройной интеграл в прямоугольных координатах; в цилиндрических координатах; в сферических координатах?
Как вычислить площадь замкнутой ограниченной области с помощью двойного интеграла?
Какую фигуру можно назвать криволинейным цилиндрическим телом, и как при помощи двойного или тройного интеграла вычислить его объём?
Как вычислить массу пластины и тела, если известна поверхностная или объёмная плотность в каждой точке?
Что называется криволинейным интегралом I рода?
Как вычислить криволинейный интеграл I рода с помощью определённого интеграла, если уравнение кривой интегрирования задано в виде у=у(х) или х=х(у)?
Как с помощью криволинейного интеграла I рода вычислить длину дуги и массу кривой?
Что называется криволинейным интегралом II рода?
Как вычислить криволинейный интеграл II рода с помощью определённого интеграла?
Напишите и формулу Грина.
Сформулируйте условия независимости криволинейного интеграла II рода от формы кривой – пути интегрирования.
Как найти функцию двух или трёх переменных по их полному дифференциалу?
Как с помощью криволинейного интеграла II рода вычислить площадь плоской фигуры?
Как вычислить работу переменной силы при перемещении материальной точки вдоль данной кривой?
Что называется поверхностным интегралом I рода и как он вычисляется?
Какие применения имеет поверхностный интеграл I рода?
Как найти массу материальной поверхности при помощи поверхностного интеграла I рода?
Что называют поверхностным интегралом II рода и как он вычисляется?
В чём заключается разница и какая связь между поверхностными интегралами I и II рода?
Напишите формулу Остроградского-Гаусса.
Запишите формулу Стокса.
Дифференциальные уравнения
Какое уравнение называется дифференциальным уравнением первого порядка?
Дайте определение общего и частного решений дифференциального уравнения первого порядка.
Сформулируйте теорему Коши существования и единственности решения дифференциального уравнения первого порядка.
Запишите общий вид дифференциального уравнения с разделяющимися переменными.
Какое дифференциальное уравнение первого порядка называется однородным?
Запишите общий вид линейного дифференциального уравнения первого порядка.
Какие методы решения линейного дифференциального уравнения первого порядка вы знаете?
Запишите уравнение Бернулли и укажите методы его решения.
Сформулируйте необходимое и достаточное условие того, чтобы уравнение P(x,y)dx+Q(x,y)dy=0 было уравнением в полных дифференциалах.
Какие способы решения уравнения в полных дифференциалах существуют?
Что такое интегрирующий множитель?
Дайте определение дифференциального уравнения n-ого порядка.
Что называется общим и частным решениями дифференциального уравнения n-ого порядка?
Какие типы дифференциальных уравнений высших порядков допускают понижение порядка?
Какие дифференциальные уравнения n-ого порядка называют линейными однородными ; неоднородными? Запишите их в общем виде.
Какая система решений линейных однородных дифференциальных уравнений называется фундаментальной?
Как записывается общее решение линейных однородных дифференциальных уравнений n-ого порядка?
Как записывается общее решение линейных неоднородных дифференциальных уравнений n-ого порядка?
В чём заключается метод вариации произвольных постоянных?
В чём заключается принцип суперпозиции решений для линейных неоднородных дифференциальных уравнений n-ого порядка?
Какое уравнение называют характеристическим? Как его найти?
Какой вид имеет общее решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами , если корни характеристичекого уравнения:
а) действительные и различные;
б) равные;
в) комплексные;
Какие специальные виды правой части линейного неоднородного дифференциального уравнения n-ого порядка с постоянными коэффициентами рассматриваются при подборе вида частного решения?
Запишите частное решение линейного неоднородного дифференциального уравнения n-ого порядка для случаев, когда правая часть f(x) имеет вид:
а)
б)
в)
Какая система дифференциальных уравнений называется канонической; нормальной?
Сформулируйте задачу Коши для нормальной системы дифференциальных уравнений.
Что называется общим решением нормальной системы дифференциальных уравнений?
Запишите линейную однородную систему дифференциальных уравнений.
Какова структура общего решения линейной однородной системы дифференциальных уравнений?
Запишите линейную неоднородную систему дифференциальных уравнений.
Какова структура общего решения линейной неоднородной системы дифференциальных уравнений?
Теория функций комплексной переменной
Дайте определение комплексной переменной.
Какая функция называется однозначной, многозначной?
Перечислите основные элементарные функции комплексной переменной.
Дайте определение тригонометрических функций. Перечислите их свойства.
Дайте определение гиперболических функций. Перечислите их свойства.
Как определяется логарифмическая функция? Что называется главным значением этой функции?
Запишите обратные тригонометрические функции.
Запишите обратные гиперболические функции.
Дайте определение предела функции в точке.
Дайте определение функции, непрерывной в точке; непрерывной в области.
Дайте определение дифференцируемой функции комплексной переменной.
Что называется производной функции?
Запишите условие Коши-Римана.
Запишите уравнение Лапласа.
Какая функция называется аналитической?
Какая функция называется гармонической?
В чем заключается геометрический смысл модуля производной?
Какой геометрический смысл аргумента производной?
Что называется конформным отображением?
Дайте определение интеграла функции комплексной переменой вдоль кривой С.
Приведите формулу, сводящую вычисление интеграла функции комплексной переменной к вычислению криволинейных интегралов II рода функции действительных переменных.
Запишите формулу для вычисления интеграла функции комплексной переменной вдоль кривой С в случае задания кривой параметрическими уравнениями.
Запишите формулу Ньютона-Лейбница для вычисления интеграла функции комплексной переменной. При каких условиях она имеет место?
Запишите интегральную формулу Коши. Как она используется при вычислении интегралов?
Сформируйте основную теорему Коши; обобщенную теорему Коши.
Что называется вычетом функции?
Чему равен вычет в устранимой особой точке?
Как вычислить вычет в полюсе?
Как вычислить вычет в существенно особой точке?
Чему равен вычет для n-кратного полюса?
Сформулируйте теорему Коши о вычетах. Как она применяется для вычисления интегралов?
Дайте определение функции-оригинала.
Что называется изображением функции-оригинала?
Дайте определение преобразования Лапласа.
Какая функция называется единичной, что является ее изображением?
Чему равно изображение функции
.Сформируйте свойство линейности преобразования Лапласа.
Приведите таблицу изображения основных функций.
Как находится изображение по заданному оригиналу?
Как находится оригинал по его изображению?
Теория вероятностей
Какие события называются достоверными, невозможными, случайными?
Какие события называются совместными, несовместными, равновозможными?
Как обозначают и в каких случаях используют классическое и геометрическое определение вероятности?
Какие основные свойства вероятности?
Какие комбинации называются перестановками, размещениями, сочетаниями? Как обозначается и вычисляется количество этих соединений?
Сформулируйте теоремы сложения вероятностей совместных и несовместных событий.
Какие случайные события называются независимыми?
Как обозначают и определяют условную вероятность?
Сформулируйте и запишите теоремы умножения вероятностей зависимых и независимых случайных событий?
Каким условиям должно удовлетворять событие, чтобы его вероятность можно было найти по формуле полной вероятности? Какой вид имеет эта формула?
Применение формулы Байеса. Запишите формулы Байеса.
Что называется формулой Бернулли?
По каким формулам находят вероятность появления события А менее m или не менее m раз в n независимых испытаниях схемы Бернулли?
По какой формуле находят вероятность появления события А хотя бы один раз в n испытаниях?
Как найти наиболее вероятное значение числа появления события А в схеме Бернулли?
В каких случаях используют формулу Пуассона, локальную или интегральную формулы Муавра-Лапласа?
Как найти вероятность появления события в случае простого потока?
Что такое случайные величины, дискретные и непрерывные случайные величины?
Укажите основные законы распределения дискретной величины и условия их использования.
Как определяются и что характеризуют числовые характеристики дискретных случайных величин?
Как определяют функцию распределения и плотности вероятностей непрерывных случайных величин? Какие свойства имеют эти функции?
Какая существует связь между интегральной и дифференциальной функциями распределения вероятностей?
По каким формулам можно вычислить вероятность попадания случайной величины в промежуток
,
используя интегральную или дифференциальную
функции распределения?Какие числовые характеристики существуют для непрерывных случайных величин и что характеризует каждая из них?
Как вычислить числовые характеристики непрерывных случайных величин?
Укажите основные свойства математического ожидания и дисперсии.
Укажите основные законы распределения непрерывных случайных величин и их вид.
Каковы числовые характеристики основных законов распределения дискретных и непрерывных случайных величин?
По каким формулам находят вероятность попадания случайной величины X в промежуток
,
если X распределена по равномерному,
показательному или нормальному закону?Как найти функцию распределения
,
если X – дискретная или непрерывная
случайная величина?Как определяют начальные и центральные моменты, коэффициент корреляции и как связаны понятия корреляции, зависимости и независимости случайных величин?
Сформулируйте правило
и как оно используется?Сформулируйте центральную предельную теорему Ляпунова.
Математическая статистика
Что является предметом математической статистики?
Сформулируйте основные задачи математической статистики.
Дайте определения генеральной и выборочной совокупности.
Охарактеризуйте сущность выборочного метода в математической статистике.
Дайте определения дискретного и интервального вариационных рядов.
Что называется эмпирической функцией распределения.
Что называется полигоном и гистограммой?
Дайте определения выборочной средней, выборочной дисперсии, выборочного среднеквадратического отклонения.
Дайте определение точечной оценки параметров распределения случайной величины и сформулируйте требования, предъявляемые к точечным оценкам.
Укажите точечные оценки математического ожидания и дисперсии.
Охарактеризуйте метод моментов получения точечных оценок.
Охарактеризуйте метод максимального правдоподобия.
Дайте определения доверительного интервала, доверительной вероятности, укажите точность оценки.
Укажите правило построения доверительного интервала для оценки математического ожидания нормального распределения при известной дисперсии.
Укажите правило построения доверительного интервала для оценки математического ожидания нормального распределения при неизвестной дисперсии.
Укажите правило нахождения интервальной оценки среднеквадратического отклонения нормального распределения.
Дайте определение статистической гипотезы, основной и альтернативной гипотез.
Дайте определения ошибок первого и второго рода, критической области.
Назовите основные этапы проверки статистических гипотез.
Сформулируйте правило проверки гипотезы о значении математического ожидания нормального распределения.
Сформулируйте правило проверки гипотезы о нормальном распределении с использованием критерия Пирсона.