Контрольные вопросы.

1. Каковы основные свойства определителей?

2. Что называется минором и алгебраическим дополнением?

3. Каковы способы вычисления определителей?

Тест 1.

Вычислить определители и указать верный ответ

а)

б)

а)

б)

1.3. Решение систем линейных уравнений (метод Крамера).

Рассмотрим систему двух линейных уравнений с двумя неизвестными

(1.6)

Составим из коэффициентов при неизвестных и свободных членов три определителя и (1.7)

Решениемсистемы называется совокупность чисел, которые, будучи подставлены вместо неизвестных в уравнения, обращают эти уравнения в тождества. Система уравнений называетсясовместной, если она имеет хотя бы одно решение, инесовместной,если не имеет ни одного решения.

Совместная система называется определённой,если она имеет только одно решение, инеопределённой, если она имеет более одного решения.

Легко видеть, что второй и третий определители получаются из первого заменой столбца соответствующих индексу коэффициентов столбцом свободных членов. Правило Крамера решения системы линейных уравнений заключается в использовании соотношений ; (1.8) Отметим, что использовать их можно при∆ ≠ 0. Это тот случай, когда системаопределенаисовместна(т.е. имеетединственное решение).Если∆ = 0, а хотя бы один из определителей∆_x, ∆_yотличен от нуля((∆_x)²+(∆_y)² ≠ 0), то системанесовместна(т.е.не имеет решений), а если = ∆_x = ∆_у = 0, то системанеопределенаи имеетбесконечное множество решений.

Аналогично правило Крамера формулируется и для системы из трех (или n) линейных уравнений с тремя (илиn) неизвестными.

(1.9) (1.8') (1.7')

А _x, _y, _zполучаются иззаменой столбца соответствующих коэффициентов столбцом свободных членов. Аналогично проводится и исследование системы (возможны те же три случая).

Если свободный член (правая часть) линейного уравнения равен нулю- уравнение называется однородным. Однороднойназывают и систему таких уравнений (система (1.9) приd₁=d₂=d₃=0). При 0она имеет единственное решение (x=y=z=0), называемоетривиальным. Если же=0, то система сводится либо к двум , либо к одному уравнению с тремя неизвестными. В этих случаях однородная система имеет бесконечное множествонетривиальныхрешений.

Если (1.6) сводится (при d₁=d₂=d₃=0) к двум линейным уравнениям, решения системы можно найти по формулам:

(1.10)

где может принимать любые значения.

Контрольные вопросы.

1. Какой вид имеют формулы Крамера и в каком случае они применяются?

2. При каком условии система линейных уравнений имеет единственное решение?

3. При каком условии система n линейных однородных уравнений с n неизвестными имеет ненулевое решение?

Тест 2.

Решить с помощью определителей системы уравнений и указать верные ответы:

1)

1. а) ; б);

2)

2. а) ; б).

1.4. Матрицы. Основные свойства и операции.

Матрицейназывают прямоугольную таблицу, составленную из каких – либо математических объектов (элементов), в простейшем случае – из чисел. Принятое обозначение:

В общем случае числа строк mи столбцовnпроизвольны и определяютразмерматрицы, обозначаемый (mn). Если строка одна,А = (а₁₁, а₁₂, …, а_1n)–матрица-строка; аналогично определяетсяматрица–столбец(размеры – (1n) и (m1) соответственно).

Если число строк равно числу столбцов – квадратная матрица порядкаn. Квадратной матрицеАсоответствует определитель, обозначаемый_А(илиD_А). Если_А  0, матрицаАназываетсяневырожденной (неособой), если_А = 0, тоА–вырожденная (особая)матрица.

Если в квадратной матрице Апоменять местами столбцы и строки, то получим новую матрицу, обозначаемуюА*и называемуютраспонированной(сама операция замены называется траспонированием). Квадратная матрица, у которой все элементы (кроме, может быть, стоящих поглавной диагонали, идущей из левого верхнего в правый нижний угол) равны нулю, называетсядиагональной. Такая матрица, если все диагональные элементы равны единице, называетсяединичнойи обозначается буквойЕ.Нулевойназывают матрицу, все элементы которой равны нулю.

Квадратную матрицу, в которой а_ij = a_jiназываютсимметрической(такая матрица совпадает со своей транспонированной, т.е.А = А*).

Две матрицы АиВсчитаются равными(А = В)тогда и только тогда, когда равны их соответственные элементы, т.е. а_mn = b_mn.

Матрицы одинакового размераможно складывать, получая новую матрицу того же размера по формуле:

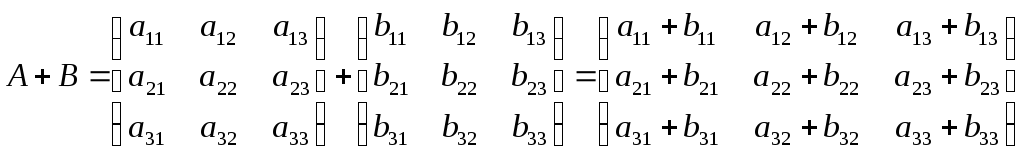(1.11)

Произведением числа  на матрицуАназывают матрицу определяемую

равенством: (1.12)

Умножение матрицвозможно в том случае, если число столбцовумножаемойматрицы равно числу строк матрицы множителя. Размер матрицы-произведения определяется соотношением (mn)(nk)=(mk). Произведение матрицАиВ, обозначаемоеАВнаходят по правилу:

(1.13)

т.е. элемент матрицы – произведения, стоящий в i– й строке ик– ом столбце, равен сумме произведений соответственных элементовi– й строки матрицыАик– ого столбца матрицыВ. Пример:

Отметим, что переместительный закон для произведения матриц вобщем случаене выполняется:АВ  ВА.

Аналогично понятию обратного числа (произведение числа на число обратное равно единице: а  а^–1 = 1) вводится понятие обратной матрицыА^–1.

А  А^–1 = Е, гдеЕ– единичная матрица.

Обратную матрицу имеет всякая невырожденная квадратная матрица, причем:

где А_mn– алгебраическое дополнение элемента матрицыа_mn(см. (1.4.))

Альтернативный способ вычисления А^-1приведён в разделе (1.4.3)