Лабораторная работа 3. Анализ формы распределения данных и расчет показателей центральной тенденции рядов распределения в ms Excel

В MS Excel есть возможность анализа формы рядов распределения и расчета показателей их центральной тенденции (среднего значения, моды, медианы, экстремумов (максимального и минимального значений)). Для их вычисления применяются статистические функции и инструмент Анализ данных.

Ряды распределения строятся с целью изучения состава исследуемой совокупности, ее однородности, колеблемости значений признаков и границ их изменения. На основе рядов распределения рассчитываются относительные величины структуры и средние показатели.

Ряд распределения в статистике  это ряд цифровых показателей, представляющих распределение единиц совокупности по одному существенному признаку, значения которого расположены в определенной последовательности.

Ряд распределения включает два элемента:

1. варианты (х)  отдельные возможные значения признака;

2. частоты или веса (f) – это численность отдельных групп, т.е. числа, которые показывают, сколько раз данное значение признака встречается в исследуемой совокупности.

Правила построения ряда распределения аналогичны правилам построения группировки. Но иногда при наличии достаточно большого количества вариантов значений признака ряд распределения является трудно обозримым и непосредственное рассмотрение его не дает представления о распределении единиц по значению признака в совокупности. Поэтому первым шагом в упорядочении первичного ряда является его ранжирование, т.е. расположение всех вариантов в возрастающем (или убывающем) порядке.

При проведении эмпирического исследования ряда распределения рассчитываются и анализируются следующие группы показателей:

• показатели формы распределения;

• показатели положения центра распределения;

• показатели степени его однородности.

Для анализа формы рядов распределения чаще всего используют их графическое изображение. Для изображения рядов применяются линейные графики и плоскостные диаграммы, построенные в прямоугольной системе координат.

В статистике выделяют две формы распределения данных: нормальную и несимметричную.

Нормальное распределение (термин был впервые введен Гальтоном в 1889 г.), иногда называемое гауссовским, можно представить в виде симметричной кривой в форме колокола (рис. 3.1). Такая кривая представляет идеальный набор данных, что редко встречается на практике.

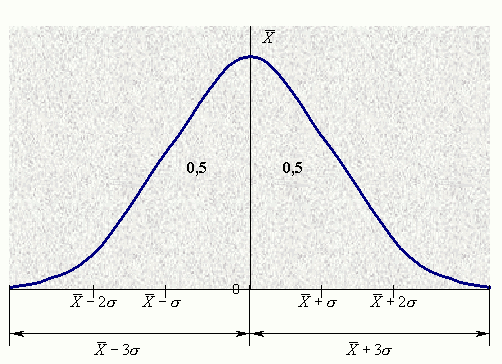
Рис. 3.1. Кривая нормального распределения

Тем не менее, нормальное распределение играет большую роль в статистике. С помощью графического изображения статистических данных важно определить, являются ли данные нормально распределенными, т.к. только в случае распределения близкого к нормальному можно использовать стандартные статистические процедуры, в противном случае полученные результаты анализа данных могут быть неточными или неверными.

На практике же чаще всего встречаются несимметричные формы распределения. Для решения этой проблемы в статистике используют специальное преобразование, которое переводит несимметричное распределение в более симметричное. Наиболее распространенным типом преобразования данных в экономике является логарифмирование, которое заключается в замене каждого значения ряда данных его десятичным или натуральным логарифмом.

В статистике могут встречаться одновершинные и многовершинные кривые распределения.

Однородные совокупности описываются одновершинными распределениями, а многовершинность распределения свидетельствует о неоднородности изучаемой совокупности или о некачественном выполнении группировки.

Одновершинные кривые распределения делятся на симметричные, умеренно асимметричные и крайне асимметричные.

К показателям положения центра распределения относятся степенная средняя (средняя арифметическая) и структурные средние – мода и медиана.

Мода и медиана являются дополнительными к средней величине характеристиками совокупности, по ним также можно судить о форме рядов распределения.

Если значение средней величины совпадает с модой и медианой, то ряд является симметричным. На практике строго симметричные ряды встречаются довольно редко, чаще исследователю приходится иметь дело с асимметричными рядами.

Для характеристики асимметрии используют коэффициенты асимметрии.

Простейшим показателем асимметрии может служить разность между средней арифметической величиной и модой.

Если AS = <0, то в ряду имеет место правосторонняя асимметрия, если AS = >0, то – левосторонняя.

Для симметричных распределений может быть рассчитан показатель эксцесса, который показывает, насколько резкий скачок имеет изучаемое явление.

Если показатель эксцесса больше нуля, то распределение островершинное и скачок считается значительным, если коэффициент эксцесса меньше нуля, то распределение считается плосковершинным и скачок считается незначительным.

Однородность статистических совокупностей характеризуется величиной вариации (рассеяния) признака, т.е. несовпадением его значений у разных статистических единиц. Для измерения вариации в статистике используются абсолютные и относительные показатели.