5.3. Теория массового обслуживания.

1. Часто приходится сталкиваться с системами, предназначенными для многоразового использования при решении схожих задач. возникающие при этом процессы получили названия процессов обслуживания, а системы – систем массового обслуживания (СМО).

• Случайный процесс, протекающий в системе, называется Марковским, если для любого момент времени t_o вероятностные характеристики процесса в будущем зависит только от его состояния в данный момент t_o и не зависит от того, когда и как система пришла в это состояние.

• Потоком событий называется последовательность однородных событий, следующих одно за другим в какие-то случайные моменты времени.

• Интенсивность потока λ – среднее число событий приходящиеся на единицу времени.

Интенсивность потока может быть как постоянной, так и переменной, зависящей от времени.

Для простейшего потока с интенсивностью λ интервал Т между соседними событиями имеет показательное распределение с плотностью: f(t)= λe^{- λt}, t > 0.

2. Рассмотрим математическую модель изменения численности популяции – процесс гибели и размножения. Граф состояний процессы гибели и размножения представлен на рис.8.

Найдём все финальные вероятности системы.

Рассмотрим упорядоченное множество состояний системы S₀, S₁, …, S_n. Из любого состояния переходы могут осуществляется только в состоянии с соседними номерами. Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями. Тогда для первого состояния S₀ имеем: λ₀₁p₀= λ₁₀p₁ (*)

Для второго состояния S₁: (λ₁₂+λ₁₀)p₁= λ₀₁p₀ + λ₂₁p₁

В силу (*) имеем: λ₁₂p₁= λ₂₁p₂.

Далее, записывая уравнения для предельных вероятностей других состояний, получается система:

λ₀₁p₀= λ₁₀p₁

λ₁₂p₁= λ₂₁p₂

_{. . . . . . . .}

λ_{n-1 n} p_n-1= λ_{n n-1} p_n

Учтем нормировочное условие: p₀+ p₁+…+p_n =1

Решим систему уравнений:

p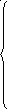₁= p₀

p₂= p₁= p₀

. . . . . . . .

p_n= p₀

Подставляя равенства в нормировочное условие, получаем

P ₀ = (1+ + +… + )^-1

3. Рассмотрим любую систему массового обслуживания и связанные с него два потока событий: поток заявок, прибывающих в СМО, и поток заявок, покидающих СМО. Если в системе устанавливается стационарный режим, то среднее число заявок, прибывающих в СМО за единицу времени, равно среднему числу заявок, покидающих ее: оба потока имеют одну и ту же интенсивность.

Пусть, Х(t) – число заявок, прибывших в СМО до момента t; Y(t) – число заявок покинувших СМО до момента t.

Обе функции являются случайными и меняются скачком в моменты переходов и уходов заявок. Функция Z(t)=X(t)-Y(t) – число заявок, находящихся в очереди. Рассмотрим очень большой промежуток времени Т и вычислим для него среднее число заявок, находящихся

в СМО:

Этот интеграл представляет собой площадь фигуры состоящей из прямоугольников, каждый из которых имеет высоту, равную единице, и основание, равное времени пребывания в системе соответствующей заявки. Обозначим эти времена t₁, t₂,… .

Таким образом, при достаточно больших Т, можно считать что

, где сумма распространяется на все заявки, пришедшие за время Т.

Тогда,L _сист = t_i =  t_iλ

Величина Tλ есть среднее число заявок, пришедших за время Т. Если разделить сумму всех времен t_i на среднее число заявок, то получится среднее время пребывания заявки в системе W_сист.

Получаем, что L_сист = λW_сист

Откуда. W_сист = L_сист – формула Литтла.

Таким же образом получается вторая формула Литтла: среднее время пребывания заявки в очереди равно отношению среднего числа заявок в очереди к интенсивности потока заявок:

4. Пусть имеется одноканальная СМО с очередью.

Предположим, что на очередь не наложено никаких либо ограничений (по длине, по времени ожидания).

На СМО поступает поток заявок с интенсивностью λ; поток обслуживаний имеет интенсивность , обратную среднему времени обслуживания заявки t_об. Найдем финальные вероятности состояний СМО, а также характеристики ее эффективности: Lсист (среднее число заявок в системе), Wсист (среднее время пребывания заявки в очереди), L_or (среднее число заявок в системе), W_or (среднее время пребывания заявки в очереди), P_зан (вероятность того, что канал занят).

Абсолютная пропускная способность А СМО равна интенсивности потока заявокλ в силу того, что очередь неограниченна и все заявки будут обслужены. Откуда относительная пропускная способность СМО равна единице.

рис.9.

Состояния системы: S_o – канал свободен;

S₁ – канал занят, очереди нет;

S₂ – канал занят, одна заявка;

…

S_n – канал занят, n-1 заявок

Схема СМО с неограниченной очередью есть схема гибели и размножения с бесконечным числом состояний. Финальные вероятности для такой СМО существуют только тогда, когда система не перегружена (ρ < 1). Если приведенная интенсивность потока заявок больше либо равно единице (ρ ≥ 1), при t → ∞ очередь неограниченно растет.

Ряд в формуле представляет сбой геометрическую прогрессию и при ρ < 1 сходится

, , … ,

Вероятности образуют геометрическую прогрессию. Самое вероятное состояние – канал свободен.

Найдем среднее число заявок в очереди

По формуле Литтла:

По правилу сложений математических ожиданий среднее число заявок в очереди равно разности среднего числа заявок в системе и их среднего обслуживанием. Число заявок под обслуживанием может быть либо нулем, либо единицей. Причем вероятность такой случайной величины равно вероятности того, что канал занят.

, ,

По формуле Литтла:

5. Рассмотрим многократную СМО с неограниченной очередью.

Состояния системы: S_o – все каналы свободны;

S₁ – занят один канал;

S₂ – занято два канала;

S_n – все каналы заняты;

S_n+1 – заняты все каналы, одна заявка в очереди;

S_{n + r} – заняты все каналы, r заявок в очереди.

Рис10

Финальные вероятности существуют, если В противном случае очередь растет до бесконечности.

Пусть

, , … , , , … ,

Среднее число занятых каналов:

Замечания: Допущение при котором анализировались рассмотрение выше СМО.

Состоит в том, что все потоки событий, переводящие их из состояния в состояние, были простейшими. При нарушении этого требования общих аналитических методов для таких систем не существует.