Магнитный момент атома. Мы говорили о гиромагнитном отношении (глава 6, §2, формула (1))

; 

(13)

Проекция на направлениеz

Ряд опытных фактов говорит о

(14)

Вследствие удвоенного магнетизма спина гиромагнитное отношение полных моментовиоказывается функцией квантовых чиселL, S иJ. Числа L и S - характеризуют отношение значенийи,а числоJ – определяет взаимную ориентацию орбитального и спинового моментов.

Соответствующий квантово-механический расчет для магнитного момента атома дает формулу

, где (15)

, назыв. множителем или фактором Ланде. (16)

Если S=0, J=L получаем формулу (13)

g=1

Если L=0 (J=S) g=2, получаем формулу (14)

Отметим, что множитель Ланде может иметь значения, меньшие единицы и даже может быть равен нулю (это получается, например, при L=3, S= 2, J=1) . В этом случае магнитный момент атома равен нулю, хотя механический момент отличен от нуля.

Наличие «-» в формуле (15) позволяет получить проекцию на ось z заменойна:

(17)

Состояния атомовусловно обозначаются символом, называемымтермом.

L 0 1 2 3 4 5 6

S P D F G H I

Терм содержит сведения о значениях трех квантовых чисел L, S, J.

Термы с наименьшей энергией (основные) определяются двумя эмпирическими правилами Хунда.

1. Из термов данной электронной конфигурации наименьшей энергией обладает терм с наибольшим значением S и с наибольшим возможным при такомS значенииL. Эти условия обеспечивают минимизацию кулоновского отталкивания электронов в атоме.

2. Для терма в основном состоянии , если подоболочка заполнена менее, чем наполовину иJ=L+S – в остальных случаях, что соответствует минимуму энергии спин-орбитального взаимодействия.

Существуют ограничения на квантовые числа начального и конечного состояний, при которых возможны переходы. Они называются правилами отбора.

(выше говорилось о правилах отбора для азимутального и.( см. формулу (9)) квантовых чисел).

Для других чисел

:

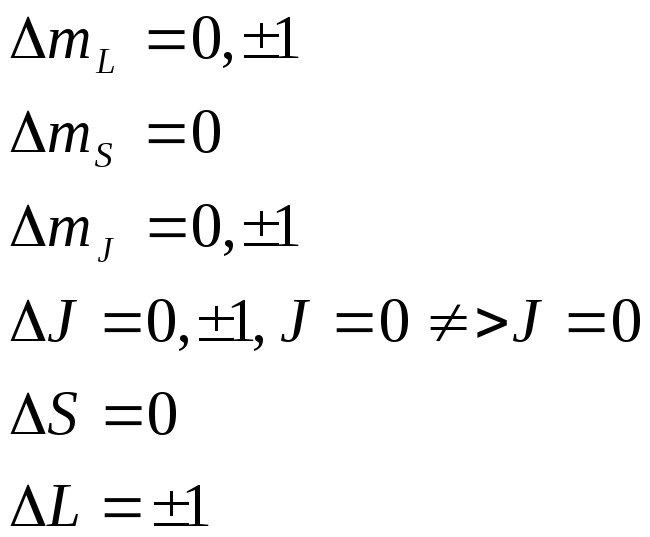
Примеры

Задача 1 (И. Е. Иродов, № 6.160, )(№5.206-нов.)

Некоторый атом находится в состоянии, для которого S=2, полный механический момент , а магнитный момент=0. Написать спектральный символ соответствующего терма.

Решение:

L 0 1 2 3

S P D F Ответ:

Задача 2 (И. Е. Иродов, № 6.122)(5.175-нов.)

Установить, какие из нижеперечисленных переходов запрещены правилами отбора.

;

L=2 L=1

J=3/2 J=1/2

S=1/2 S=1/2

Переход запрещен.

Переход разрешен